PCA of Waimea Wave Climate By Kjersti Johnson

Do the variables that affect wave climate exhibit significant relationships with each other? Are there continuous patterns/environmental gradients in Waimea swell data? • The goal of this project is to investigate trends in characteristics of oceanic wave climate data. • A Principal Component Analysis (PCA) will help to determine if significant relationships among environmental variables exist and which of these variables exhibit the strongest covariation • My hypothesis was that significant wave height and mean wave period will exhibit the strongest covariance in the data. Generally speaking, a longer wave period indicates larger waves. Therefore, these variables could very likely be the principal components.

Dataset Obtained from PACIOOS (Pacific Islands Oceans Observing System) • • Main Matrix: Variables (n=4): 1) Significant Wave Height (ft) 2) Peak Wave Period (seconds) 3) Mean Wave Period (seconds) 4) Mean Wind Speed (mph) All main matrix variables are quantitative 61 Samples – (Each day of December 2017 and January 2018) Peak swell season

Data Processing Assumptions of normality/linearity Overall, the skewness looks adequate. Acceptable skewness range is -1 to 1 (Significant wave height is the only variable that is barely out of range) Percentage of empty cells is very low (0. 82%) There were no outliers! All variables were within 2 standard deviations of the mean Therefore, I did not discard any samples or variables. Although the dataset was normal, the variables are still in different units (seconds, feet, and miles per hour). The column sums are not relatively equal so I chose to do a general relativization by column to give each variable an equal weight in the analysis.

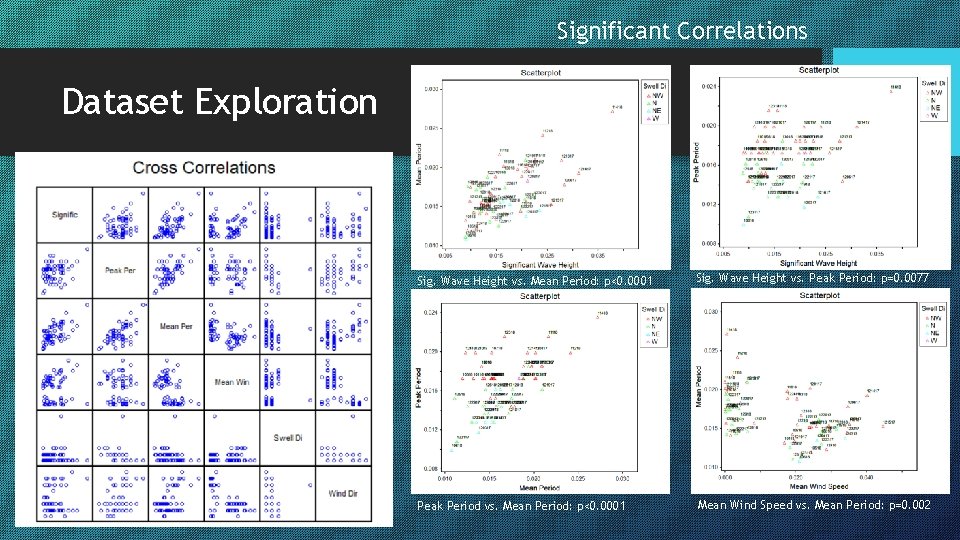
Significant Correlations Dataset Exploration Sig. Wave Height vs. Mean Period: p<0. 0001 Sig. Wave Height vs. Peak Period: p=0. 0077 Peak Period vs. Mean Period: p<0. 0001 Mean Wind Speed vs. Mean Period: p=0. 002

Dataset Analysis Results needed: -% Variance Extracted of 4 axes -Eigenvalues vs. Broken Stick Eigenvalues -Randomization results w/ p-values -Eigenvectors/variable loadings -Ordination plot

Results Interpretation 1 st Stopping Rule (Eigenvalue > Broken-Stick Eigenvalue) 3 axes meet this criterion The first 3 axes are the PCA axes that explain more variability than would be expected by chance. This is because the Eigenvalue for these axes are larger than the Broken-stick Eigenvalue (which is the eigenvalue produced by chance) for only these columns. 2 nd Stopping Rule (Eigenvalue > Mean Randomization) 2 axes meet this criterion 3 rd Stopping Rule (p value <0. 05) 1 axis meets this criterion

Results Interpretation Coefficient of Determination and Orthogonality R-squared values indicate percent of pattern explained in original distance matrix. Orthogonality indicates independence of axes. Results show 100% orthogonality for each pair of axes.

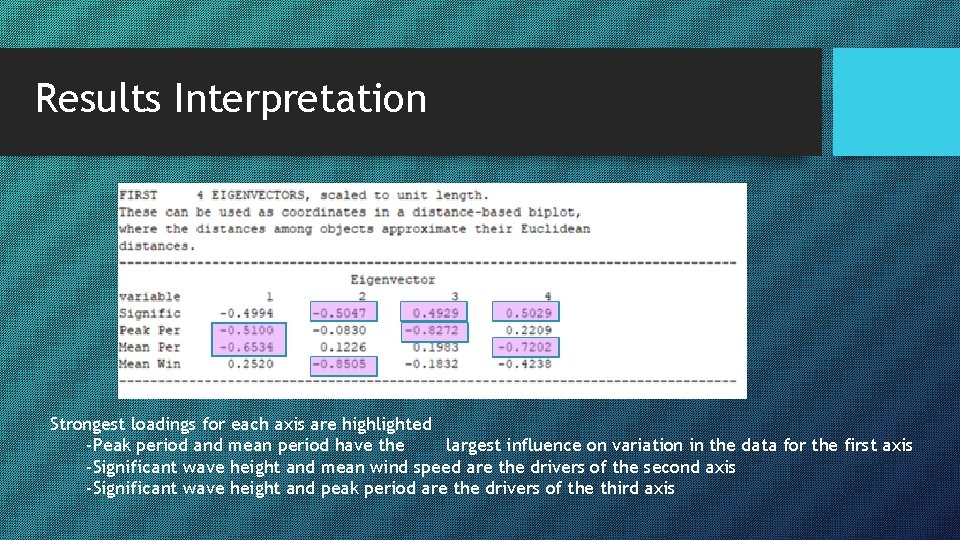
Results Interpretation Strongest loadings for each axis are highlighted -Peak period and mean period have the largest influence on variation in the data for the first axis -Significant wave height and mean wind speed are the drivers of the second axis -Significant wave height and peak period are the drivers of the third axis

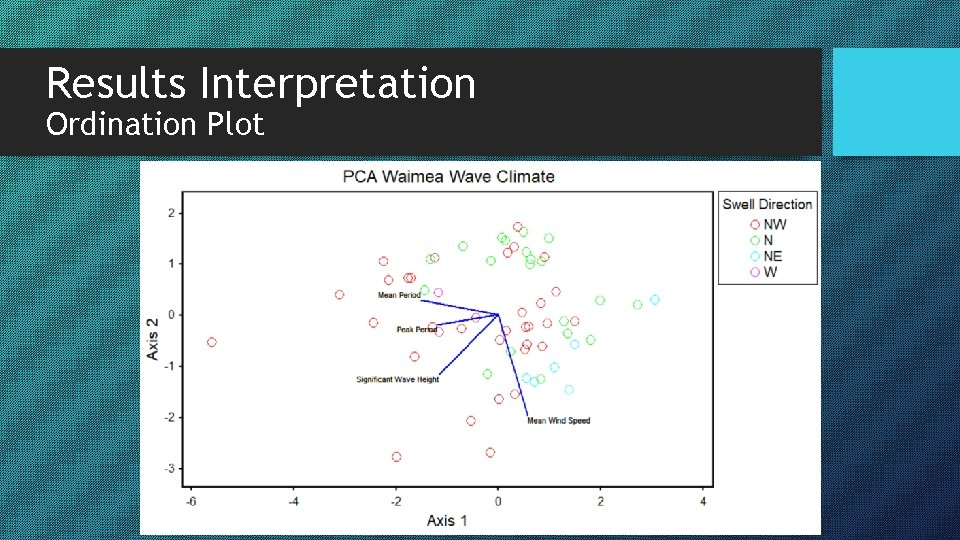
Results Interpretation Ordination Plot

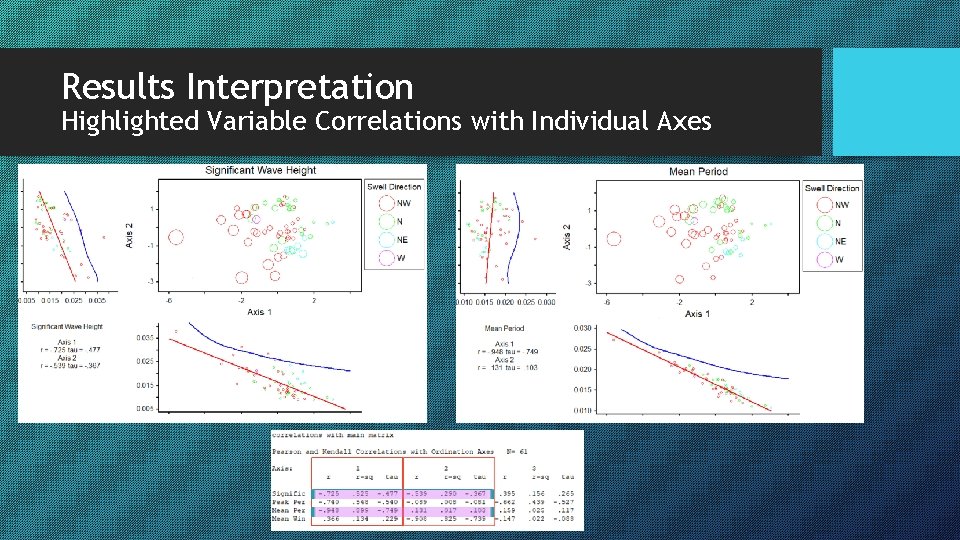
Results Interpretation Highlighted Variable Correlations with Individual Axes

Discussion • The results are fairly consistent with my predictions; significant wave height and mean wave period are significantly correlated with a p-value of <0. 0001 and both have fairly strong loadings for the principal axis. However, when considering all of the variables, the resulting ordination of axes from this PCA indicates that mean period and peak period are the strongest influencers of the variability in the data for the first axis and are therefore the principal components (followed by mean wind speed and significant wave height for the second axis). • This analysis helped me to understand the relationship among variables that relate to wave climate. If historical atmospheric data for this location was easier to obtain, I would like to incorporate more variables such as barometric pressure to attain more interesting insights of wave climate. • For my re-analysis, I would like to perform a polar ordination. The next steps involve selecting endpoints for this analysis.