PATTERNS IN CHAOTICALLY MIXING FLUID FLOWS Arthur Straube

PATTERNS IN CHAOTICALLY MIXING FLUID FLOWS Arthur Straube Department of Physics, University of Potsdam, Germany COLLABORATION: A. Pikovsky, M. Abel URL: http: //www. stat. physik. uni-potsdam. de

OUTLINE · MOTIVATION - mixing in a relation to microfluidics - reaction-advection-diffusion systems: variety of patterns · TEMPORAL CHAOS VS SPATIAL MIXING - nontrivial transition: spacially homogeneous/spacially inhomogeneous state (theory and numerical simulation) · CHEMICAL INSTABILITY INDUCED BY MIXING FLOWS - mixing: leads to homogenezation - can mixing destabilize homogeneous state?
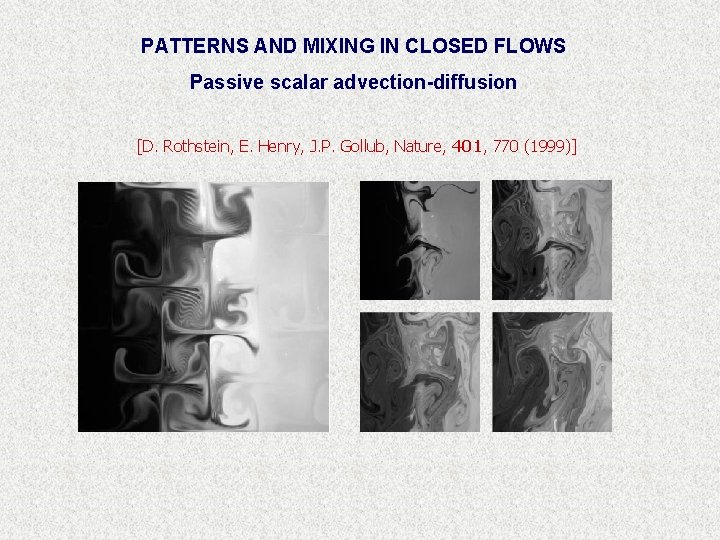
PATTERNS AND MIXING IN CLOSED FLOWS Passive scalar advection-diffusion [D. Rothstein, E. Henry, J. P. Gollub, Nature, 401, 770 (1999)]
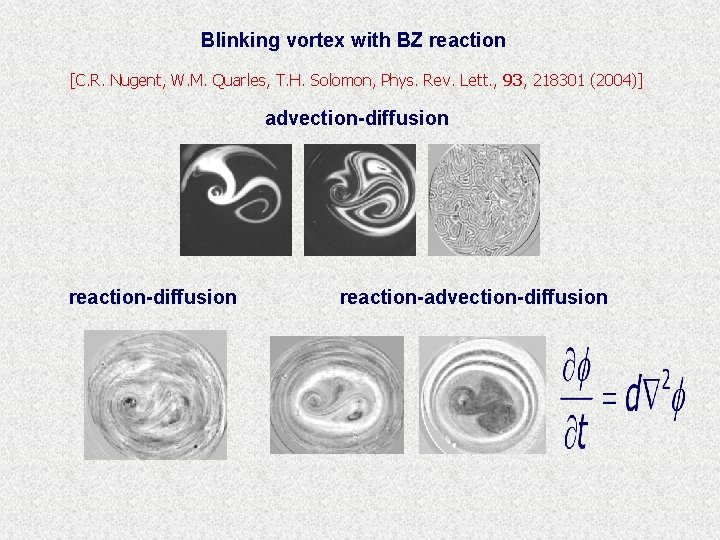
Blinking vortex with BZ reaction [C. R. Nugent, W. M. Quarles, T. H. Solomon, Phys. Rev. Lett. , 93, 218301 (2004)] advection-diffusion reaction-advection-diffusion

TEMPORAL CHAOS VERSUS SPATIAL MIXING [A. Straube, M. Abel, A. Pikovsky, Phys. Rev. Lett. 93, 174501 (2004)] Diffusion of a scalar Advection and diffusion · 2 D time-dependent flow: mixing Reaction · One or two species: fixed point or oscillations. Final state is homogeneous (completely mixed)

To allow for a nontrivial dynamics we consider the dynamics of several species (three or more) We start with the reaction equations: solution Additionally, each component is subjected to advection and diffusion. We also assume · · · the velocity field is incompressible concentrations do not influence the flow no-flux/periodic boundary conditions Reaction-Advection-Diffusion (RAD). Spatio-temporal dynamics
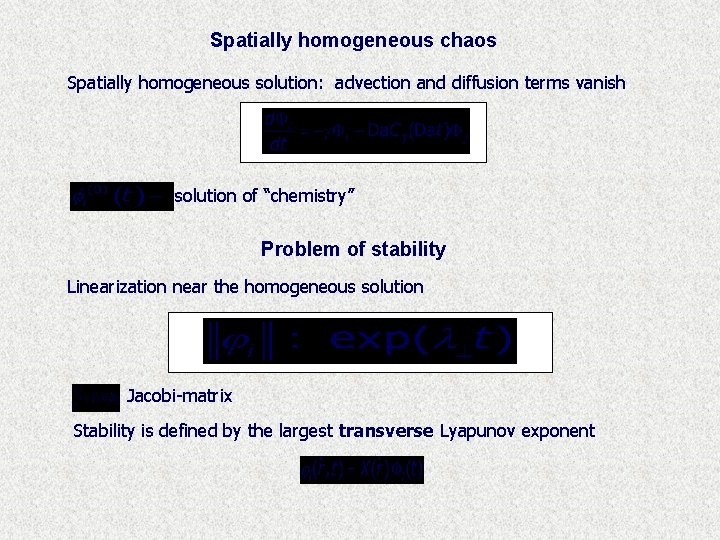
Spatially homogeneous chaos Spatially homogeneous solution: advection and diffusion terms vanish solution of “chemistry” Problem of stability Linearization near the homogeneous solution Jacobi-matrix Stability is defined by the largest transverse Lyapunov exponent

Analytical approach · · time-independent velocity field equal diffusion constants Separation ansatz: Space: eigenvalue problem Smallest nonzero eigenvalue Time: Substitution:

Asymptotic solution: decay of the advection-diffusion mode Lyapunov exponent due to reaction (“chemistry”) Thus: · · · spacially homogeneous regime is stable if a regime with regular (reaction) oscillations is always stable a nontrivial transition is possible only if and large enough The critical reaction rate
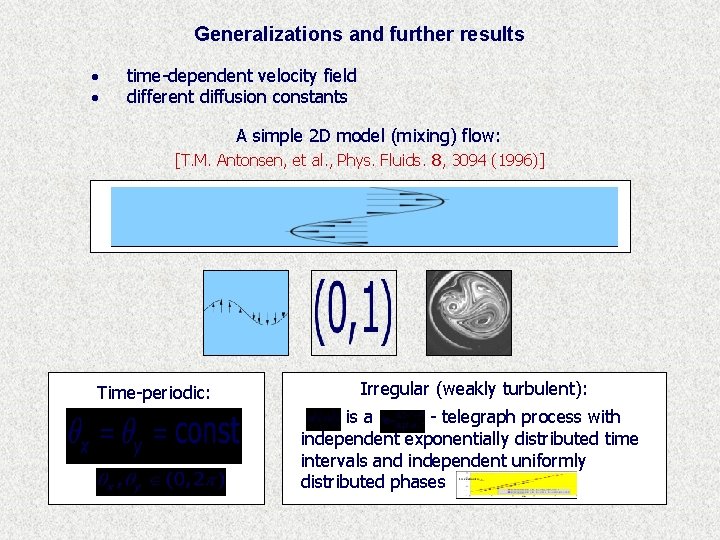
Generalizations and further results · · time-dependent velocity field different diffusion constants A simple 2 D model (mixing) flow: [T. M. Antonsen, et al. , Phys. Fluids. 8, 3094 (1996)] Time-periodic: Irregular (weakly turbulent): is a - telegraph process with independent exponentially distributed time intervals and independent uniformly distributed phases
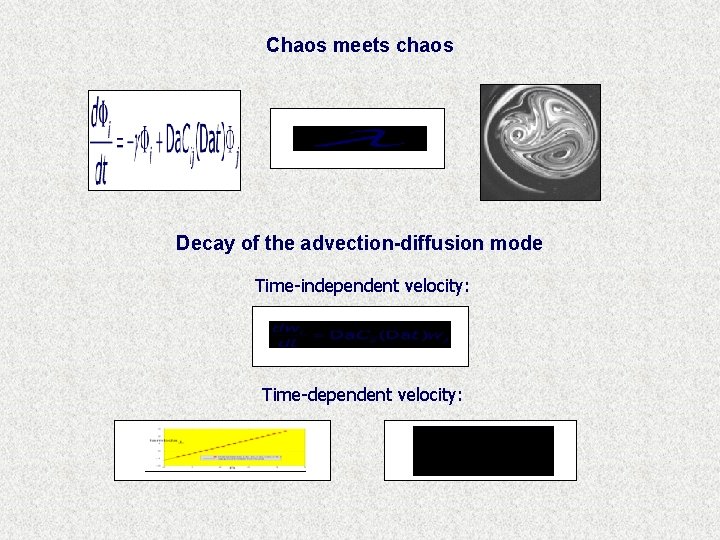
Chaos meets chaos Decay of the advection-diffusion mode Time-independent velocity: Time-dependent velocity:
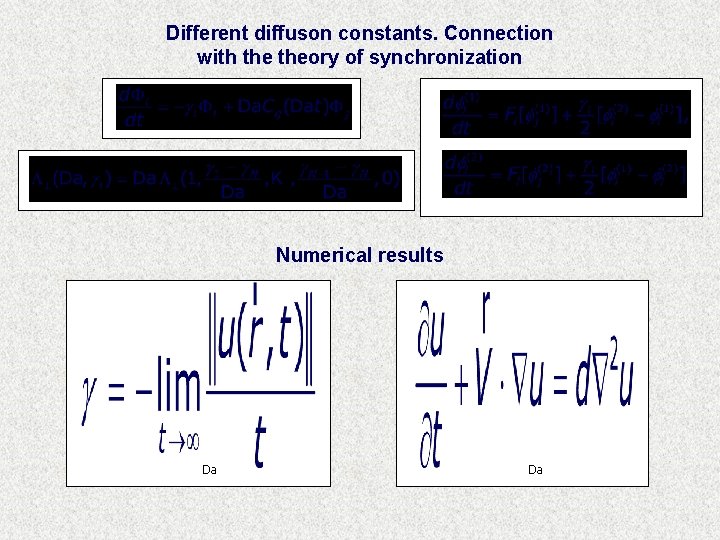
Different diffuson constants. Connection with theory of synchronization Numerical results Da Da
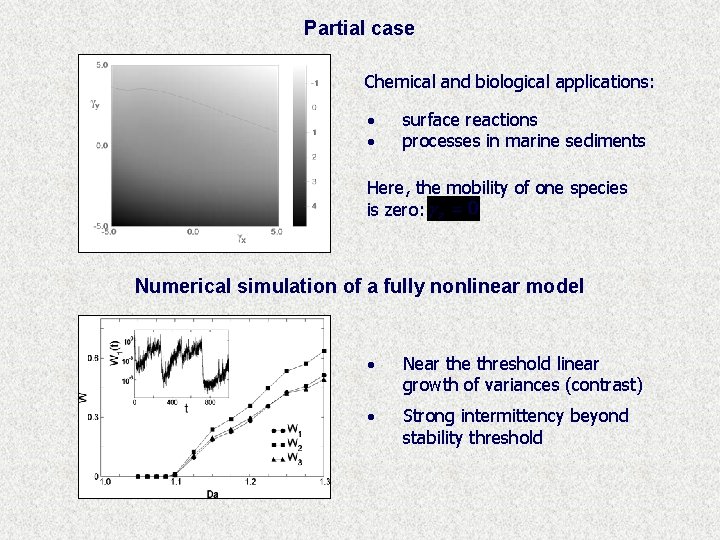
Partial case Chemical and biological applications: · · surface reactions processes in marine sediments Here, the mobility of one species is zero: Numerical simulation of a fully nonlinear model · Near the threshold linear growth of variances (contrast) · Strong intermittency beyond stability threshold
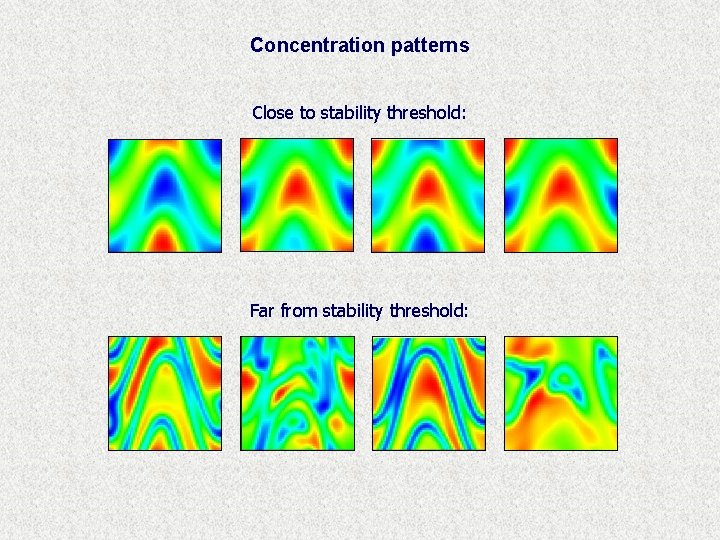
Concentration patterns Close to stability threshold: Far from stability threshold:
![CHEMICAL INSTABILITY INDUCED BY A MIXING FLOW [A. Straube, A. Pikovsky, in progress] RAD CHEMICAL INSTABILITY INDUCED BY A MIXING FLOW [A. Straube, A. Pikovsky, in progress] RAD](http://slidetodoc.com/presentation_image/a815bcf59a560b3738a0ba0ce1ea206b/image-15.jpg)
CHEMICAL INSTABILITY INDUCED BY A MIXING FLOW [A. Straube, A. Pikovsky, in progress] RAD with time-independent reaction Classical Turing instability (no advection)
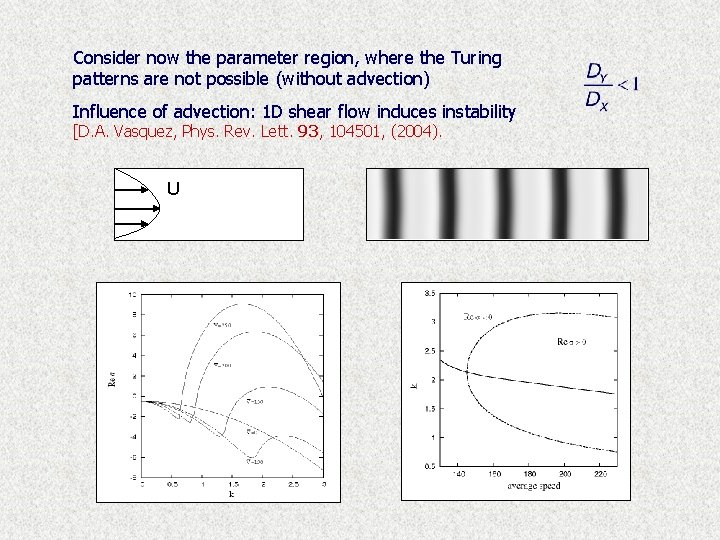
Consider now the parameter region, where the Turing patterns are not possible (without advection) Influence of advection: 1 D shear flow induces instability [D. A. Vasquez, Phys. Rev. Lett. 93, 104501, (2004). U
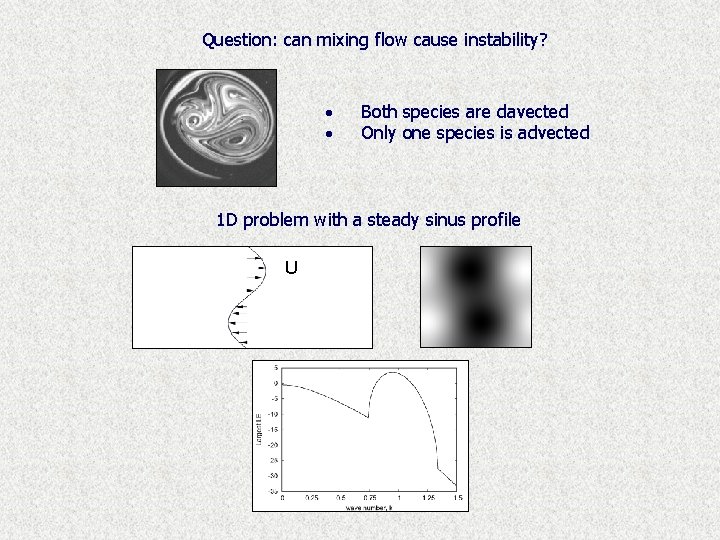
Question: can mixing flow cause instability? · · Both species are davected Only one species is advected 1 D problem with a steady sinus profile U
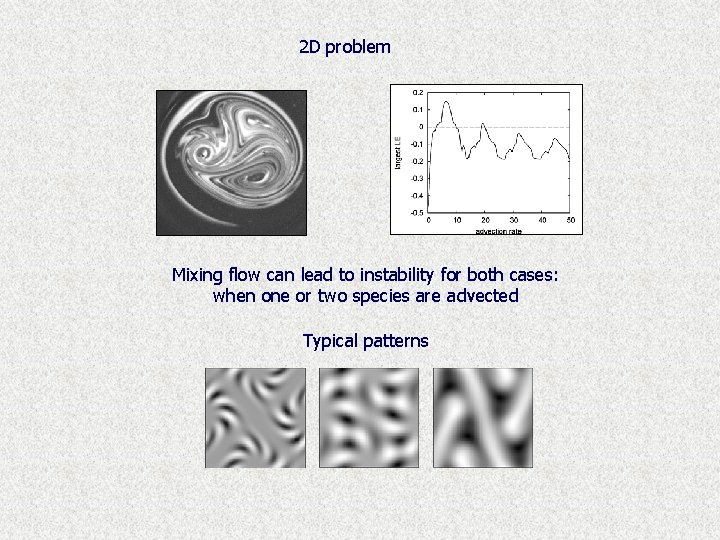
2 D problem Mixing flow can lead to instability for both cases: when one or two species are advected Typical patterns

CONCLUSIONS · Advection-diffusion: decaying, long-living (persistent) patterns · Chaotic reaction leads to nontrivial patterns · Characterization of transition can be done by generalized transversal LE · Mixing flows can induce instability
- Slides: 19