Patterns and Sequences What is a Pattern Things

Patterns and Sequences

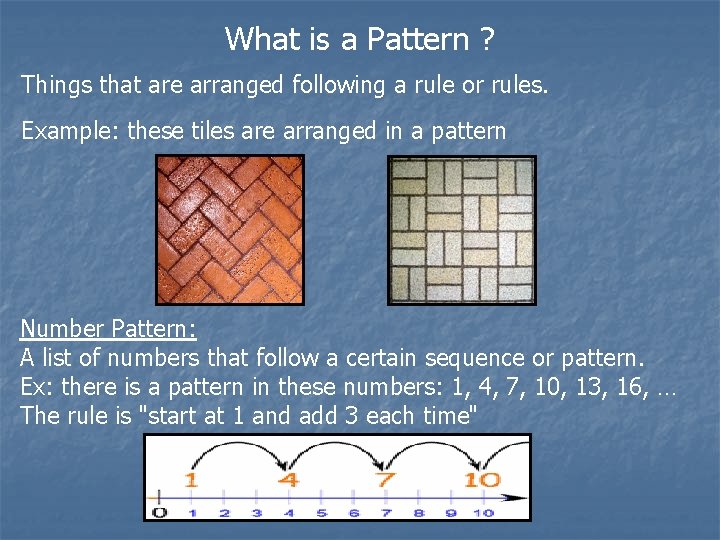
What is a Pattern ? Things that are arranged following a rule or rules. Example: these tiles are arranged in a pattern Number Pattern: A list of numbers that follow a certain sequence or pattern. Ex: there is a pattern in these numbers: 1, 4, 7, 10, 13, 16, … The rule is "start at 1 and add 3 each time"

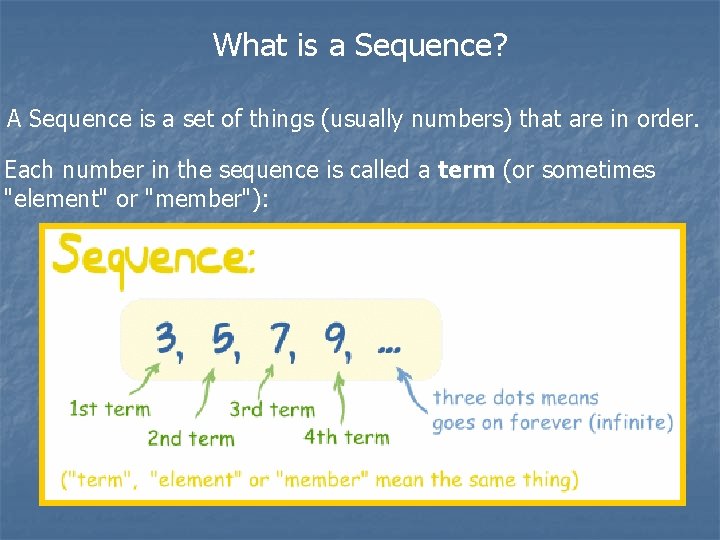
What is a Sequence? A Sequence is a set of things (usually numbers) that are in order. Each number in the sequence is called a term (or sometimes "element" or "member"):

Patterns and sequences For any pattern it is important to try to spot what is happening before you can predict the next number. 1, 2, 3, 4, 5, … What comes next?

Patterns and sequences Look at what is happening from 1 TERM to the next. See if that is what is happening for every TERM. 5, +3 8, +4 3 X 12, +5 17, +6 23, +7 30, …

Finding Missing Numbers To find a missing number or the next number you need to first find a Rule behind the Sequence. Sometimes it is just a matter of looking at the numbers and seeing a pattern Example: 1, 4, 9, 16, ? Answer: they are Squares (12=1, 22=4, 32=9, 42=16, . . . ) Rule: xn = n 2 Sequence: 1, 4, 9, 16, 25, 36, 49, . . . In next slide let us see how to find the 25 th term in this sequence

Example: Finding 25 th Term Remember the rule from last slide: xn = n 2 Did you see how we wrote down that rule with "x" and "n" ? xn means "term number n", so term 3 would be written x 3 And we also used "n" in the formula, so the formula for term 3 is 32 = 9. This could be written x 3 = 32 = 9 Once we have a Rule we can use it to find any term, for example, the 25 th term can be found by "plugging in" 25 wherever n is. x 25 = 252 = 625

http: //www. shodor. org/interactivate/activities/Sierpi nski. Triangle/

Patterns and sequences Now try these patterns: 3, 7, 11, 15, 19, … 128, 64, 32, 16, 8, … 10, 1, … 135, … 1000, 5, 100, 15, 45,