Patternbased Clustering How to cluster the five objects

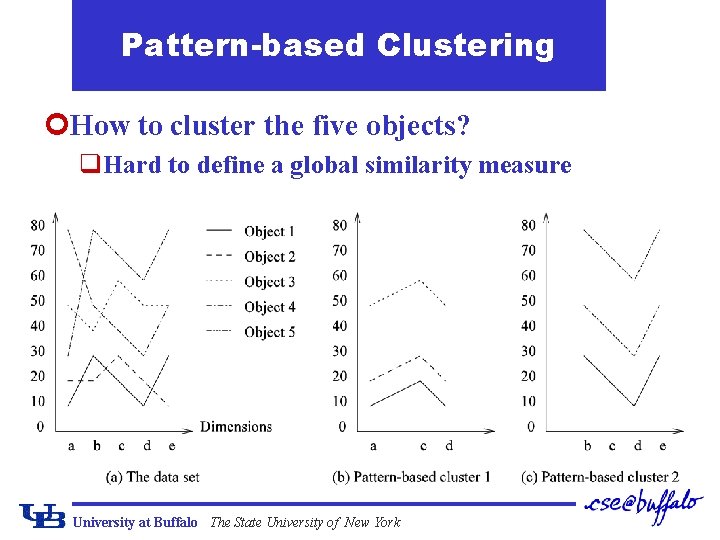
Pattern-based Clustering ¢How to cluster the five objects? q. Hard to define a global similarity measure University at Buffalo The State University of New York

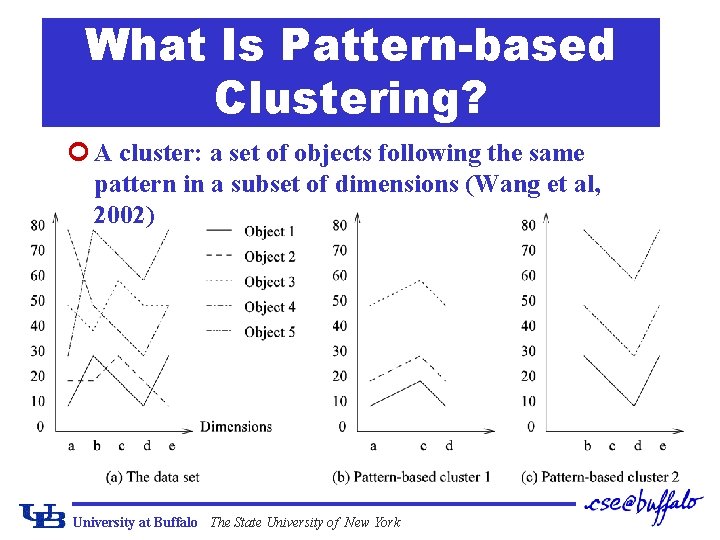
What Is Pattern-based Clustering? ¢ A cluster: a set of objects following the same pattern in a subset of dimensions (Wang et al, 2002) University at Buffalo The State University of New York

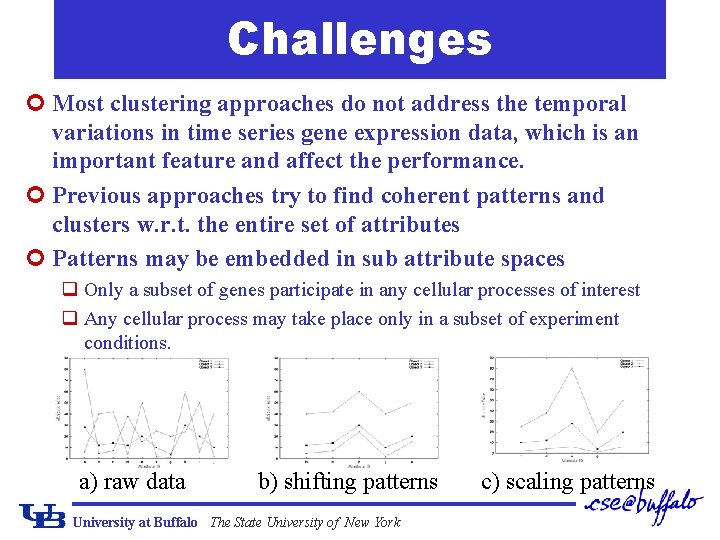
Challenges ¢ Most clustering approaches do not address the temporal variations in time series gene expression data, which is an important feature and affect the performance. ¢ Previous approaches try to find coherent patterns and clusters w. r. t. the entire set of attributes ¢ Patterns may be embedded in sub attribute spaces q Only a subset of genes participate in any cellular processes of interest q Any cellular process may take place only in a subset of experiment conditions. a) raw data b) shifting patterns University at Buffalo The State University of New York c) scaling patterns

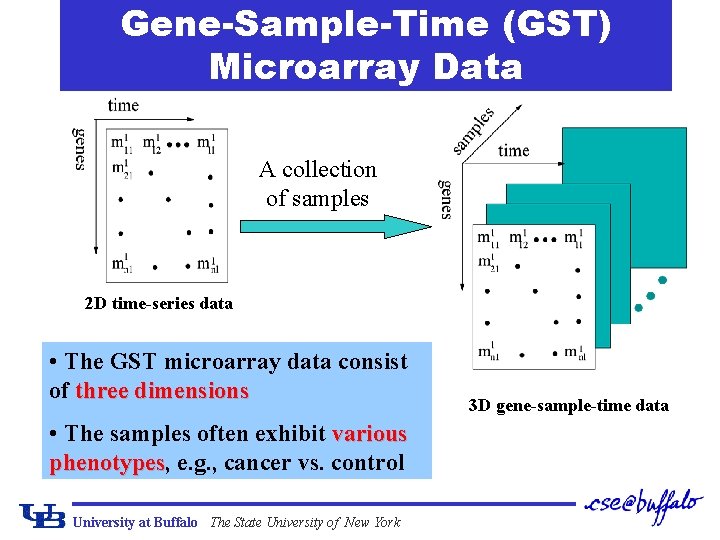
Gene-Sample-Time (GST) Microarray Data A collection of samples 2 D time-series data • The GST microarray data consist of three dimensions • The samples often exhibit various phenotypes, phenotypes e. g. , cancer vs. control University at Buffalo The State University of New York 3 D gene-sample-time data

Challenges of Mining GST Data ¢ Most clustering algorithms were designed for 2 D data, and cannot be directly extended for 3 D data. Challenges 2 D data 3 D data Mining Process Partition genes and samples simultaneously Cluster model Two types of variables Three types of variables University at Buffalo The State University of New York

Coherent Gene Cluster A 3 D GST data set The 2 D representation A coherent gene cluster • The group of samples (sj 1, sj 2, sj 3 ) may exhibit the same phenotype • The group of genes (gi 1, gi 2, gi 3) may be strongly correlated to the phenotype shared by (sj 1, sj 2, sj 3 ) University at Buffalo The State University of New York

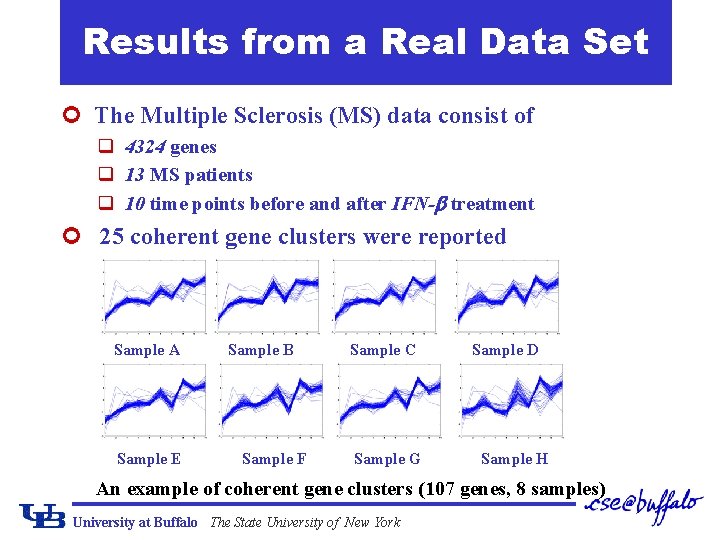
Results from a Real Data Set ¢ The Multiple Sclerosis (MS) data consist of q 4324 genes q 13 MS patients q 10 time points before and after IFN- treatment ¢ 25 coherent gene clusters were reported Sample A Sample E Sample B Sample F Sample C Sample G Sample D Sample H An example of coherent gene clusters (107 genes, 8 samples) University at Buffalo The State University of New York

Other Types of Coherent Clusters University at Buffalo The State University of New York

Problem Definition ¢ Given a GST microarray data matrix M, a maximal coherent gene cluster C=(G S) is a combination of a subset of genes G and a subset of samples S such that: q Coherent : the subset of genes G are coherent across the subset of samples S; q Significant : |G|≥ming, |S|≥mins, where ming and mins are user-specified parameters; q Maximal : any insertion of g G or s S will make C not coherent. ¢ The problem of mining coherent gene clusters is to find the complete set of maximal coherent gene clusters in M. University at Buffalo The State University of New York

Coherence Measure ¢ Various coherence measures exist. ¢ Measure selection is application dependent. ¢ A general coherence model q Given a coherence measure sim( • ) and a user-specified threshold , q A gene ga is coherent on samples si and sj, if sim(pai, paj)≥ . q Coherent gene matrix (G 1, S 1): if every gene gi G 1 is coherent across samples in S 1. q Trivial coherent gene matrix: ({gi}, {sj}), (G, {sj}) ¢ We choose the Person’s correlation coefficient. ¢ Other coherence measures are also applicable. University at Buffalo The State University of New York

Related Work ¢ Clustering algorithms on Gene-Sample or Gene-Time microarray data q The cluster model is completely different ¢ Subspace clustering q Find subsets of objects coherent with subsets of attributes ¢ Frequent pattern mining q Find subsets of items frequently appearing in transaction databases University at Buffalo The State University of New York

Algorithm Outline ¢ Phase 1 (Pre-processing) : For each gene g, find the complete set of maximal coherent sample sets of gene g. ¢ Phase 2: Compute the complete set of maximal coherent gene clusters based on pre -processing results. University at Buffalo The State University of New York

Coherent Sample Sets ¢ Given a gene g, a maximal coherent sample set of g is a subset of samples Si such that: q coherent : g is coherent across Si; q significant : |Si| mins; q maximal : there exists no superset S’ Si such that g is also coherent with S’. ¢ (g Si ) is a building block for coherent gene clusters including g. University at Buffalo The State University of New York

Preprocessing Phase Suppose mins = 3 s 5 s 1 s 2 s 3 s 4 s 5 s 6 s 1 1 1 0 0 s 2 1 1 0 0 s 3 0 0 1 1 s 4 1 0 1 1 s 5 0 0 1 1 s 6 0 0 1 1 The coherence matrix of gene g s 6 s 4 s 1 s 3 s 2 The coherence graph of gene g University at Buffalo The State University of New York s 3 s 4 s 5 s 6 {s 3, s 4, s 5, s 6} is a coherent sample set of gene g

Sample-gene Search ¢ Set enumeration tree q Enumerate all subsets of samples systematically. q Each node on the tree corresponds to a subset of samples. ¢ For each node S q Find the maximal set of genes Gs which is coherent with S University at Buffalo The State University of New York

Set Enumeration Tree {} {a, b} {a, c} {a, d} {b, c} {b, d} {a, b, c} {a, b, d} {a, c, d} {c, d} {b, c, d} {a, b, c, d} The set enumeration tree for {a, b, c, d} University at Buffalo The State University of New York {d}

Find the Maximal Coherent Subset of Genes ¢ After the pre-processing phase: g 1 {s 1, s 2, s 3, s 4, s 5} g 2 {s 1, s 2, s 4}, {s 1, s 5} g 3 {s 1, s 2, s 3, s 4, s 5} g 4 {s 1, s 2, s 3}, {s 5, s 6} g 5 {s 1, s 5, s 6} ¢ Given a subset of samples S, how to find the maximal coherent set of genes GS? q Expensive approach: scan the table once For each S, Gs can be derived by a single scan of the maximal coherent samples of all genes. If S Sj, g Gs. q Efficient approach: use the inverted list. University at Buffalo The State University of New York

The Inverted List Gene Maximal Coherent sample sets g 1 {s 1, s 2, s 3, s 4, s 5} g 2 {s 1, s 2, s 4}, {s 1, s 5} g 3 {s 1, s 2, s 3, s 4, s 5} g 4 {s 1, s 2, s 3}, {s 5, s 6} g 5 {s 1, s 5, s 6} g 2. b 1 g 2. b 2 The table of maximal coherent sample sets for genes Sample The inverted list s 1 {g 1. b 1, g 2. b 2, g 3. b 1, g 4. b 1, g 5. b 1} s 2 {g 1. b 1, g 2. b 1, g 3. b 1, g 4. b 1} s 3 {g 1. b 1, g 3. b 1, g 4. b 1} s 4 {g 1. b 1, g 2. b 1, g 3. b 1} s 5 {g 1. b 1, g 2. b 2, g 3. b 1, g 4. b 2, g 5. b 1} s 6 {g 4. b 2, g 5. b 1} The table of inverted lists for samples University at Buffalo The State University of New York

Intersection Instead of Scanning ¢ Given a subset of samples S={si 1, …, sik}, intersect the inverted lists of si 1, …, sik. q For example, given S={s 1, s 2, s 3}, Ls 1^Ls 2^Ls 3={g 1. b 1, g 3. b 1, g 4. b 1}, so Gs={g 1, g 3, g 4}. q Suppose the parent of S is S’={si 1, …, sik-1}, then LS=LS’ Lsik. University at Buffalo The State University of New York

Anti-monotonic Property ¢ Given a combination (G S), qif G is not coherent on S, q then for any superset S’ S, G cannot be coherent on S’. ¢ For any descendant S’ of S on the tree q let GS be the maximal coherent gene set of S, q let GS’ be the maximal coherent gene sets of S’, q since S’ S, we have GS’ GS. University at Buffalo The State University of New York

Pruning Irrelevant Samples ¢ Given a subset of samples S={si 1, …, sik}, a sample sj tails, if q j > ik q there exists at least ming genes g such that g is coherent with S {sj} ¢ Samples sl tails(irrelevant samples) cannot be used to extend S. University at Buffalo The State University of New York

Pruning Unpromising Nodes ¢ Given a subset of samples S={si 1, …, sik}, q if |S|+|tails|< mins, then prune the subtree of S. q let the maximal coherent subset of genes of S be Gs, m if there exists (G’ S’) such that ¢ (S tails) S’ ¢ Gs G’, m the prune the subtree of S University at Buffalo The State University of New York

Determination of Maximal Coherent Gene Clusters ¢ The depth-first search strategy: q For any superset S’ of S, S’ is m visited before S; m or a child of S. ¢ To determine whether a coherent gene cluster (Gs S) is maximal, q check (Gs S) after visiting all its children, q report (Gs S) if it is not subsumed. University at Buffalo The State University of New York

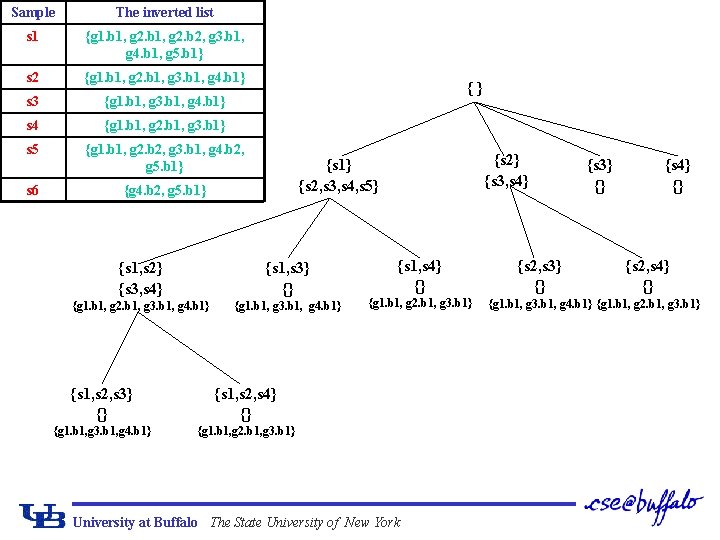
Sample The inverted list s 1 {g 1. b 1, g 2. b 2, g 3. b 1, g 4. b 1, g 5. b 1} s 2 {g 1. b 1, g 2. b 1, g 3. b 1, g 4. b 1} s 3 {g 1. b 1, g 3. b 1, g 4. b 1} s 4 {g 1. b 1, g 2. b 1, g 3. b 1} s 5 {g 1. b 1, g 2. b 2, g 3. b 1, g 4. b 2, g 5. b 1} s 6 {g 4. b 2, g 5. b 1} {} {s 2} {s 3, s 4} {s 1} {s 2, s 3, s 4, s 5} {s 1, s 2} {s 3, s 4} {s 1, s 3} {} {g 1. b 1, g 2. b 1, g 3. b 1, g 4. b 1} {g 1. b 1, g 3. b 1, g 4. b 1} {s 1, s 2, s 3} {} {s 1, s 2, s 4} {} {g 1. b 1, g 3. b 1, g 4. b 1} {g 1. b 1, g 2. b 1, g 3. b 1} {s 1, s 4} {} {g 1. b 1, g 2. b 1, g 3. b 1} University at Buffalo The State University of New York {s 2, s 3} {} {s 4} {} {s 2, s 4} {} {g 1. b 1, g 3. b 1, g 4. b 1} {g 1. b 1, g 2. b 1, g 3. b 1}

Mining Coherent Gene Clusters ¢ Systematic enumeration of genes and samples q Sample-Gene Search q Gene-Sample Search ¢ Pruning rules ¢ Determination of whether a coherent gene cluster (G S) is maximal University at Buffalo The State University of New York

Gene-sample Search Sample-Gene Search Gene-Sample Search Subjects to enumerate samples genes Number of subjects to enumerate 101~102 103~104 Single set of maxmial coherent genes Single or multiple sets of maxmial coherent sample High Low Coherent objects Efficiency on GST data University at Buffalo The State University of New York

Experiment Data Sets ¢ Real-world gene expression data q 4324 genes q 13 multiple sclerosis (MS) patients q before and at 1, 2, 4, 8, 24, 48, 120 and 168 hours after IFN- treatment ¢ Synthetic data q Given the number of genes NG, samples NS and coherent gene clusters NC q Simulate the pre-processing results q Embed NC maximal coherent gene clusters (G S) University at Buffalo The State University of New York

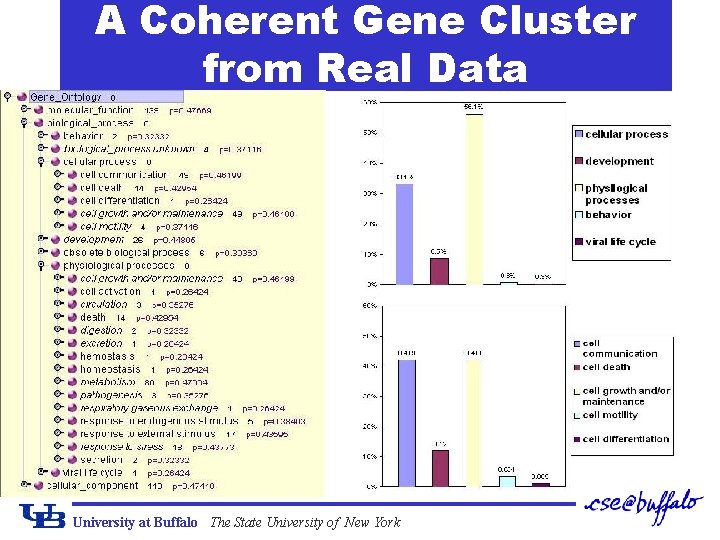
A Coherent Gene Cluster from Real Data University at Buffalo The State University of New York

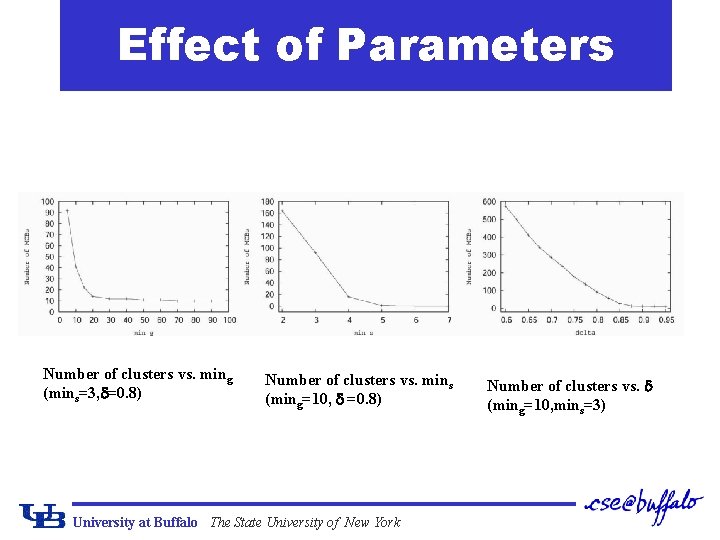
Effect of Parameters Number of clusters vs. ming (mins=3, =0. 8) Number of clusters vs. mins (ming=10, =0. 8) University at Buffalo The State University of New York Number of clusters vs. (ming=10, mins=3)

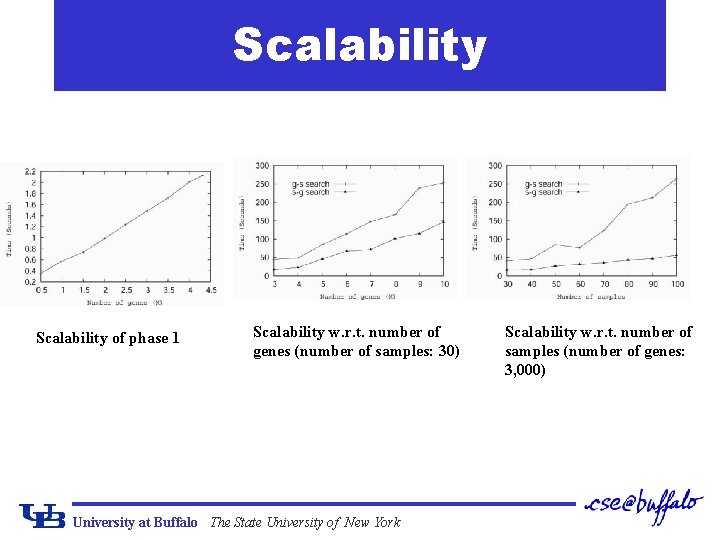
Scalability of phase 1 Scalability w. r. t. number of genes (number of samples: 30) University at Buffalo The State University of New York Scalability w. r. t. number of samples (number of genes: 3, 000)

Conclusion ¢ We define the new problem of mining coherent gene clusters from the novel genesample-time microarray data. ¢ We propose two approaches: the samplegene search and the gene-sample search. ¢ We conduct an extensive empirical evaluation on both real and synthetic data sets. University at Buffalo The State University of New York

Future Work ¢ New problems from the gene-sample-time microarray data: q Coherent sample clusters (G S) m for each s S, any pair of genes gi, gj G has coherent patterns. q Coherent gene-sample clusters (G S), m both a coherent gene cluster and a coherent sample cluster. University at Buffalo The State University of New York