Pattern Recognition Thomas Triplet BAYESIAN STRUCTURE LEARNING March

Pattern Recognition Thomas Triplet BAYESIAN STRUCTURE LEARNING March 2007

2 About structure learning So far, structure of DAG is known Method to learn parameters Learn STRUCTURE of the DAG from the data with an unknown relative frequency distribution Bayesian Structure Learning – Pattern recognition – Thomas Triplet

3 Outline Learning Discrete Variables Model Averaging Learning with Missing Data Probabilistic Model Selection Hidden Variable DAG Models Approximate Model Selection Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables Outline Schema for Learning Structure Procedure for Learning structure Learning from observational / experimental data Complexity of Structure Learning Bayesian Structure Learning – Pattern recognition – Thomas Triplet 4

1. Discrete Variables 1. 1. Schema for learning structure Preliminaries: Recall from § 2. 3. 1 Markov equivalence disjoint equivalence classes All DAG in a given Markov equivalence are faithful to the same distribution Can create a DAG pattern to represent the class Can identify a unique DAG pattern (not a unique DAG) within the conditional independencies Bayesian Structure Learning – Pattern recognition – Thomas Triplet 5

1. Discrete Variables 1. 1. Schema for learning structure Preliminaries: Notations GP : Random variable whose possible values are DAG patterns gp A DAG pattern event is the event that the DAG pattern gp is faithful to the relative frequency distribution We only consider DAG patterns events, not DAG events ρ|�� is a density function Bayesian Structure Learning – Pattern recognition – Thomas Triplet 6

1. Discrete Variables 1. 1. Schema for learning structure Definition Multinomial Bayesian network structure learning schema n random variables X 1, …, Xn with discrete joint probability distribution P, An equivalent sample size N, For each DAG pattern gp containing the n variables, a ), ρ|�� multinomial augmented network (�� , F(�� ) with equivalent sample size N, in wich �� is any member of the equivalence class represented by gp , such that P is the probability distribution in its embedded Bayesian network. Bayesian Structure Learning – Pattern recognition – Thomas Triplet 7

1. Discrete Variables 1. 1. Schema for learning structure Example Multinomial Bayesian network structure learning schema containing 2 variables 2 random variables X 1 and X 2 in {1, 2} P(X 1=1, X 2=1)=0. 25 P(X 1=1, X 2=2)=0. 25 P(X 1=2, X 2=1)=0. 25 P(X 1=2, X 2=2)=0. 25 Bayesian Structure Learning – Pattern recognition – Thomas Triplet 8

1. Discrete Variables 1. 1. Schema for learning structure Example Multinomial Bayesian network structure learning schema containing 2 variables Specify N=4 Bayesian Structure Learning – Pattern recognition – Thomas Triplet 9
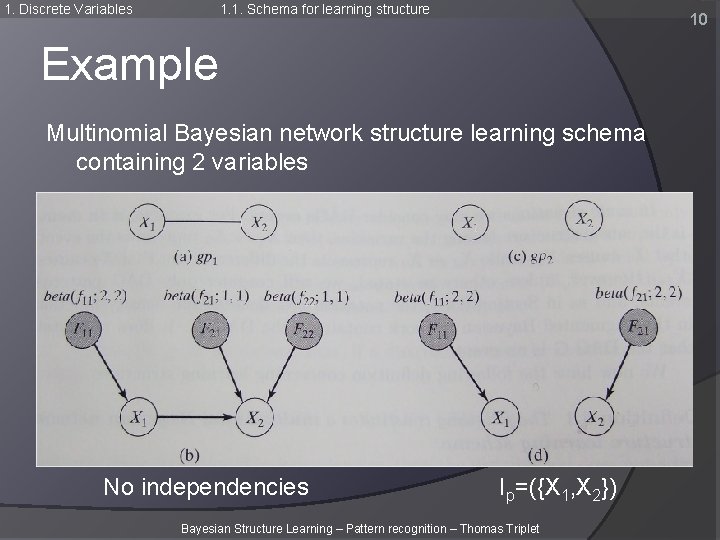
1. Discrete Variables 1. 1. Schema for learning structure 10 Example Multinomial Bayesian network structure learning schema containing 2 variables No independencies Ip=({X 1, X 2}) Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 1. 2. Procedure for learning structure 11 Definition Multinomial Bayesian network structure learning space A multinomial Bayesian network structure learning schema containing the variables X 1, …, Xn A random variable GP whose range consists of all DAG patterns containing the n variables and for each value gp of GP, a prior probability P(gp) A set D = {X(1), …, X(M)} of n-dimensional vectors such that each Xi(h) has the same space as Xi Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 1. 2. Procedure for learning structure 12 Vocabulary Model selection: Determining and selection the DAG patterns with maximum probability conditional on the data Purpose: Learn a DAG pattern along with its parameters for decision making Bayesian Structure Learning – Pattern recognition – Thomas Triplet
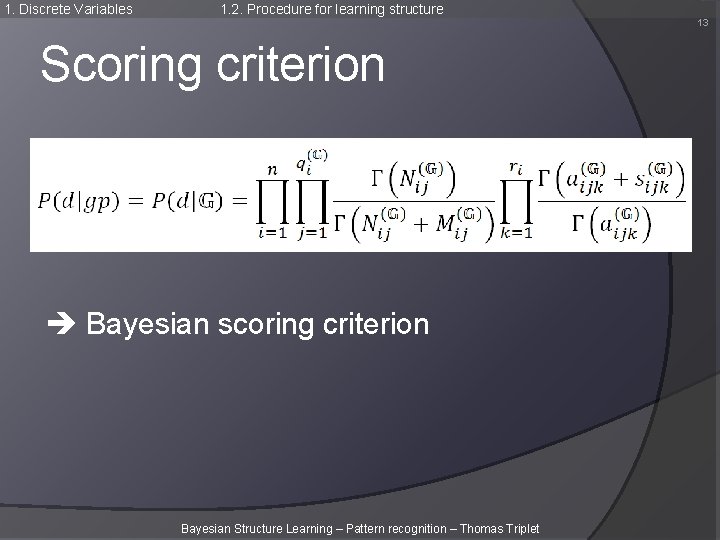
1. Discrete Variables 1. 2. Procedure for learning structure 13 Scoring criterion Bayesian scoring criterion Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 1. 2. Procedure for learning structure 14 Example Variable Value 1 X 1 2 1 X 2 2 Data: Description Individual graduated college Individual did not graduate college Individual was divorced by age of 50 Individual was not divorced by age of 50 Case X 1 X 2 1 1 1 5 1 1 2 6 2 1 3 1 1 7 1 1 4 2 2 8 2 2 Bayesian Structure Learning – Pattern recognition – Thomas Triplet
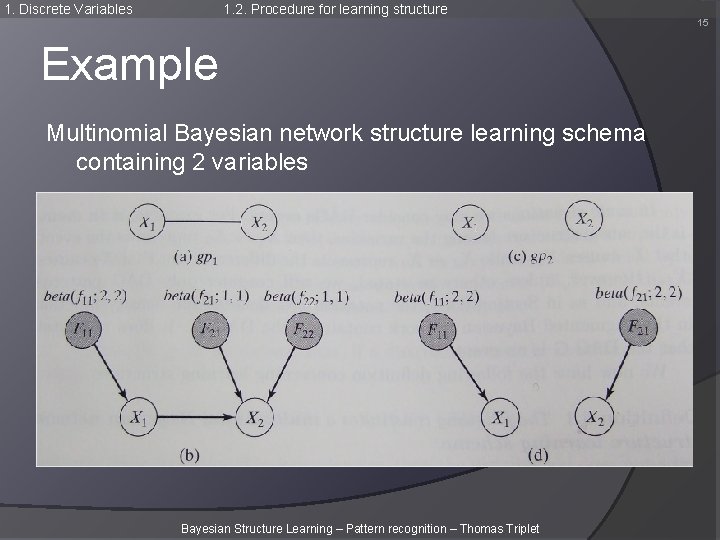
1. Discrete Variables 1. 2. Procedure for learning structure 15 Example Multinomial Bayesian network structure learning schema containing 2 variables Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 1. 4. Complexity of Structure Learning Complexity of Structure learning F(2) = 3 F(3) = 25 F(5) = 29. 000 F(10) = 4. 8 x 1018 Bayesian Structure Learning – Pattern recognition – Thomas Triplet 16

1. Discrete Variables 2. Model averaging 17 2. Model Averaging When? A structure is not overwhelmingly most probable What to do? Averaging over all structures Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 2. Model averaging 18 Model Averaging: procedure 1. Computation of the probability of each DAG pattern 2. Multiplication using the probability of the structure posterior Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 2. Model averaging Example We want to compute: Bayesian Structure Learning – Pattern recognition – Thomas Triplet 19

1. Discrete Variables 3. Missing data 20 3. Missing Data Different approaches Monte-Carlo Methods Gibb’s sampling Large-Sample Approximations Laplace Bayesian Information Criterion (BIC) Cheeseman-Stutz (CS) Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 3. Missing data Comparisons of algorithms Probability computation ○ With MAP values Laplace > CS >> BIC ○ With ML values Laplace > BIC > CS Model selection Laplace ≈ CS ≈ Gibb’s >> BIC Run-time CS ≈ BIC >> Laplace > Gibb’s Bayesian Structure Learning – Pattern recognition – Thomas Triplet 21

1. Discrete Variables 4. Probabilistic Model Selection Outline Probabilistic Models The Model Selection Model Using the Bayesian Scoring Criterion for Model Selection Bayesian Structure Learning – Pattern recognition – Thomas Triplet 22

1. Discrete Variables 4. Probabilistic Model Selection 23 Probabilistic Models: definition Probabilistic model M for a set of random variables V Set of joint probability distributions of the variables Usually specified using a parameter set F and rules to determine the distribution from the parameter set If P M, we say P is included in M Bayesian network model (= DAG model) DAG G=(V, E) as well as a parameter set F Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 4. Probabilistic Model Selection 24 Probabilistic Models: example We toss a die (X) and a coin (Y) X { 1, 2, 3, 4, 5, 6 } and Y { heads, tails } Example of probabilistic model for the joint distribution: F={ f 11, f 12, f 13, f 14, f 15, f 16, f 21, f 22 } with 0 fij 1 ; and P(X=i, Y= heads) = f 1 i * f 21 P(X=i, Y= tails) = f 1 i * f 22 Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 4. Probabilistic Model Selection The model selection problem Find a concise model which, based on a random sample of observations from the population which determines P, includes P Bayesian Structure Learning – Pattern recognition – Thomas Triplet 25

1. Discrete Variables 4. Probabilistic Model Selection Consistent score Definition If M 1 includes P and M 2 does not: If M 1 and M 2 include P and M 1 has a smaller dimension Ex: The Bayesian Scoring Criterion is consistent Bayesian Structure Learning – Pattern recognition – Thomas Triplet 26

1. Discrete Variables 5. Hidden variables DAG models 5. Hidden Variables DAG models Definition G=(V u H, E) Purpose Obtain more models than those obtained considering G=(V, E) Bayesian Structure Learning – Pattern recognition – Thomas Triplet 27
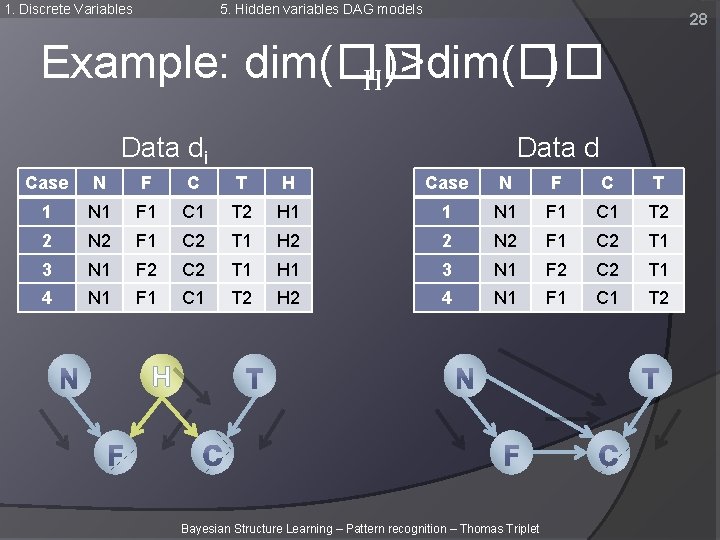
1. Discrete Variables 5. Hidden variables DAG models 28 Example: dim(�� ) H)>dim(�� Data di Data d Case N F C T H Case N F C T 1 N 1 F 1 C 1 T 2 H 1 1 N 1 F 1 C 1 T 2 2 N 2 F 1 C 2 T 1 H 2 2 N 2 F 1 C 2 T 1 3 N 1 F 2 C 2 T 1 H 1 3 N 1 F 2 C 2 T 1 4 N 1 F 1 C 1 T 2 H 2 4 N 1 F 1 C 1 T 2 H Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 5. Hidden variables DAG models Scoring value M: sample size di: ith data on the 5 variables N, F, C, T and H Bayesian Structure Learning – Pattern recognition – Thomas Triplet 29

1. Discrete Variables 5. Hidden variables DAG models Winner? Assuming that: Data set is large enough �� H includes the generative distribution P �� does not include P We have: Bayesian Structure Learning – Pattern recognition – Thomas Triplet 30

1. Discrete Variables 5. Hidden variables DAG models Problem How to choose the hidden variables? More details in chapter 10… Bayesian Structure Learning – Pattern recognition – Thomas Triplet 31

1. Discrete Variables 5. Hidden variables DAG models Models containing the same conditional independencies as DAG models Distribution P can faithfully be embedded in 2 DAGs and yet, but included in only one. Bayesian Structure Learning – Pattern recognition – Thomas Triplet 32
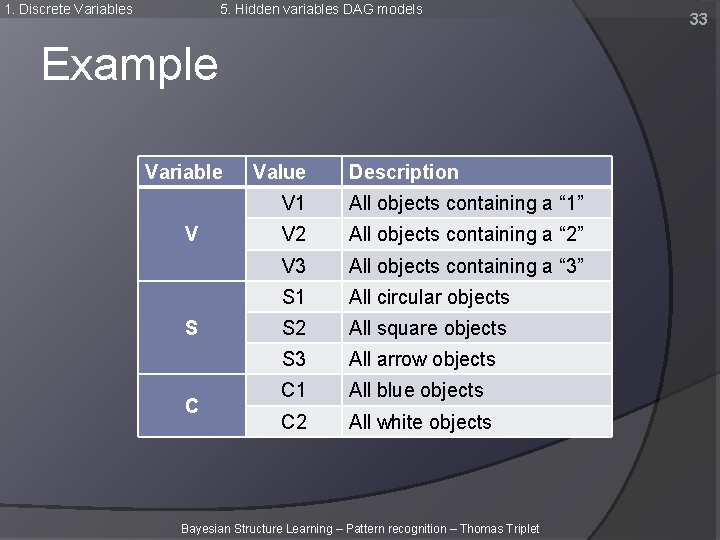
1. Discrete Variables 5. Hidden variables DAG models Example Variable V S C Value Description V 1 All objects containing a “ 1” V 2 All objects containing a “ 2” V 3 All objects containing a “ 3” S 1 All circular objects S 2 All square objects S 3 All arrow objects C 1 All blue objects C 2 All white objects Bayesian Structure Learning – Pattern recognition – Thomas Triplet 33
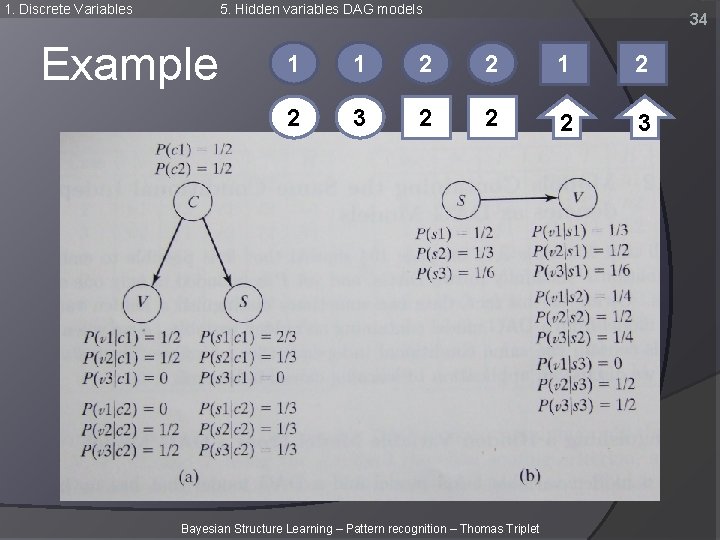
1. Discrete Variables 5. Hidden variables DAG models Example 34 1 1 2 2 3 2 2 2 3 Bayesian Structure Learning – Pattern recognition – Thomas Triplet
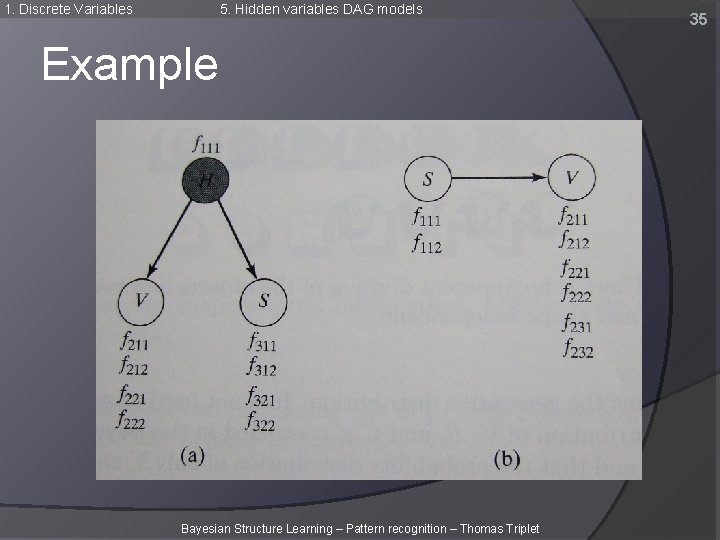
1. Discrete Variables 5. Hidden variables DAG models Example Bayesian Structure Learning – Pattern recognition – Thomas Triplet 35

1. Discrete Variables 5. Hidden variables DAG models Dimension of hidden variable model Number n Dimension of of Hidden Cmp. observable Variable DAG variables model 1 1 < 2 3 < 3 n 7 2 n+1 = 2 n d n>7 > 2 n+1 For binary variables Bayesian Structure Learning – Pattern recognition – Thomas Triplet 36
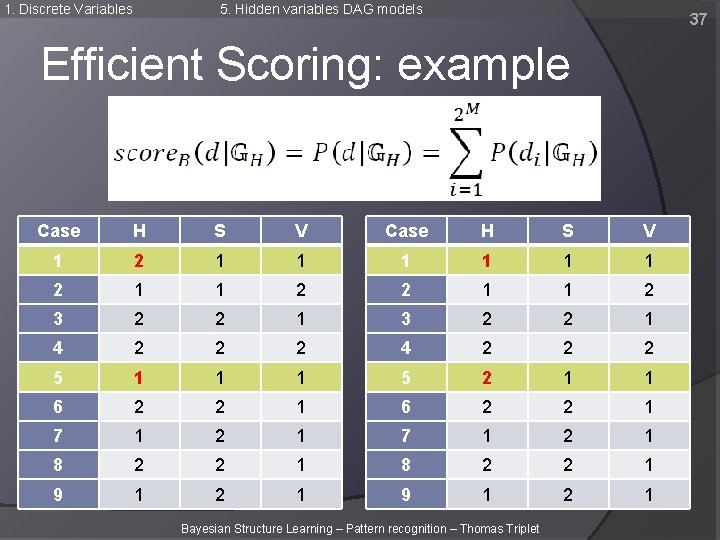
1. Discrete Variables 5. Hidden variables DAG models 37 Efficient Scoring: example Case H S V 1 2 1 1 2 3 2 2 1 4 2 2 2 5 1 1 1 5 2 1 1 6 2 2 1 7 1 2 1 8 2 2 1 9 1 2 1 Bayesian Structure Learning – Pattern recognition – Thomas Triplet

1. Discrete Variables 5. Hidden variables DAG models Efficient Scoring: algorithm Bayesian Structure Learning – Pattern recognition – Thomas Triplet 38

1. Discrete Variables 5. Hidden variables DAG models Efficient Scoring: complexity n r M F number of variables in the network maximum space size number of cases number of different instantiations of the variables Bayesian Structure Learning – Pattern recognition – Thomas Triplet 39

2. Approximate Bayesian Structure Learning Why? When the number of variables is not small, computationally infeasible to consider all DAG patterns to find the best one. Bayesian Structure Learning – Pattern recognition – Thomas Triplet 40

2. Approximate Bayesian Structure Learning 41 Approximate Model Selection Heuristic Solution close to optimum Search space Contains all candidate solution. Ex: All DAGs containing the n variables Bayesian Structure Learning – Pattern recognition – Thomas Triplet

2. Approximate Bayesian Structure Learning 1. The K 2 Algorithm The K 2 algorithm Initialization: PAi = Ø and score. B(d, Xi, PA) For each node Xi (ordered) Find Xi, max in Pred(Xi) that most increases score. B(d, Xi, PA) Add Xi, max to PAi Repeat while a node can increase score. B Complexity: O(n 4. M. r) Bayesian Structure Learning – Pattern recognition – Thomas Triplet 42
2. Approximate Bayesian Structure Learning 1. The K 2 Algorithm Example: ALARM network Bayesian Structure Learning – Pattern recognition – Thomas Triplet 43

44 Thank you ? Bayesian Structure Learning – Pattern recognition – Thomas Triplet

Pattern Recognition Thomas Triplet BAYESIAN STRUCTURE LEARNING March 2007
- Slides: 45