Pattern Recognition Concepts n n Chapter 4 Shapiro

Pattern Recognition Concepts n n Chapter 4: Shapiro and Stockman How should objects be represented? Algorithms for recognition/matching * nearest neighbors * decision tree * decision functions * artificial neural networks How should learning/training be done? Stockman CSE 803 Fall 2008 1

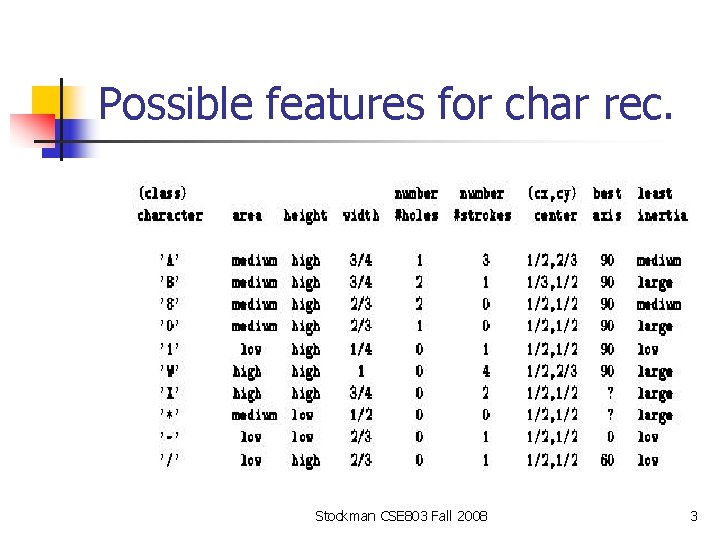
Feature Vector Representation n n X=[x 1, x 2, … , xn], each xj a real number Xj may be object measurement Xj may be count of object parts Example: object rep. [#holes, A, moments, ] Stockman CSE 803 Fall 2008 2

Possible features for char rec. Stockman CSE 803 Fall 2008 3

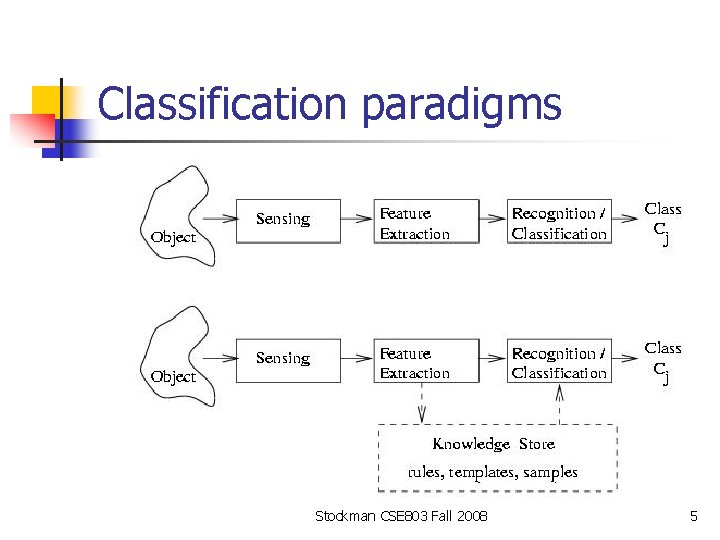
Some Terminology n n n Classes: set of m known classes of objects (a) might have known description for each (b) might have set of samples for each Reject Class: a generic class for objects not in any of the designated known classes Classifier: Assigns object to a class based on features Stockman CSE 803 Fall 2008 4

Classification paradigms Stockman CSE 803 Fall 2008 5

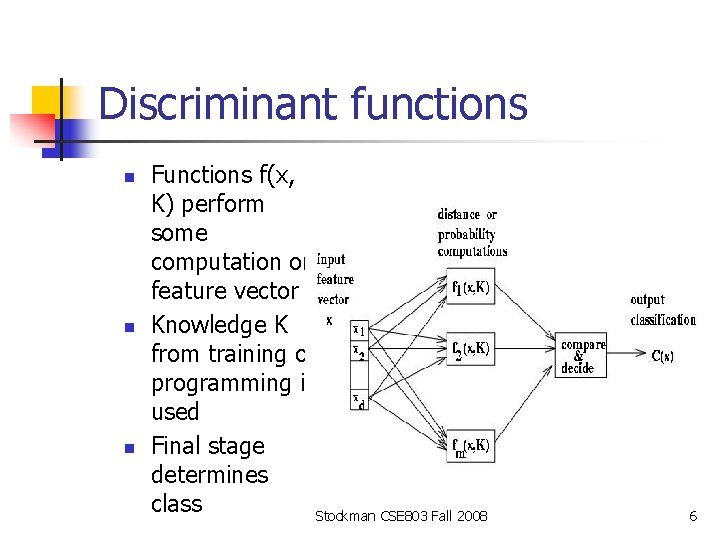
Discriminant functions n n n Functions f(x, K) perform some computation on feature vector x Knowledge K from training or programming is used Final stage determines class Stockman CSE 803 Fall 2008 6

Decision-Tree Classifier n n n Uses subsets of features in seq. Feature extraction may be interleaved with classification decisions Can be easy to design and efficient in execution Stockman CSE 803 Fall 2008 7

Classification using nearest class mean n Compute the Euclidean distance between feature vector X and the mean of each class. Choose closest class, if close enough (reject otherwise) Low error rate at left Stockman CSE 803 Fall 2008 8

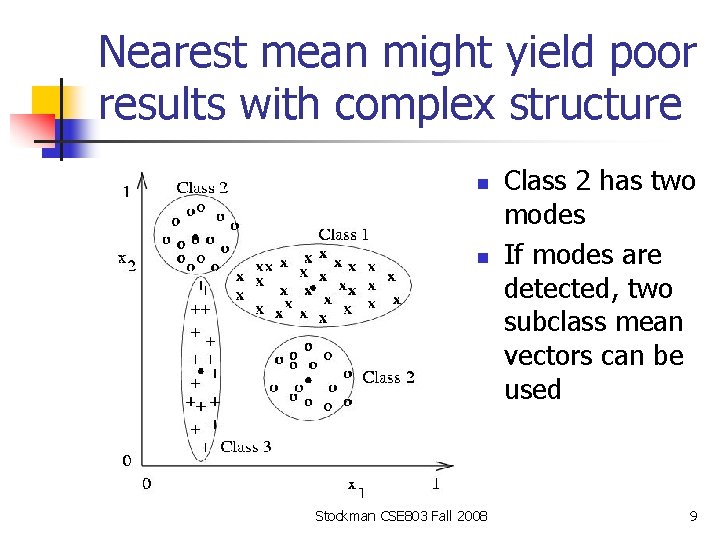
Nearest mean might yield poor results with complex structure n n Stockman CSE 803 Fall 2008 Class 2 has two modes If modes are detected, two subclass mean vectors can be used 9

Scaling coordinates by std dev Stockman CSE 803 Fall 2008 10

Another problem for nearest mean classification n n If unscaled, object X is equidistant from each class mean With scaling X closer to left distribution Coordinate axes not natural for this data 1 D discrimination possible with PCA Stockman CSE 803 Fall 2008 11

Receiver Operating Curve ROC n n Plots correct detection rate versus false alarm rate Generally, false alarms go up with attempts to detect higher percentages of known objects Stockman CSE 803 Fall 2008 12

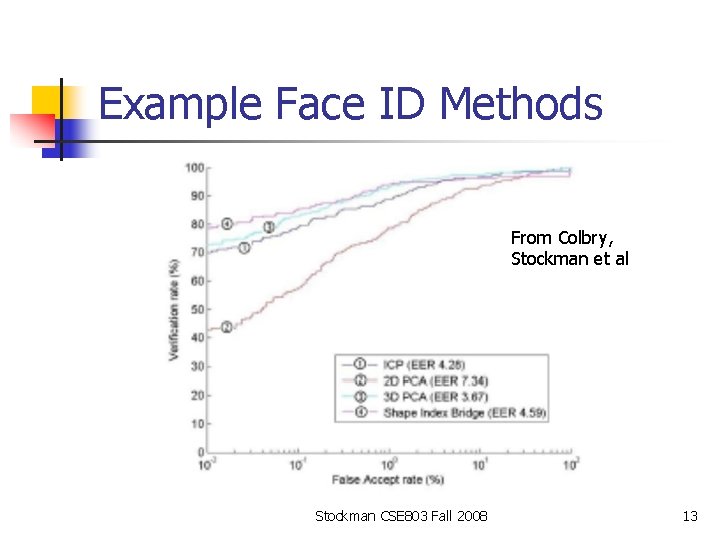
Example Face ID Methods From Colbry, Stockman et al Stockman CSE 803 Fall 2008 13

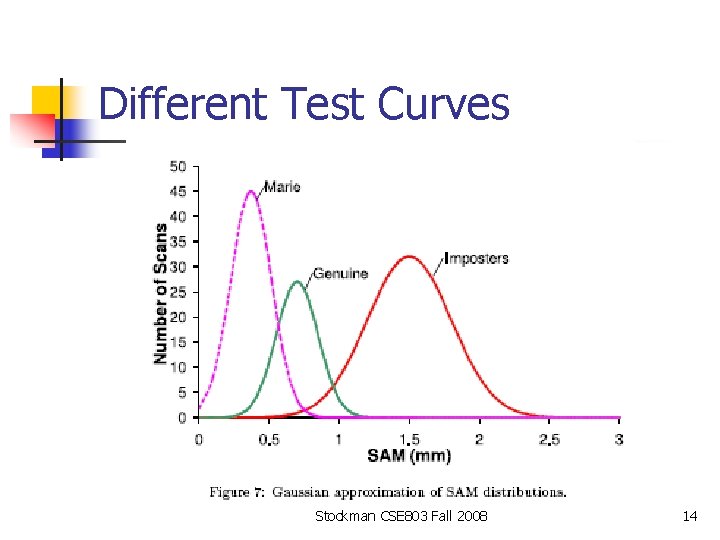
Different Test Curves Stockman CSE 803 Fall 2008 14

Confusion matrix shows empirical performance Stockman CSE 803 Fall 2008 15

Bayesian decision-making Stockman CSE 803 Fall 2008 16

Normal distribution n 0 mean and unit std deviation Table enables us to fit histograms and represent them simply New observation of variable x can then be translated into probability Stockman CSE 803 Fall 2008 17

Parametric Models can be used Stockman CSE 803 Fall 2008 18

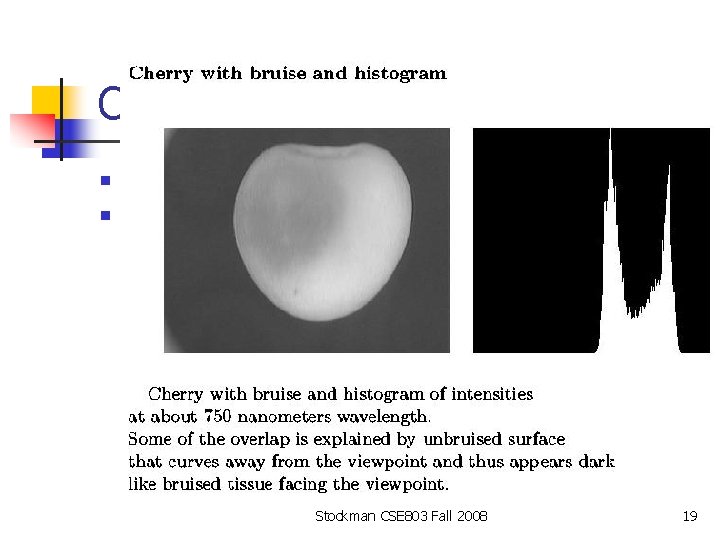
Cherry with bruise n n Intensities at about 750 nanometers wavelength Some overlap caused by cherry surface turning away Stockman CSE 803 Fall 2008 19