Pattern Recognition and Machine Learning Kernel Methods Overview

Pattern Recognition and Machine Learning: Kernel Methods

Overview ¢ Many linear parametric models can be recast into an equivalent dual representation in which the predictions are based on linear combinations of a kernel function evaluated at the training data points ¢ Kernel k(x, x’) = Ф(x)T Ф(x’) l l Ф(x) is a fixed nonlinear feature space mapping Kernel is symmetric of its arguments i. e. k(x, x’) = k(x’, x)

Overview ¢ ¢ Kernel trick or kernel substitution is the general idea that, if we have an algorithm formulated in such a way that the input vector x enters only in the form of scalar products, then we can replace the scalar product with some other choice of kernel Stationary kernels – invariant to translations in input space l ¢ k(x, x’) = k(x-x’) Homogeneous kernels (RBF) – depend only on the magnitude of the distance l k(x, x’) = k(||x-x’||)

Dual Representations

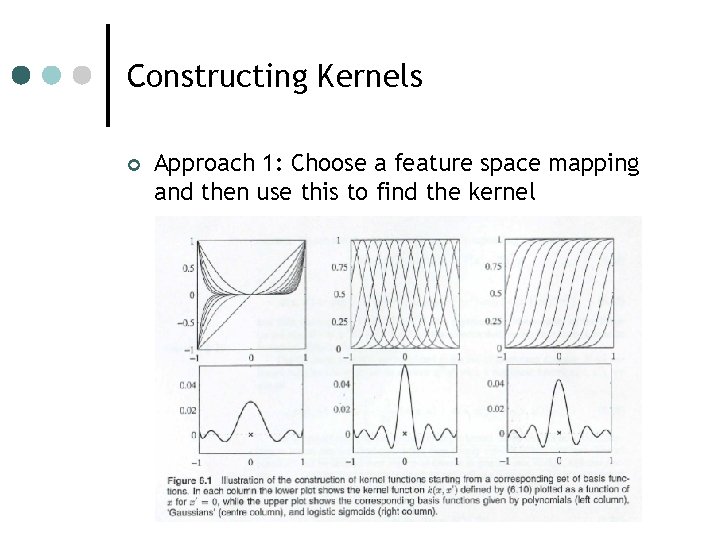
Constructing Kernels ¢ Approach 1: Choose a feature space mapping and then use this to find the kernel

Constructing Kernels ¢ Approach 2: Construct kernel functions directly such that it corresponds to a scalar product in some feature space

Constructing Kernels ¢ A simpler way to test without having to construct Ф(x): l Use the necessary and sufficient condition that for a function k(x, x’) to be a valid kernel, the Gram matrix K, whose elements are given by k(xn, xm), should be positive semidefinite for all possible choices of the set {xn}

Constructing Kernels ¢ Another powerful technique is to build them out of simpler kernels

Radial Basis Functions ¢ Historically introduced for the purpose of exact function interpolation ¢ The values of the coefficients are found by least squares Since there as many constraints as coefficients, results in a function that fits every target value exactly ¢

Radial Basis Functions ¢ Imagine the noise on the input variable x, described by a variable ξ having a distribution (ξ), the sum of squares error function is ¢ Basis function centred on every data point Nadaraya-Watson model ¢

Nadaraya-Watson model ¢ Imagine the noise on the input variable x, described by a variable ξ having a distribution (ξ), the sum of squares error function is ¢ Basis function centred on every data point Nadaraya-Watson model ¢

Nadaraya-Watson model ¢ Imagine the noise on the input variable x, described by a variable ξ having a distribution (ξ), the sum of squares error function is ¢ Basis function centred on every data point Nadaraya-Watson model ¢

Nadaraya-Watson model ¢ Can also be derived from kernel density estimation l ¢ where f(x, t) is the component density function and there is one such component centred on each data point We now find an expression for the regression function y(x), corresponding to the conditional average of the target variable conditioned on the input variable

Nadaraya-Watson model

Nadaraya-Watson model ¢ This model is also known as kernel regression ¢ For a localized kernel function, it has the property of giving more weight to data points that a close to x