PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 1 INTRODUCTION

PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 1: INTRODUCTION

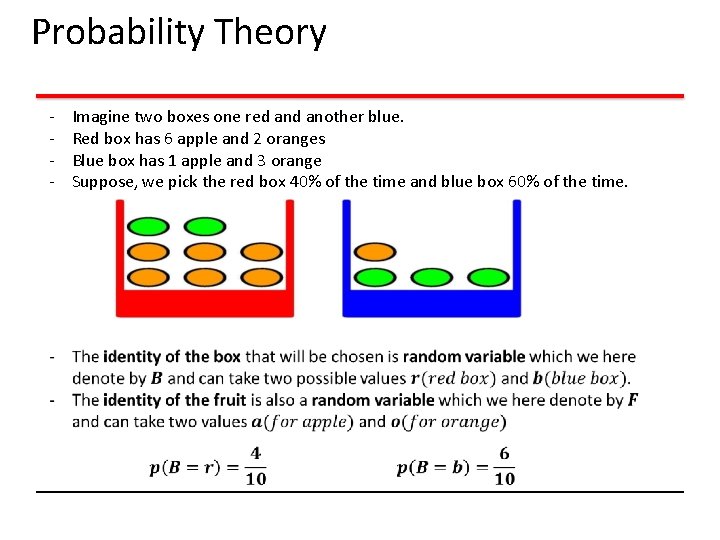
Probability Theory - Imagine two boxes one red another blue. Red box has 6 apple and 2 oranges Blue box has 1 apple and 3 orange Suppose, we pick the red box 40% of the time and blue box 60% of the time.

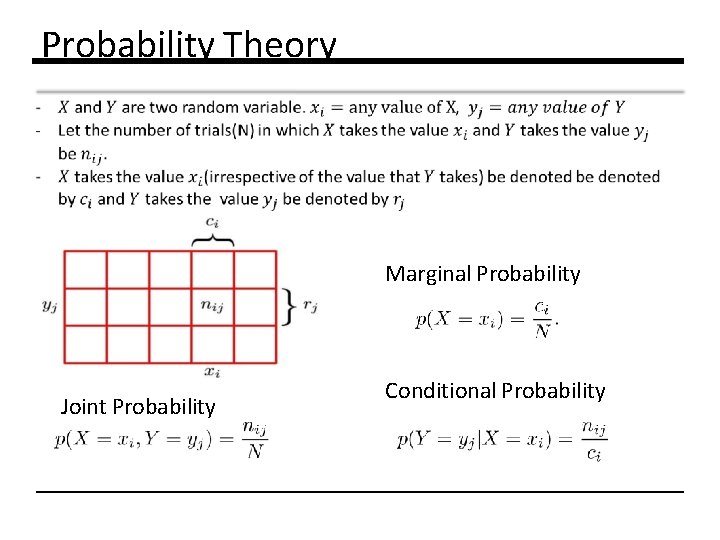
Probability Theory Marginal Probability Joint Probability Conditional Probability

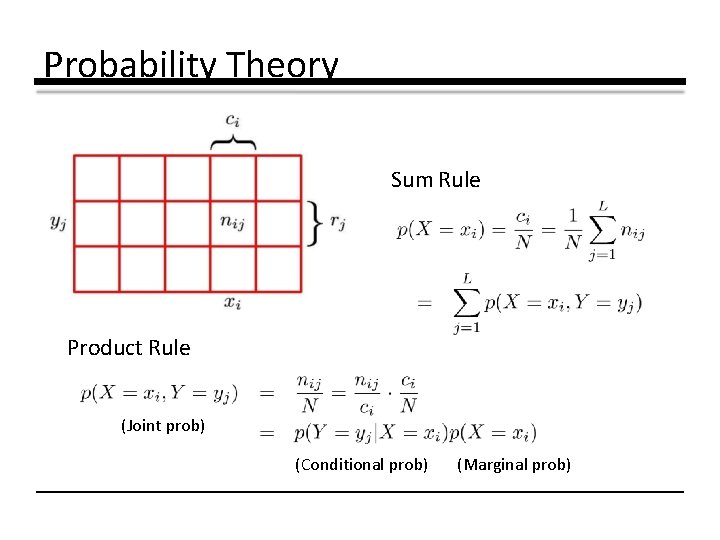
Probability Theory Sum Rule Product Rule (Joint prob) (Conditional prob) (Marginal prob)

The Rules of Probability Sum Rule Product Rule Sum rule = marginal probability Product rule = joint probability

Bayes’ Theorem From the sum rule, denominator in Bayes’ theorem can be expressed in terms of the quantities appearing in numerator. posterior likelihood × prior

Example: from box and fruit Note that these probabilities are normalized so that Similarly, Now using sum and product rules of probability, overall probability of choosing an apple is And ,

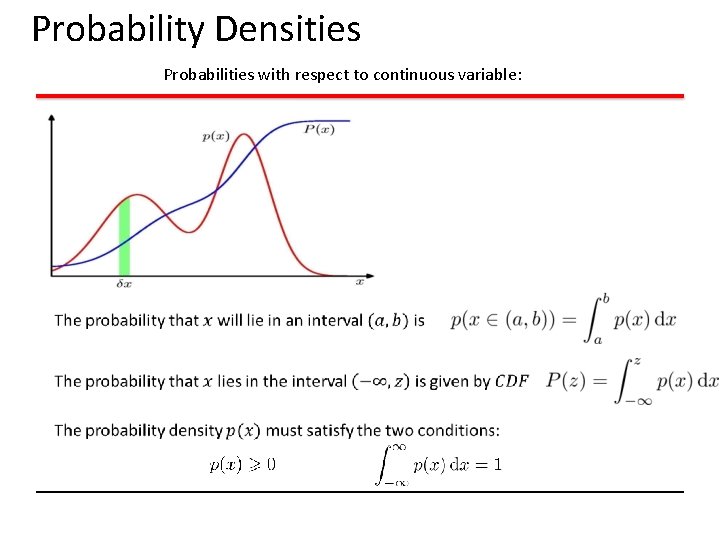
Probability Densities Probabilities with respect to continuous variable:

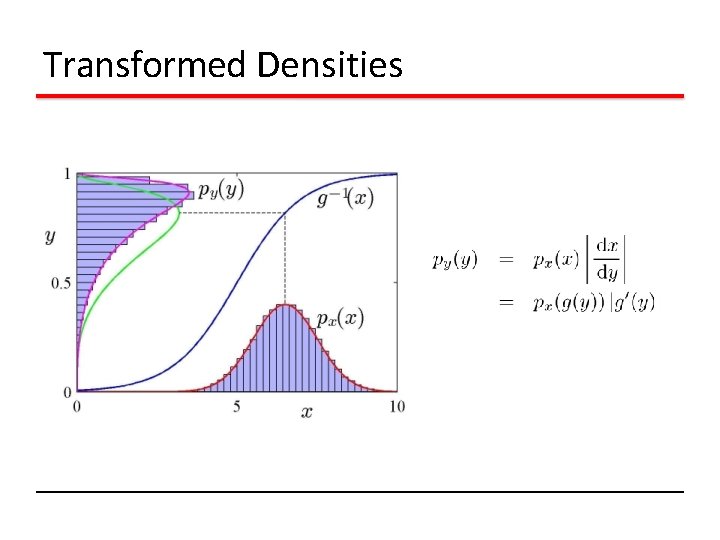
Transformed Densities

Expectations Conditional Expectation (discrete) Approximate Expectation (discrete and continuous)

Variances and Covariances

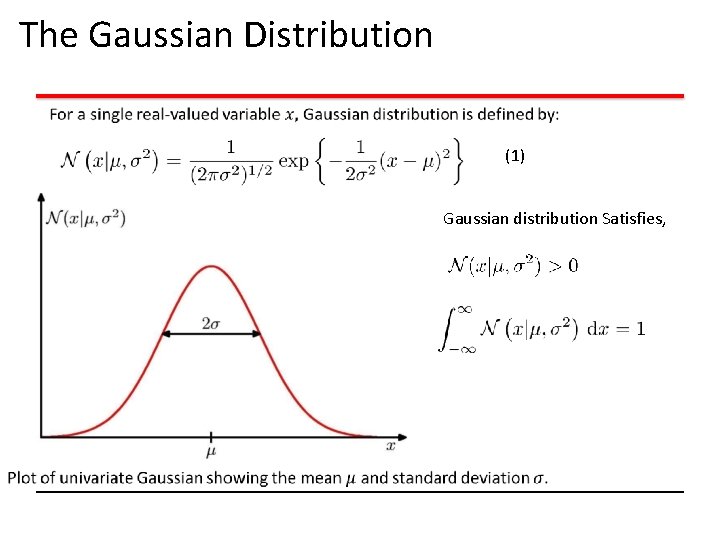
The Gaussian Distribution (1) Gaussian distribution Satisfies,

Gaussian Mean and Variance (2) Similarly for the second order moment: (3) (4)

The Multivariate Gaussian (5) Where,

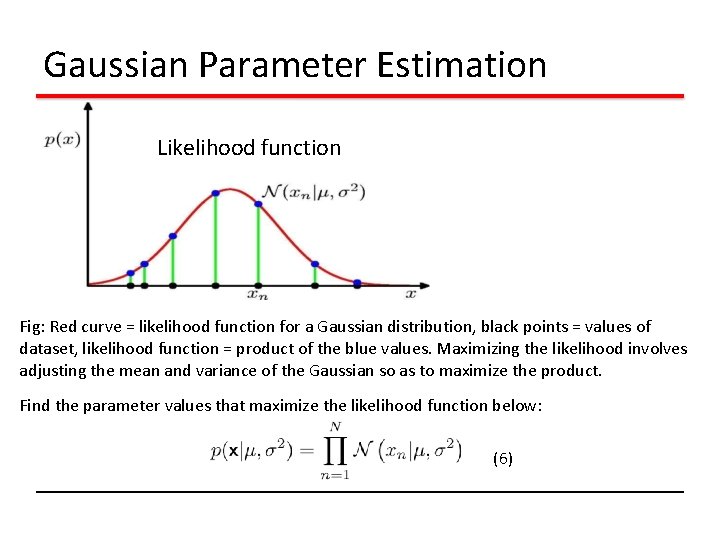
Gaussian Parameter Estimation Likelihood function Fig: Red curve = likelihood function for a Gaussian distribution, black points = values of dataset, likelihood function = product of the blue values. Maximizing the likelihood involves adjusting the mean and variance of the Gaussian so as to maximize the product. Find the parameter values that maximize the likelihood function below: (6)

Maximum (Log) Likelihood Method: Find the parameter values that maximize the likelihood function Maximization of the log of a function is equivalent to maximization of the function itself. From (1) and (6) the log likelihood function can be written as: (7) Maximizing (7) with respect to mean

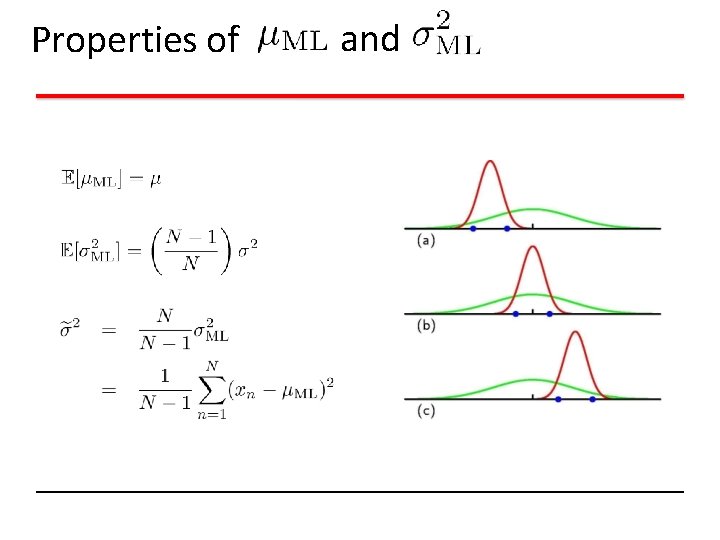
Properties of and

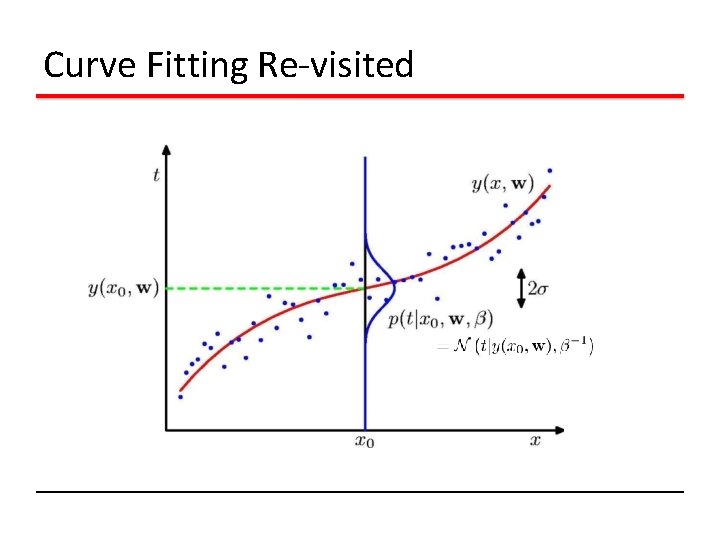
Curve Fitting Re-visited

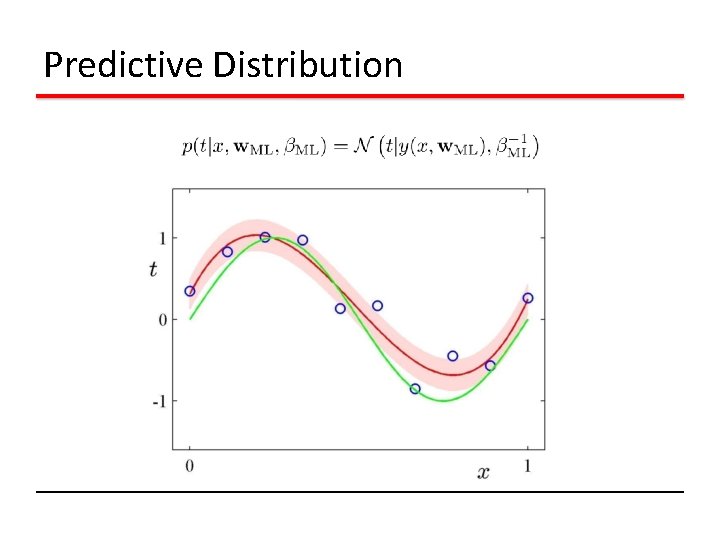
Maximum Likelihood Determine by minimizing sum-of-squares error, .

Predictive Distribution

MAP: A Step towards Bayes Determine by minimizing regularized sum-of-squares error, .

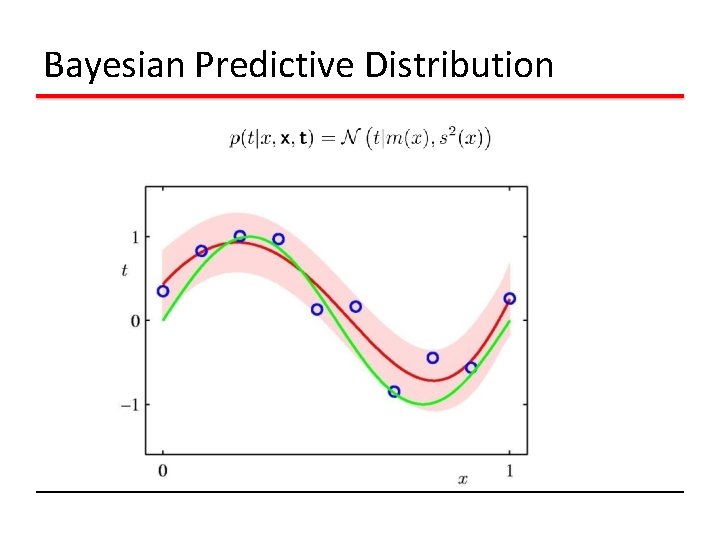
Bayesian Curve Fitting

Bayesian Predictive Distribution

Decision Theory Inference step Determine either or . Decision step For given x, determine optimal t.

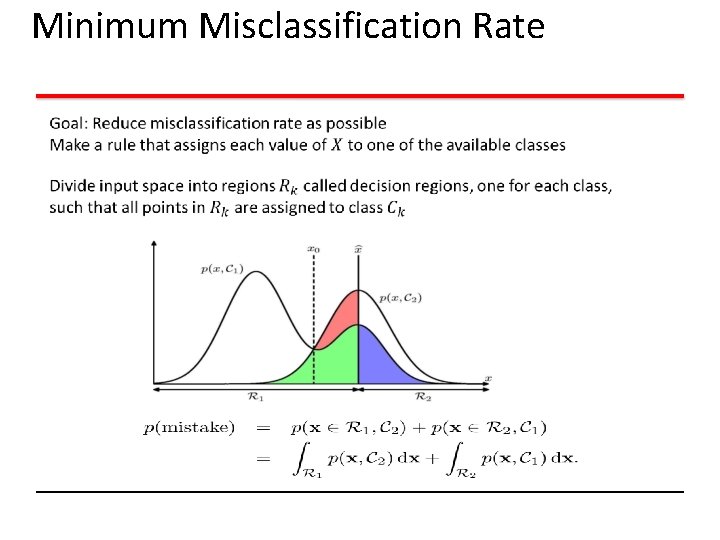
Minimum Misclassification Rate

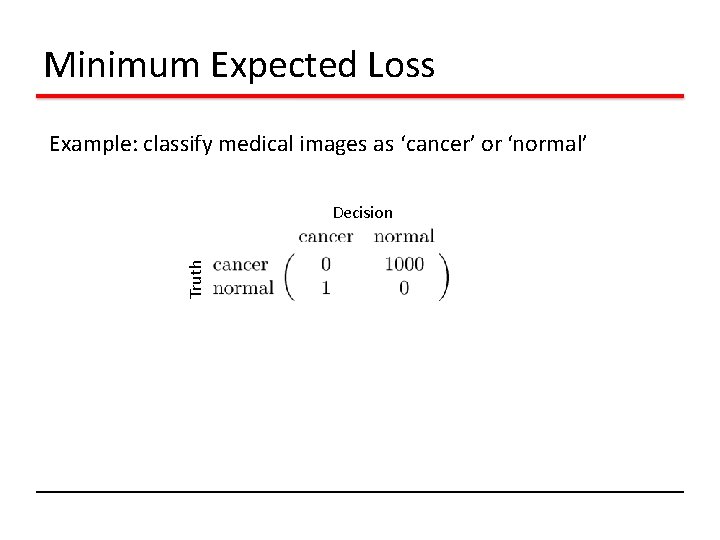
Minimum Expected Loss Example: classify medical images as ‘cancer’ or ‘normal’ Truth Decision

Minimum Expected Loss Goal: minimize the cost or loss function Regions are chosen to minimize

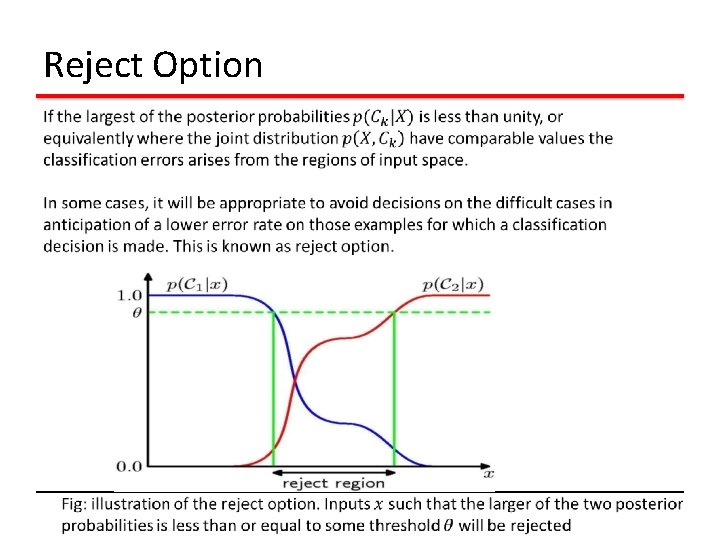
Reject Option

Why Separate Inference and Decision? • • Minimizing risk (loss matrix may change over time) Reject option Unbalanced class priors Combining models

Decision Theory for Regression Inference step Determine . Decision step For given x, make optimal prediction, y(x), for t. Loss function for regression:

The Squared Loss Function

Generative vs Discriminative Generative approach: Model Use Bayes’ theorem Discriminative approach: Model directly

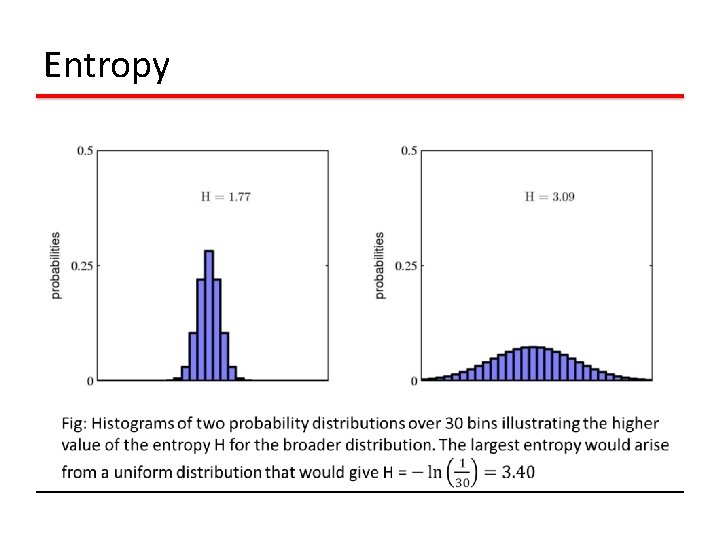
Entropy Important quantity in • coding theory • statistical physics • machine learning

Entropy

Entropy The non uniform distribution has a smaller entropy than the uniform one

Entropy Which is called the multiplicity. The entropy is then defined as the log of the multiplicity scaled by an appropriate constant

Entropy

Differential Entropy Put bins of width ¢ along the real line The quantity on the right-hand side is called the differential entropy. Differential entropy maximized (for fixed ) when So the distribution that maximizes the differential entropy is the Gaussian. If we evaluate the differential entropy of the Gaussian, we obtain

Conditional Entropy Using the product rule, the conditional entropy satisfies the relation:

The Kullback-Leibler Divergence It is not symmetrical quantity. So,

Mutual Information