Pattern Matching Using ngrams With Algebraic Signatures Witold

Pattern Matching Using n-grams With Algebraic Signatures Witold Litwin[1], Riad Mokadem 1, Philippe Rigaux 1 & Thomas Schwarz[2] [1] Université Paris Dauphine [2] Santa Clara University 1

n-gram Search • New pattern matching idea • Matches algebraic signatures • Preprocesses both : pattern & string (record) – String preprocessing is a new idea • To the best of our knowledge • Provides incidental protection of stored data • Important for P 2 P & grid systems • Also called protection against “honest but curious” insider • Fast processing • Especially useful for DBs & longer patterns – ASCII, Unicode, DNA… – Should be then often faster than Boyer-Moore – Possibly the fastest known in this context 2

Algebraic Signature • Symbols of the alphabet are elements of a Galois Field – GF (256) usually • We choose there one primitive element – Usually = 2 • The algebraic signature of the string of i symbols p 1… pi is the sum: p’i = p 1 +…+pi i. • Here the addition and the multiplication are the operations in GF. 3

Algebraic Signature • In our GF (2 f) where f = 8, 16: p + q = p – q = p XOR q • One method for multiplying is : p*q = antilog (( log p + log q) mod 255) • The division is then : p / q = antilog (( log p - log q) mod 255) • The log and antilog are encoded in log and antilog tables with 2 f elements each. – Entry 0 is for element 0 of the GF and is by convention set to 2 f - 1. 4

Cumulative Algebraic Signature • We encode every symbol pi in a string into the signature of the prefix p 1…pi • The value of a CAS symbol now encodes also the knowledge of values of all the previous ones • Matching a single symbol means prefix matching 5

Application of CASs • Protection against involuntary data disclosure • On P 2 P & Grid Servers especially • Numerous CAS encoded string matching algorithms – Prefix match with O (1) complexity – Pattern match by signature only • Karp – Rabin like, linear O (L) complexity – Longest common string search – Longest common prefix search –… 6

CAS Properties • O (K) encoding and decoding speed • For encoding, for instance: p’i = p’i-1 + pi i = CAS ( pi-1) + pi i • Fast n – gram signature calculus – For Sk, l = pk…pl with k > 1 and l – k = n : AS ( Sk, l ) = AS (S l - k+1) = (p’l XOR p’k - 1) / k-1 • Logarithmic Algebraic Signature (LAS) LAS ( Sk, l ) = log AS ( Sk, l ) = = ( log (p’l XOR p’k - 1) – (k-1)) mod 2 f – 1 7

The n-gram Search Key ideas • Design a sublinear pattern match search – With speed about L / K • Apply to CAS encoded DB – New idea for string search algorithm with preprocessing – Justified for a DB • Store once, search many times 8

The n-gram Search Key ideas • Preprocess the pattern to create a jump table – As in Boyer – Moore • Use n –grams with n > 1 to increase the discriminative power of an attempt – Comparison of a sample from the pattern • a single symbol for BM • an LAS of an n – gram for a CAS-encoded string 9

The n-gram Search Key ideas • If the alphabet uses m symbols, the probability that a symbol matches is 1/m – Assuming all symbols equally likely • For usual ASCII pattern matching m = 20 -25 • For DNA m = 4 • A single symbol may often match without the whole pattern matching • e. g. , ¼ times for DNA on the average • Leading to small jumps, – by m symbols on the average 10

The n-gram Search Key ideas • The probability of an n - gram matching may be : min ( 1/ 2 f , 1 / mn ) • In our examples it can reach 1 / 256 – More discriminative sampling – Longer jumps • By almost K or 256 symbols in general • Useful for longer strings – DNA, text, images… 11

ASCII Exemple Usual Alphabet 2 -grams => 5 jumps 1 -gram => 6 jumps 12

DNA Exemple 4 -letter Alphabet 3 jumps 4 jumps 11 jumps 13

The n-gram Search Preprocessing • Encode every record (string) into its CAS – Done for incidental protection anyhow for SDDS-2006 • Encode the terminal n - gram of the searched pattern SK into its LAS in variable V • Fill up the jump table T for every other n - gram in SK – calculate every LAS – for each LAS, store in T its rightmost offset with respect to the end of SK 14

The n-gram Search Jump Table • For GF (256), every n – gram Si, i+n-1 in the pattern and i = LAS (Si, i+n-1): – T ( i ) = the offset – T ( i ) = K – n + 1 otherwise • Remainder : LAS (0) = 255 • T can be also hash table – See the paper – Slower to use but possibly more memory efficient • Probably more useful for a larger GF 15

ASCII Exemple Dauphine V = ne’’ Notation : xy’’ = LAS (xy) 0 7 1 7 … … in’’ 1 … … au’’ 5 … … ph’’ 3 … … 255 7 16

The n-gram Search Processing • Calculate LAS of the current n-gram in the string – Start with the n-gram SK-n+1, K – Continue depending on jump calculus • Attempt to match V – If. true then calculate LAS of the entire current possibly matching substring • of length K and ending with the current n-gram • If. true, then resolve the possible collision – Either attempt to match all the K symbols – Or match enough of terminal n-grams or symbols to decrease the probability of collision to a very small value 17

The n-gram Search Processing • Otherwise – Go to T using LAS of the n-gram – Jump by the number of symbols found in T • Update the “current” position for n-gram to attempt the match – Re-attempt the match as above • Unless the n-gram to attempt is beyond the end of the string 18

ASCII Exemple Again 2 -grams => 5 jumps 1 -gram => 6 jumps 19

DNA Exemple Again 3 jumps 4 jumps 11 jumps 20

n-grams / BM • Average shifts with n-grams can be typically longer • Calculate an attempt & jump may be more expensive as well – About twice as long at first approach – The precise analysis remains to be done • Rule of thumb: If shifts are more than 2 times longer, n-grams with n > 1 or should be faster than BM. 21

Experimental Results • Searching large data of: – DNA – Typical ASCII – XML Documents • Patterns of 6 to 500 symbols (bytes) • 1. 8 GHZ P 3 and 2. 4 GHZ Dual. Core AMD Turion 64 Processors 22

Results Compared to BM • DNA • Up to 72 times faster • Typical ASCII • Up to about 11 times faster • XML Documents • Up to more than 5 times faster • Search faster for longer pattern – Average shifts are longer 23

DNA 24

ASCII 25

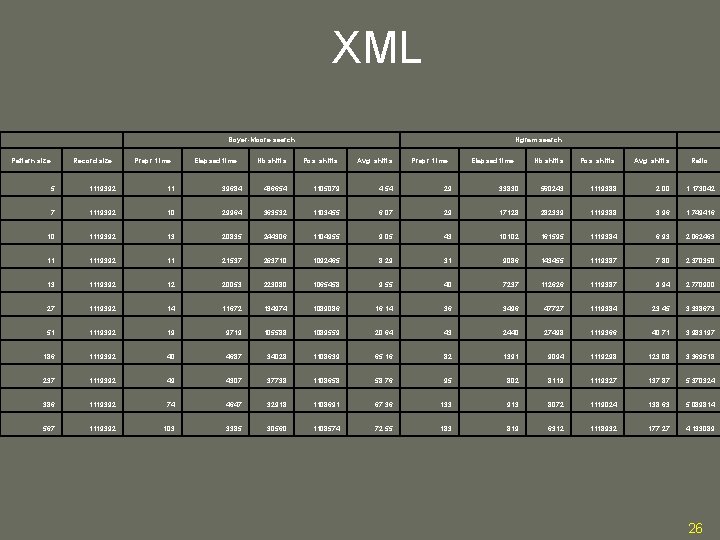
XML Boyer-Moore search Pattern size Record size Prepr. time Elapsed time Ngram search Nb shifts Pos. shifts Avg. shifts Prepr. time Elapsed time Nb shifts Pos. shifts Avg. shifts Ratio 5 1119392 11 39684 486654 1105079 4. 54 29 33830 560243 1119388 2. 00 1. 173042 7 1119392 10 29964 363532 1103455 6. 07 29 17128 282339 1119388 3. 96 1. 749416 10 1119392 13 20835 244306 1104955 9. 05 43 10102 161595 1119384 6. 93 2. 062463 11 1119392 11 21537 263710 1092465 8. 29 31 9086 143455 1119387 7. 80 2. 370350 13 1119392 12 20053 223080 1065458 9. 55 40 7237 112626 1119387 9. 94 2. 770900 27 1119392 14 11672 134974 1089086 16. 14 36 3496 47727 1119384 23. 45 3. 338673 51 1119392 19 9719 105588 1089559 20. 64 43 2440 27498 1119366 40. 71 3. 983197 186 1119392 40 4687 34028 1108639 65. 16 82 1391 9094 1119298 123. 08 3. 369518 237 1119392 49 4307 37738 1108658 58. 76 95 802 8119 1119327 137. 87 5. 370324 386 1119392 74 4647 32918 1108691 67. 36 133 913 8072 1119024 138. 63 5. 089814 567 1119392 103 3385 30560 1108574 72. 55 183 819 6312 1118932 177. 27 4. 133089 26

Related Work • Implemented in SDDS-2006 • Applies best to – longer patterns • where many jumps occur – alphabets much smaller than the size of GF used • Instead of shifts of size m in the average, one reaches almost min (K, 2 f) per shift – up to almost 256 for DNA or ASCII with GF (256) – up to almost 64 K for DNA or Unicode with GF (64 K) • instead of 4 or 25 respectively – For Boyer-Moore especially 27

Related Work • In SDDS 2006 & P 2 P or Grid System in general • Wish to hide what is searched for ? • Use the signature only based search – Usually slower since linear only 28

Conclusion • • A new pattern matching algorithm Uses algebraic signatures Preprocesses both the pattern and the string Appears particularly efficient – For databases – For longer patterns • Possibly faster in this context than any other algorithm known know • But all this are only preliminray results 29

Future Work • Performance Analysis – Theoretical • Jump Length – Median, Average… – Experimental • Actual text – Non uniform symbol distribution • DNA – Actual DNA strings 30

Future Work • Variants – Jump Table – Partial Signatures of n –grams • Symbol pi encodes the n –gram signature up to pin+1 …pi – No more XORing & Division to find this signature – Faster unsuccessful attempt to match – Approximate Match • Tolerating match errors – E. g. , and at most 1 symbol 31

Thank You for Your Attention witold. litwin@dauphine. fr 32