Pattern Matching in the streaming model Ely Porat


















- Slides: 36

Pattern Matching in the streaming model Ely Porat Google inc & Bar-Ilan University

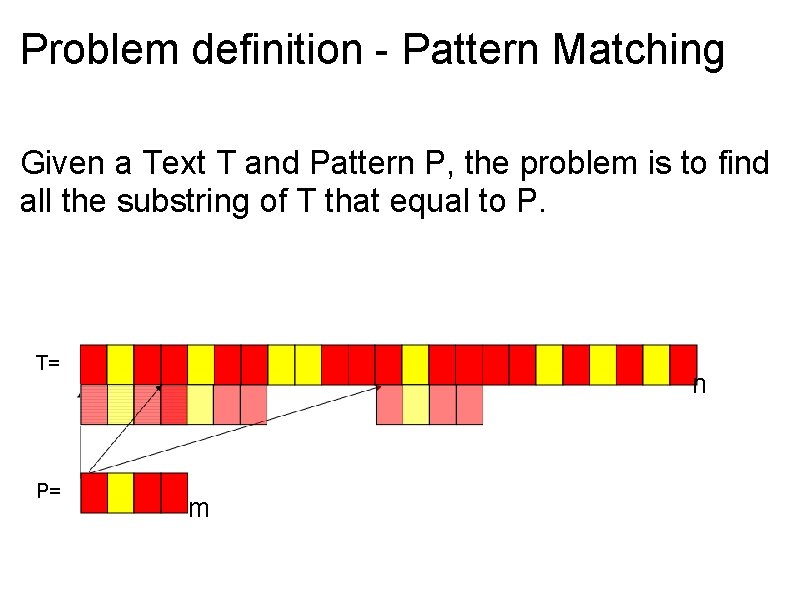
Problem definition - Pattern Matching Given a Text T and Pattern P, the problem is to find all the substring of T that equal to P. T= P= n m

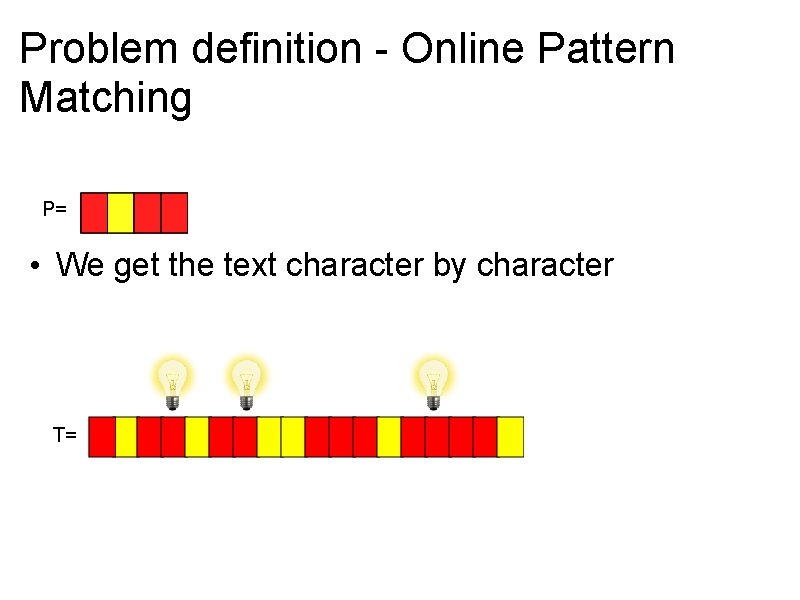
Problem definition - Online Pattern Matching P= • We get the text character by character T=

Motivation… • Stock market


Motivation. . • Espionage The rest we monitor

Motivation… • Viruses and malware Software solutions: Snort: 73. 5 Mb Clam. AV: 1. 48 Gb Using TCAMs: Snort: 680 Kb Clam. AV: 25 Mb Our solution (software): Snort: 51 Kb Clam. AV: 216 Kb

Motivation… • Monitoring internet traffic

Streaming model 250 BPS We can't store the whole input In our case we seek for algorithm which require poly(log m) space

Related work • Karp-Rabin: Randomized Algorithm for exact pattern matching • Clifford, Porat, and Porat: A black box algorithm for online approximate pattern matching o Almost any pattern matching algorithm can be converted to run online.

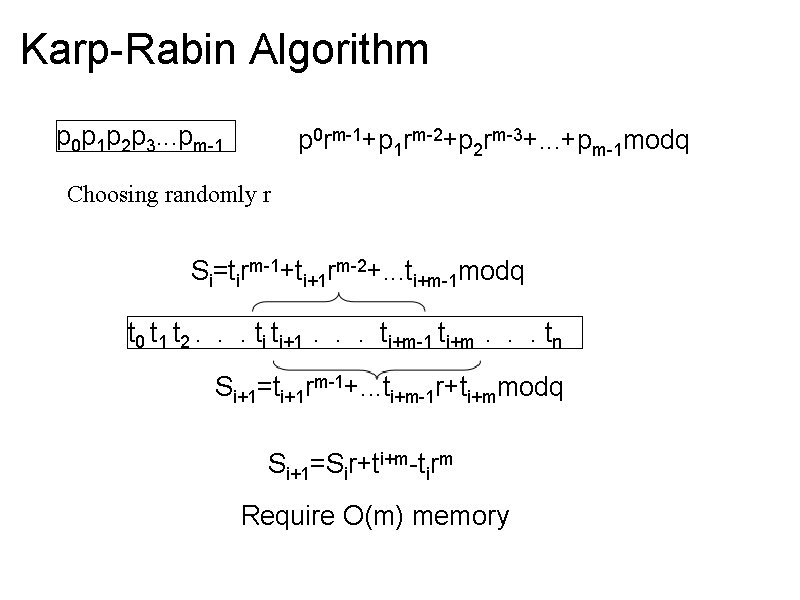
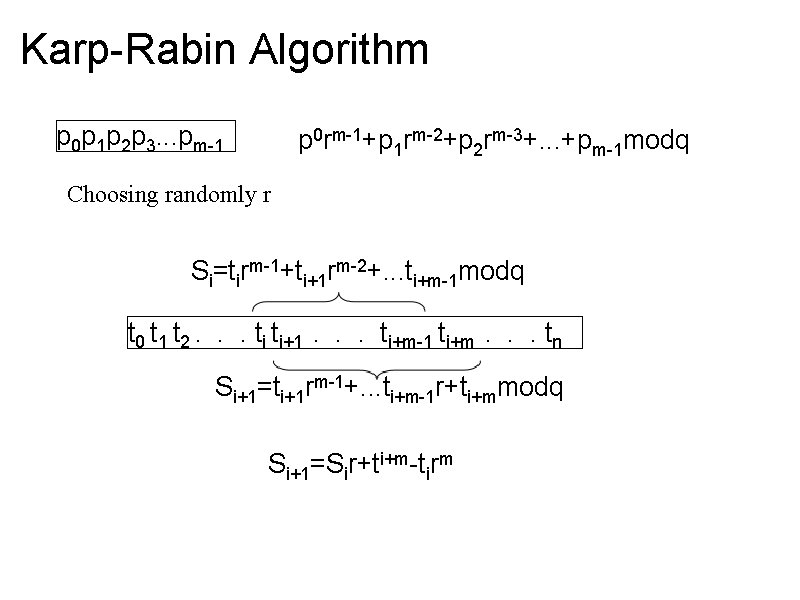
Karp-Rabin Algorithm p 0 p 1 p 2 p 3. . . pm-1 p 0 rm-1+p 1 rm-2+p 2 rm-3+. . . +pm-1 modq Choosing randomly r Si=tirm-1+ti+1 rm-2+. . . ti+m-1 modq t 0 t 1 t 2. . . ti ti+1 . . . ti+m-1 ti+m . . . tn Si+1=ti+1 rm-1+. . . ti+m-1 r+ti+mmodq Si+1=Sir+ti+m-tirm Require O(m) memory

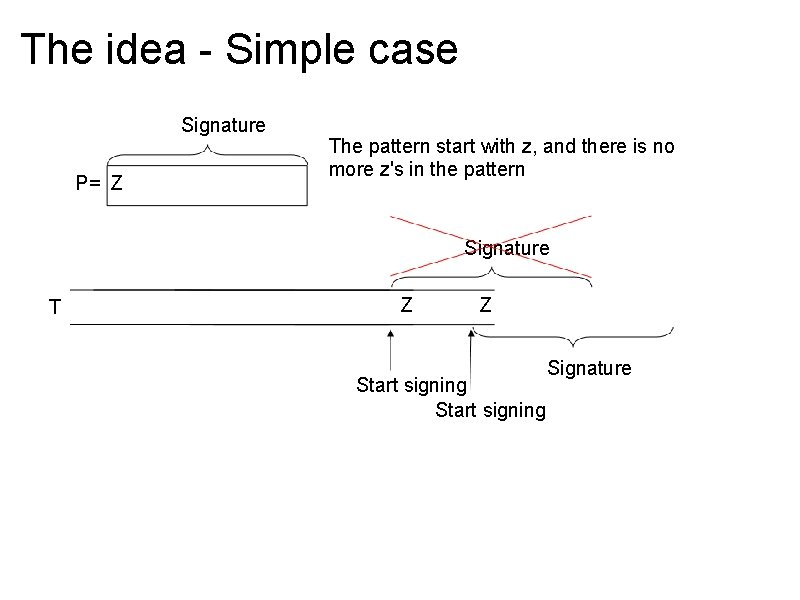
The idea - Simple case Signature P= Z The pattern start with z, and there is no more z's in the pattern Signature T Z Z Start signing Signature

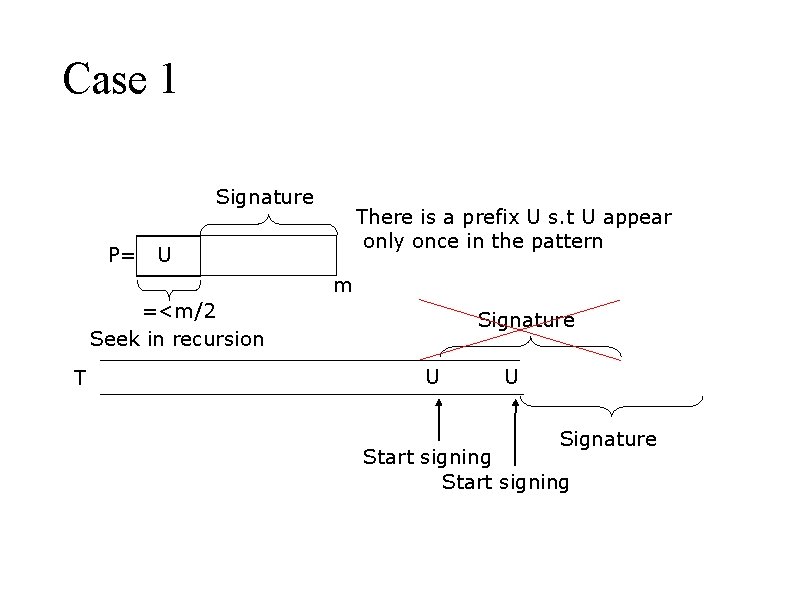
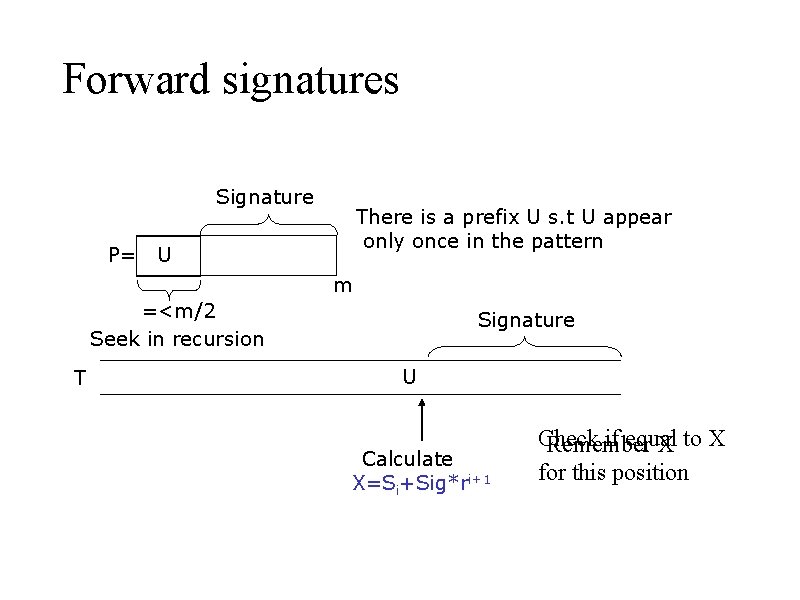
Case 1 Signature P= There is a prefix U s. t U appear only once in the pattern U m =<m/2 Seek in recursion T Signature U U Signature Start signing

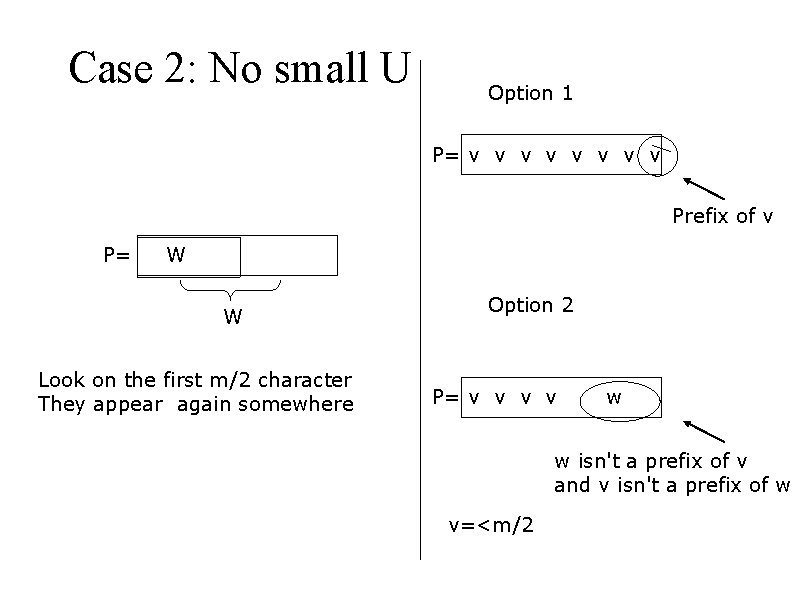
Case 2: No small U Option 1 P= v v v v Prefix of v P= W W Look on the first m/2 character They appear again somewhere Option 2 P= v v w w isn't a prefix of v and v isn't a prefix of w v=<m/2

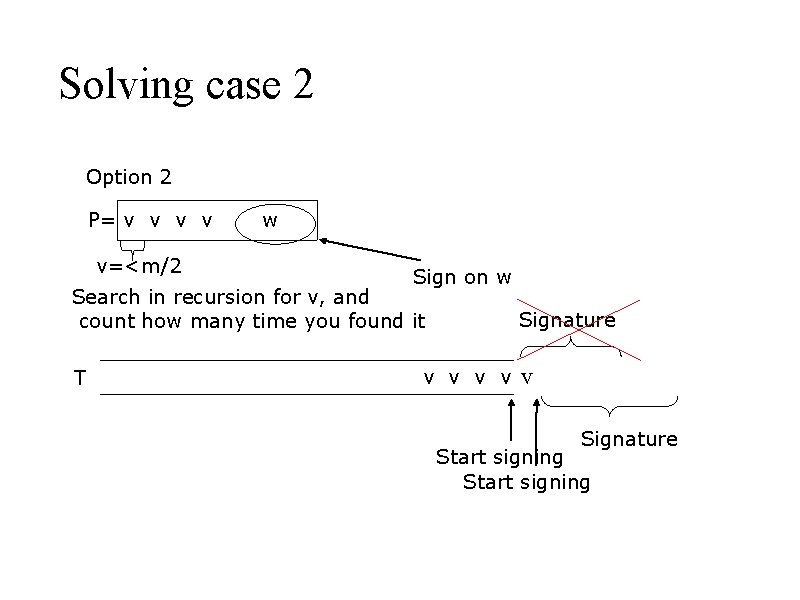
Solving case 2 Option 2 P= v v v=<m/2 w Sign on w Search in recursion for v, and count how many time you found it T Signature v v v Signature Start signing

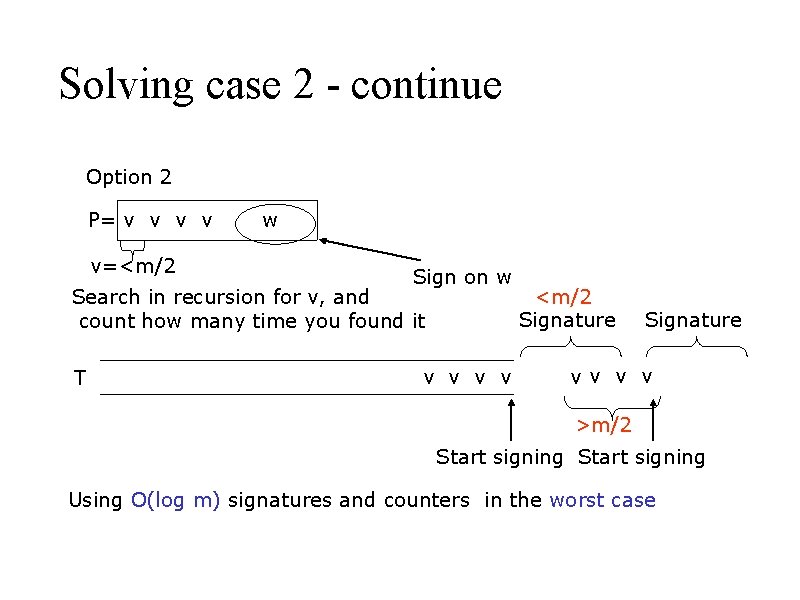
Solving case 2 - continue Option 2 P= v v v=<m/2 w Sign on w Search in recursion for v, and count how many time you found it T v v <m/2 Signature vv v v >m/2 Start signing Using O(log m) signatures and counters in the worst case

Karp-Rabin Algorithm p 0 p 1 p 2 p 3. . . pm-1 p 0 rm-1+p 1 rm-2+p 2 rm-3+. . . +pm-1 modq Choosing randomly r Si=tirm-1+ti+1 rm-2+. . . ti+m-1 modq t 0 t 1 t 2. . . ti ti+1 . . . ti+m-1 ti+m . . . tn Si+1=ti+1 rm-1+. . . ti+m-1 r+ti+mmodq Si+1=Sir+ti+m-tirm

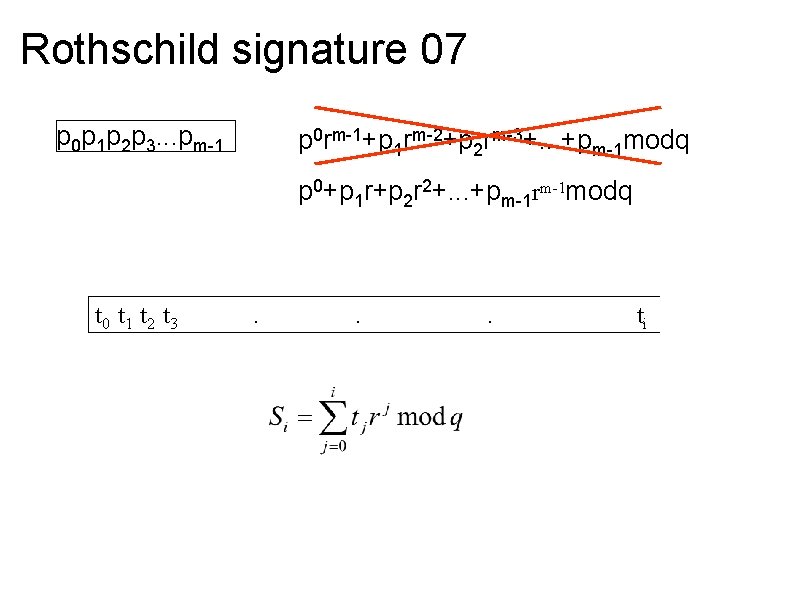
Rothschild signature 07 p 0 p 1 p 2 p 3. . . pm-1 p 0 rm-1+p 1 rm-2+p 2 rm-3+. . . +pm-1 modq p 0+p 1 r+p 2 r 2+. . . +pm-1 rm-1 modq t 0 t 1 t 2 t 3 . . . ti

Forward signatures Signature P= There is a prefix U s. t U appear only once in the pattern U m =<m/2 Seek in recursion T Signature U Calculate X=Si+Sig*ri+1 Check if equal Remember X to X for this position

Example: q=7 r=3 5 P: 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1 0, 1, 1 4 Level 1: Level 2: Level 3: T: Level 3: Level 2: Level 1: 1 ri= 264513 0 1 1 0 0 1 1 1 0 0 0 1 1 0 1 0 03326662441600000014463311 5 6 34 6 13 2 6 4 3 0 0 1 1

Worst case - time t 0 t 1 t 2 t 3 . . . Amortized O(1), but what about worst case? ti X 1 X 2 Check using hash table X 1=X 2=…=Xlogm ? ? ? Xlogm We can work in lazy approach without blowup in the memory Time: O(1)

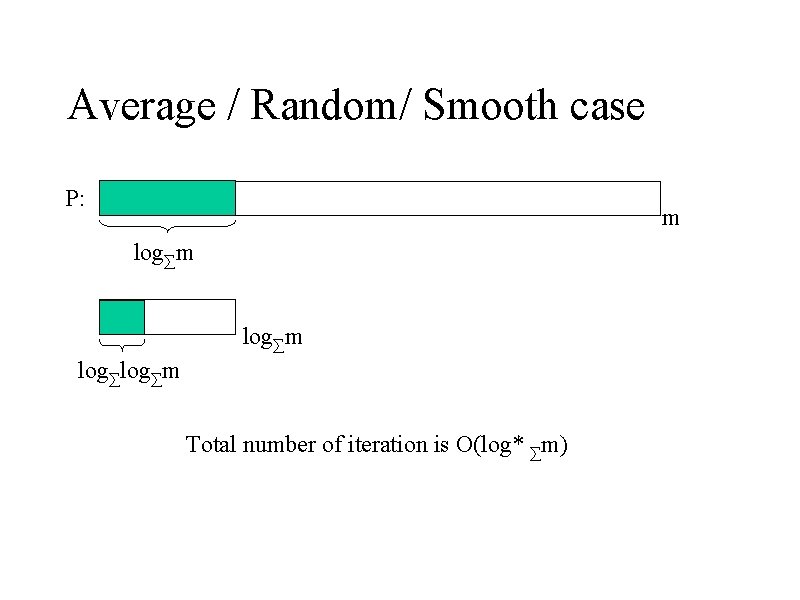
Average / Random/ Smooth case P: m log∑m Total number of iteration is O(log* ∑m)

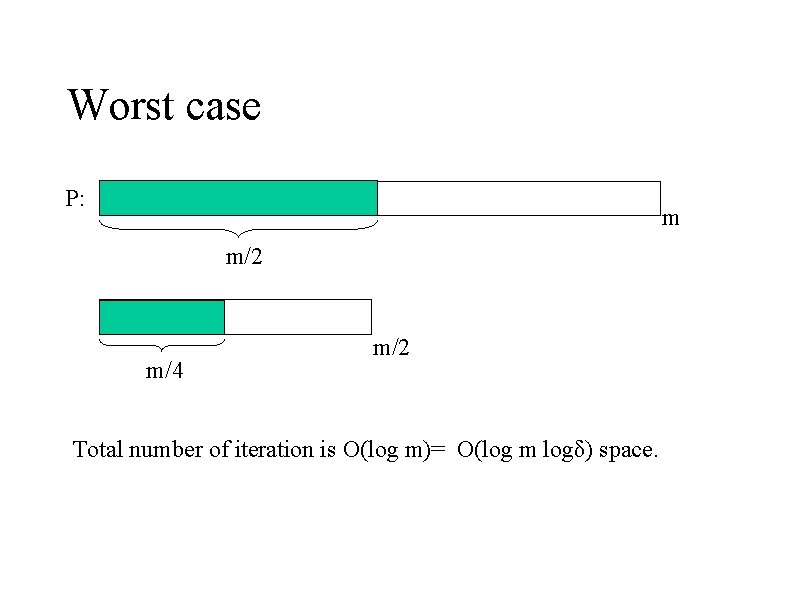
Worst case P: m m/2 m/4 m/2 Total number of iteration is O(log m)= O(log m logδ) space.

Multi-Pattern search (dictionary matching) • Given a set of patterns D={P 1, P 2, P 3, …, Pd} – The patterns can be of different length • We will want to report whenever one of the patterns appear. • Our algorithm will require O(∑i=1 dlog|Pi|) memory, and will require O(log d) time per text character.

Multi-Pattern search (dictionary matching) • Denote M=maxi |Pi| • Our algorithm will have 2 cases: – Case 1: d>M – Case 2: d<M

Case 1: d>M • In this case we can allocate an array of size M+1 t 0 t 1 t 2 t 3 . . . tl-M+1. . . tl Sl-M+1. . . Sl It is easy to maintain such a sliding window in O(1) time and O(M) memory

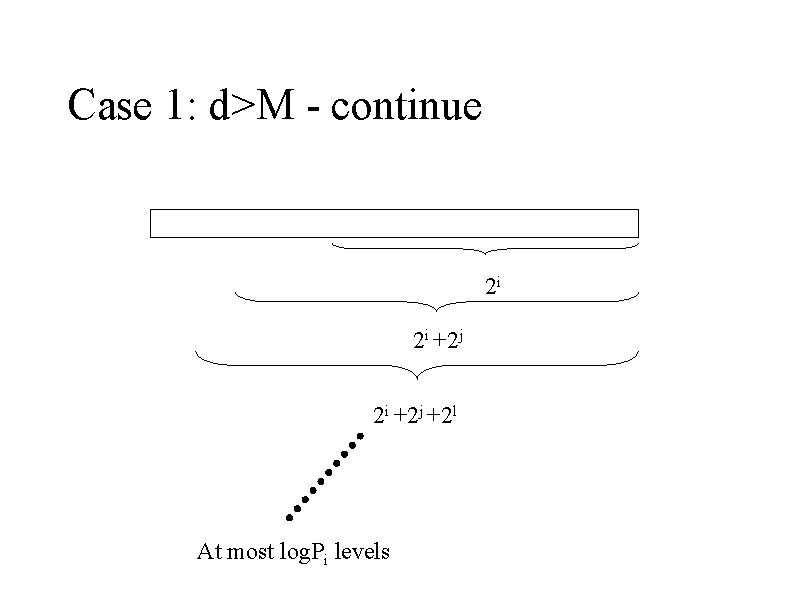
Case 1: d>M - continue Example For each Pi in D: (Pi=a 0 a 1 a 2 … ami-1) e=mi while e!=0: find j s. t 2 j=<e and 2 j+1>e e=e-2 j if e!=0 Hash. Table(Sig(aeae+1…ami)) Hash. Table(Sig(a 0 a 1…ami), matchi) Pi=a 0 a 1 a 2 … a 38 We will store in the hash table: Sig(a 7 a 6…a 38) Sig(a 3 a 4…a 38) Sig(a 1, a 2…a 38) Sig(a 0 a 1…a 38), matchi We will store at most log |Pi| points

Case 1: d>M - continue 2 i 2 i +2 j +2 l At most log. Pi levels

Case 1: d>M • In this case we can allocate an array of size M+1 t 0 t 1 t 2 t 3 . . . tl-M+1. . . tl Sl-M+1. . . Sl Notice that it take O(1) to calculate Sig(titi+1…tl)

Case 1: d>M - continue We will do binary search over the sliding window j-1 j j-1 l-2 l-2 l-2 -2 j-2 Sl-M+1 . . . Sl No Yes in the Hash. Table? Is it. Isinit. Isthe init the Hash. Table?

Case 2: d<M • In this case we will split our dictionary D into 2 dictionaries: – D 1 – all the patterns shorter then d. On this dictionary we will run case 1. – D 2 – all the patterns longer then d. We need only to deal with this case.

Case 2: d<M - continue For each Pi in D 2: Pi = a 0 a 1 a 2. . . ad-1 ad SPi=Sig(a 0 a 1…ad-1) Store in hash table SPi . . . am

Case 2: d<M - continue If Pi contain a period prefix of length more then d w. h. p won’t be SPi Pi = u u u v . . am SPi SPi We store as well the number of time we need to see SPi We will start a process which will seek for Pi only after seeing enough SPi. Therefore the minimum number of characters we have to see between 2 process of Pi is at least d.

Case 2: d<M - continue • We run the algorithm from the beginning of the lecture. • Amortized it take O(1/d) per pattern per text character. • Overall it take O(1) amortized time per text character. • By lazy approach we get O(1) time in worst case.

Open problems • Multi pattern search case 2 takes O(1) time, however case 1 takes O(logd) – Improve case 1 to be O(1) – With heuristic almost all the dictionary take O(1) time, and O(1) space per pattern. • Lower bound – We believe that single pattern search lower bound is Ώ(log m log δ) • Find more clients • Find a place for sabbatical (~1/1/2012 -30/9/2013)

Important things: • In coming events: – ICALP 2011 GT (July 3 rd, one day before ICALP) • We will have some support for students – Workshop on Sparsity and Computation, U. Mich. Aug 1 --4 • We will have some support for students – IMA: Group Testing Designs, Algorithms, and Applications to Biology Feb 13 --17 – Stringology 2012 • Find a place for sabbatical (~1/1/2012 -30/9/2013)