Pathfinding CSE 35415541 Matt Boggus Pathfinding problem statement

Pathfinding CSE 3541/5541 Matt Boggus

Pathfinding – problem statement • Finding the shortest route between two points • Motivation and comparison with steering • How to represent the environment • Lots of algorithms

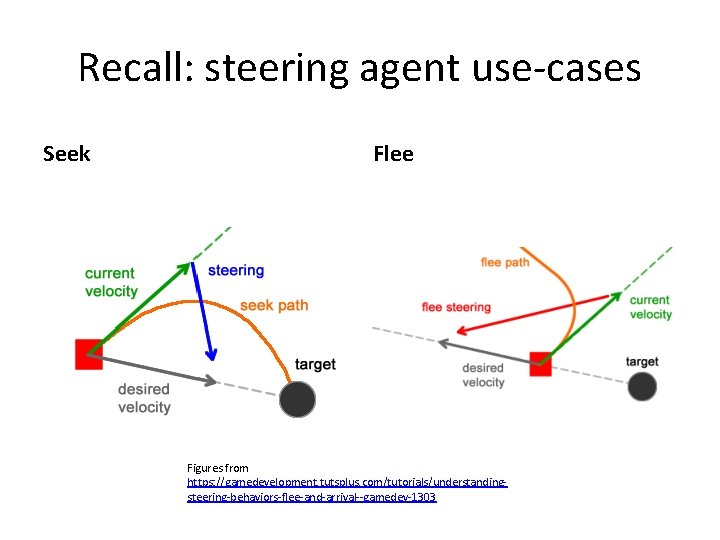
Recall: steering agent use-cases Seek Flee Figures from https: //gamedevelopment. tutsplus. com/tutorials/understandingsteering-behaviors-flee-and-arrival--gamedev-1303

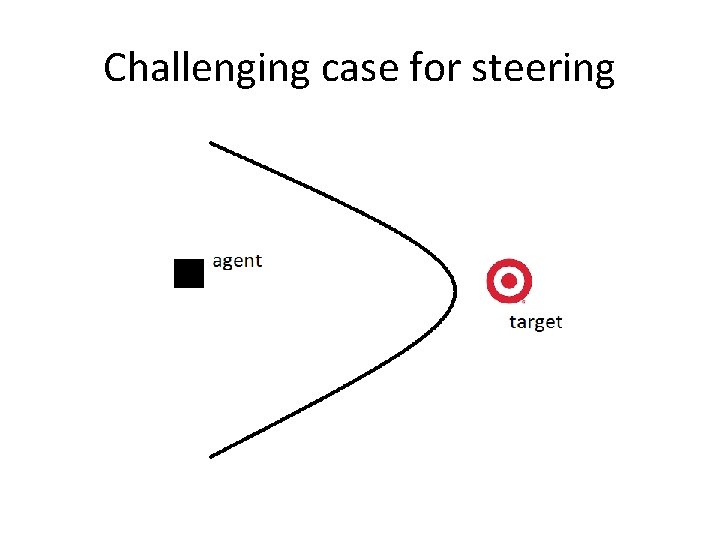
Challenging case for steering

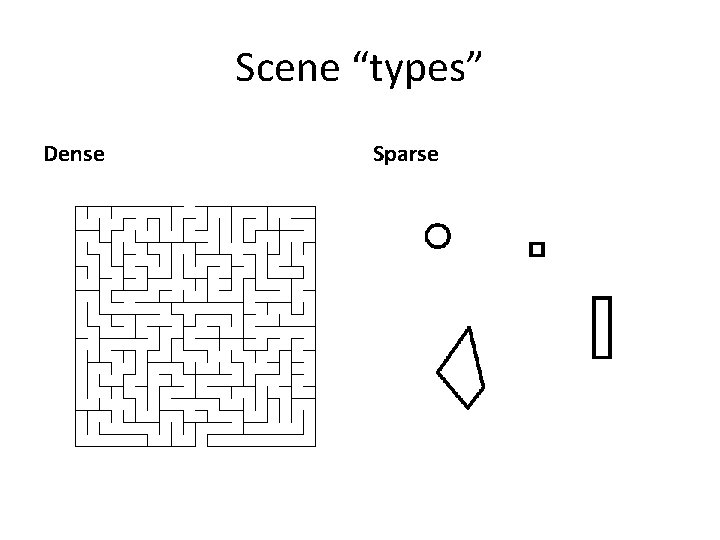
Scene “types” Dense Sparse

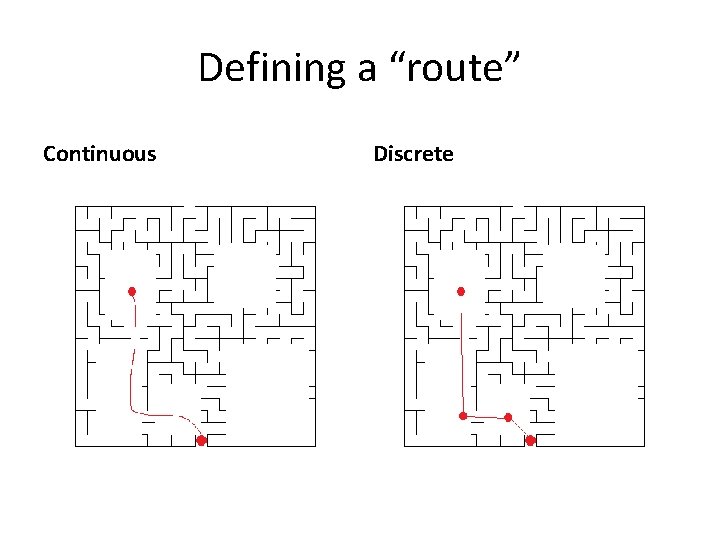
Defining a “route” Continuous Discrete

Steering with pathfinding • Coarse level of detail movement using pathfinding – Ignore small obstacles and moving objects • Fine level of detail movement using steering – Deal with objects pathfinding ignored • Ex: Steering Behaviors and A* Path Finding https: //www. youtube. com/watch? v=DXUSP_6 x. K NM

Example scene seen from above

Example scene as a grid

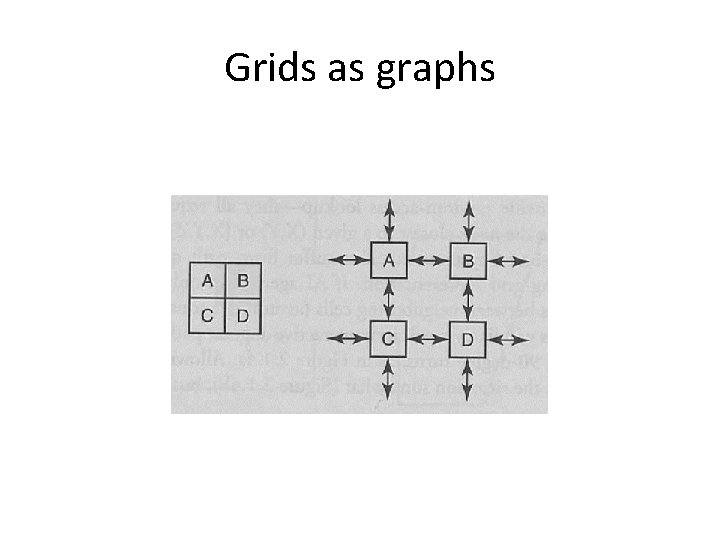
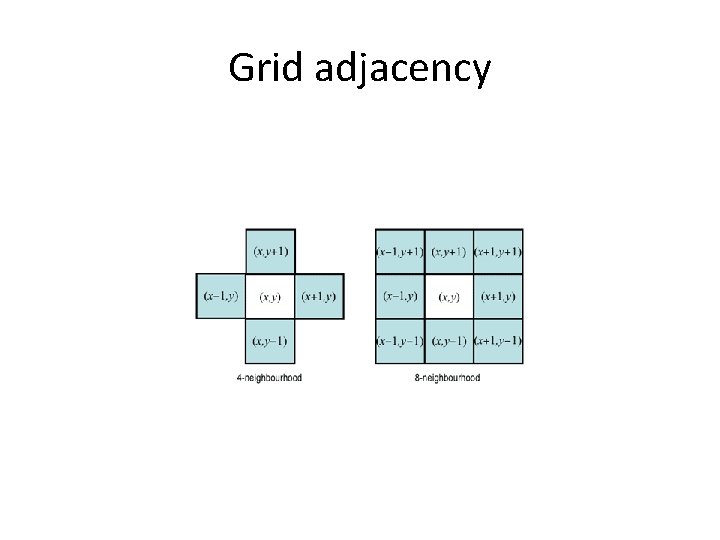
Grids as graphs

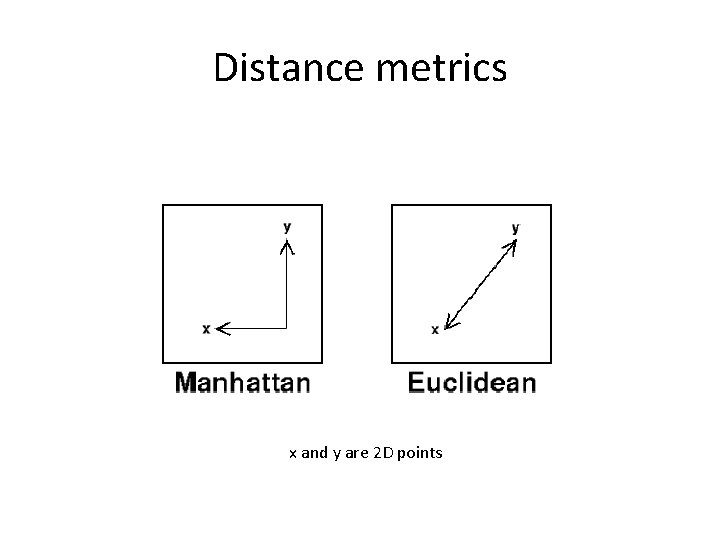
Distance metrics x and y are 2 D points

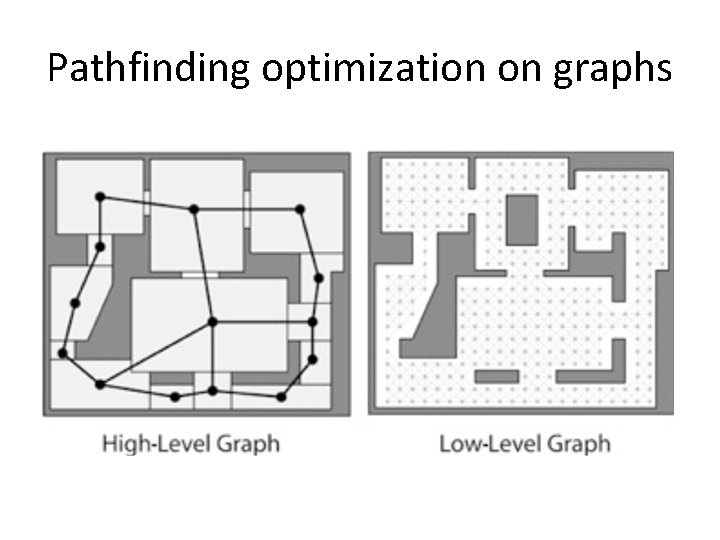
Waypoint graph

Constructing waypoint graphs Sampling discussion and boardwork

Navigation mesh

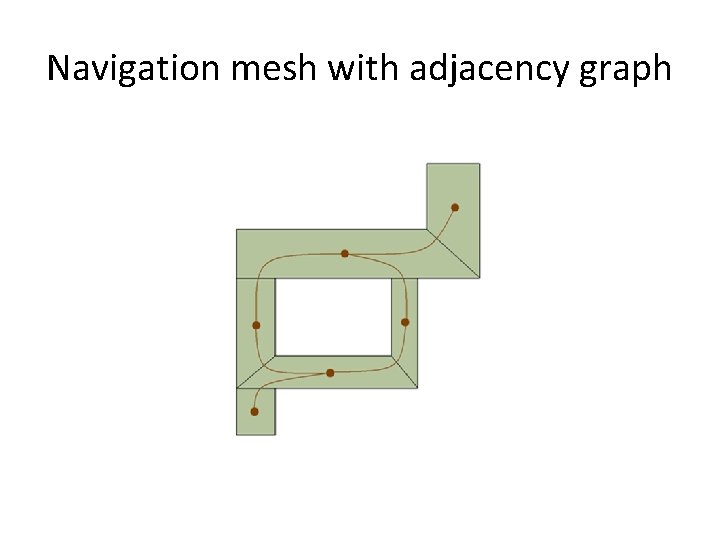
Navigation mesh with adjacency graph

Pathfinding algorithms • Random walk • • Breadth first search Best first search Dijkstra’s algorithm A* algorithm

Evaluating graph search algorithms • Resource consumption during search – CPU and memory • Quality of final path – Shortest or not • Whether it is a complete algorithm – A complete algorithm guarantees to find a path if one exists

Random walk • Agent takes a random step – If goal reached, then done – Can be implemented without searching – one step per update • If implemented as a search – Random step, saving the new position each time • Do not update/draw until the goal is reached – Add intelligence • Only step to positions where distance to goal is smaller • Stuck? With a certain probability, allow a step where distance to goal is greater

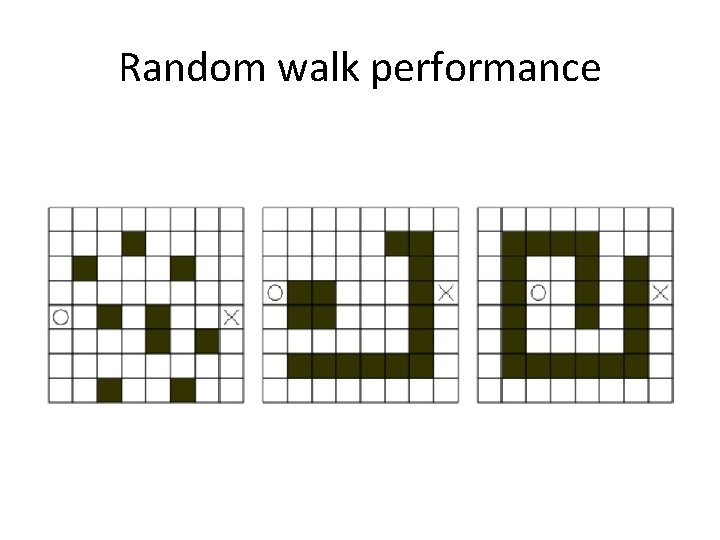
Random walk performance

Random walk properties • Not complete • Found paths are unlikely to be optimal • Consumes very little memory

Search algorithms • • Breadth-First Best-First Dijkstra’s A* (combination of Best-First and Dijkstra) • Nodes represent candidate paths • Keep track of numerous paths simultaneously

Graph search complete algorithms • Logically, these algorithms use two lists: open and closed • Open list keeps track of unexplored nodes • Examine a node on the open list: – Check to see if it is the goal – If not, check its edges to add more nodes to the open list • Each added node contains a reference to the node that explored it – Place current node on closed list (mark a field as visited) • Closed list are those that have been explored/processed and are not the goal

Implementation 1. Create start point node and push onto open list 2. While open list is not empty A. Pop node from open list (call it current. Node) B. If current. Node is the goal, break from step 2 C. Create new nodes (successors nodes) for cells around current. Node and push them onto open list D. Put current. Node onto closed list // How to compute the solution path?

Node selection • Breadth-First processes the node that has been waiting the longest – Uses a queue • Best-First processes the one that is closest to the goal – Uses a priority queue –node value is distance to goal • Dijkstra’s processes the one that is the cheapest to reach from the start cell – Uses a priority queue – node value is lowest cost from the start • A* chooses a node that is cheap and close to the goal – Uses a priority queue – node value is a combination of Best-First and Dijkstra’s

Breadth first search

Breadth-first search as building a tree Boardwork partial example for previous slide Search starts at (6, 3) Goal is at (9, 3)

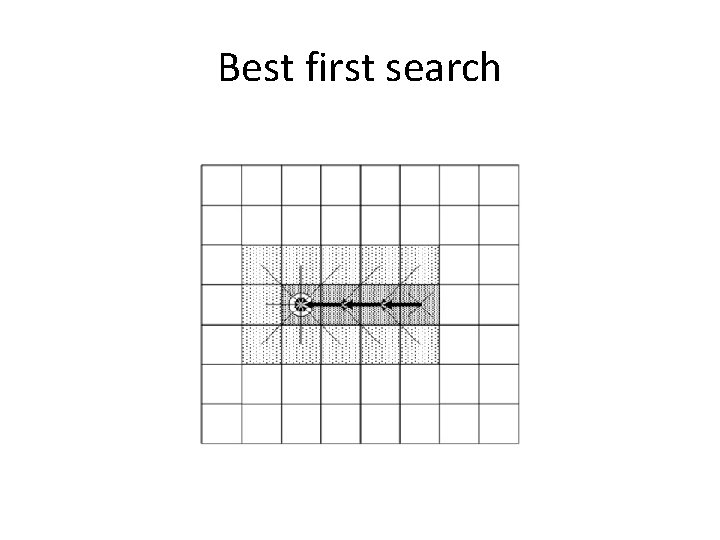
Best first search

Suboptimal best first search

Dijkstra’s algorithm • Disregards distance to goal – Keeps track of the cost of every path – No guessing / no search heuristic • Computes accumulated cost paid to reach a node from the start • Uses the cost (called the given cost) as a priority value to determine the next node that should be brought out of the open list

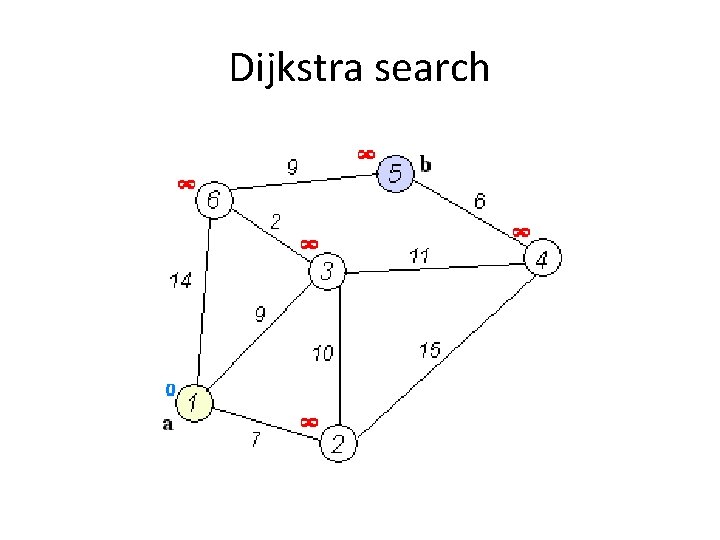
Dijkstra search

A* algorithm • Admissible heuristic function that never overestimates the true cost • To order the open list, use – Heuristic cost – estimated cost to reach the goal – Given cost – cost to reach node from the start Final Cost = Given Cost + (Heuristic Cost * Heuristic Weight)

Heuristic weight • Final Cost = Given Cost + (Heuristic Cost * Heuristic Weight) • Heuristic weight (hw) controls the emphasis on the heuristic cost versus the given cost – By definition, hw > 0 – If hw=0, final cost will be the given cost (equal to cost from Dijkstra’s) – As hw increases, final cost behaves more like Best. First cost, but never underestimates cost

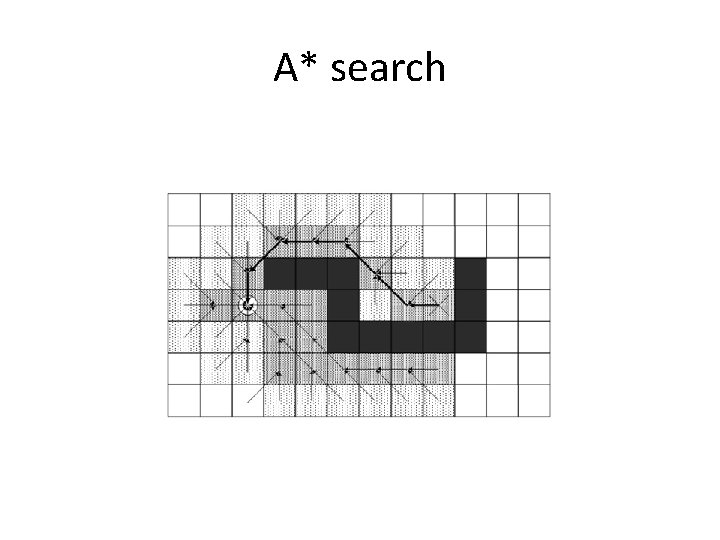
A* search

A* and Dijkstra comparison

NEXT STEPS: MULTI-AGENT AND OPTIMIZATION

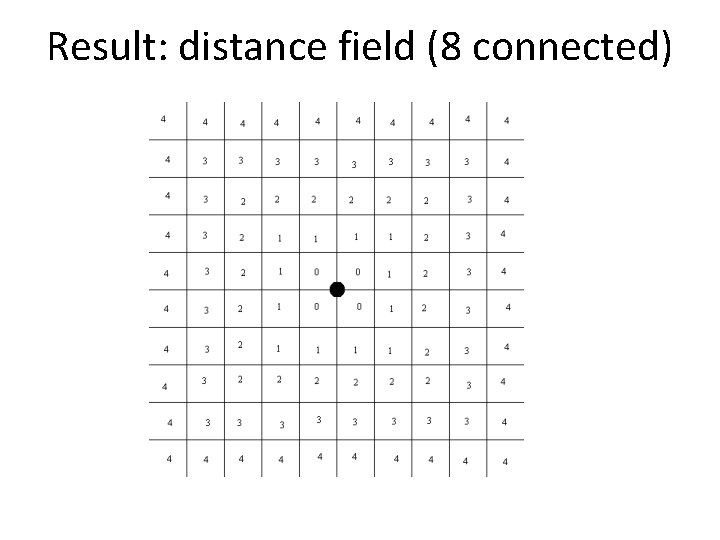
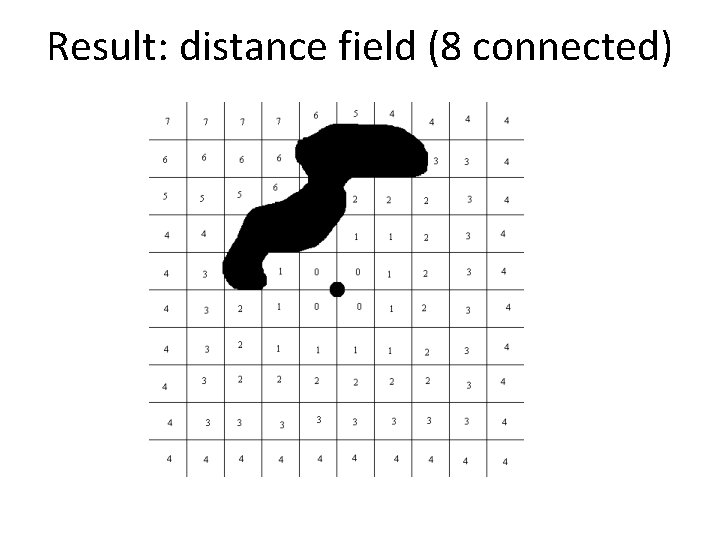
Distance-field • Represent environment using a grid of scalars, each represents distance to goal • int grid[x, y] – Initial values: • Intersect with goal, grid[x, y] = 0 • For impassable grid cells, grid[x, y] = -1 • Everywhere else, grid[x, y] = INFINITY – After the search: • grid[x, y] = distance from start, or -1 if impassable, or INFINITY if unreachable from start

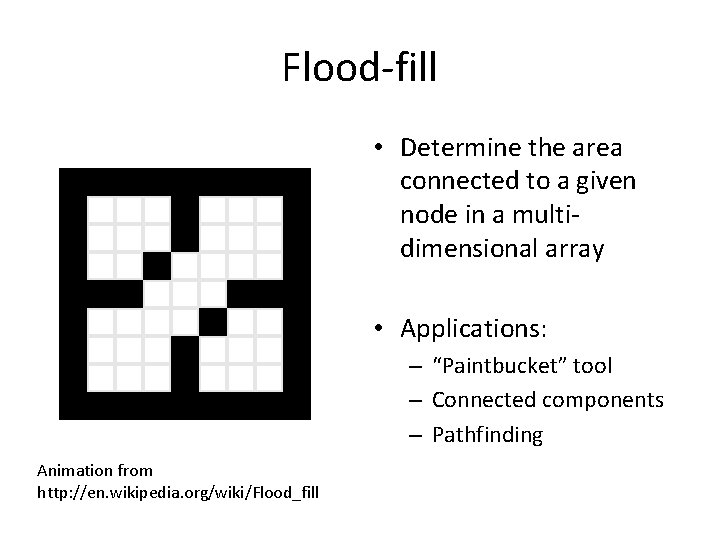
Flood-fill • Determine the area connected to a given node in a multidimensional array • Applications: – “Paintbucket” tool – Connected components – Pathfinding Animation from http: //en. wikipedia. org/wiki/Flood_fill

Flood-fill with varying value Flood-fill (x, y, value, grid) { if(x < 0 || y < 0 || x >= XSIZE || y >= YSIZE) return; if(grid[x, y] == -1 || grid[x, y] <= value) return; grid[x, y] = value; Flood-fill(x-1, y, value+1, grid); Flood-fill(x+1, y, value+1, grid); Flood-fill(x, y+1, value+1, grid); Flood-fill(x, y-1, value+1, grid); }

Queue vs. Stack Flood-fills Animations from http: //en. wikipedia. org/wiki/Flood_fill

Grid adjacency

Result: distance field (8 connected)

Result: distance field (8 connected)

Pathfinding optimization on graphs

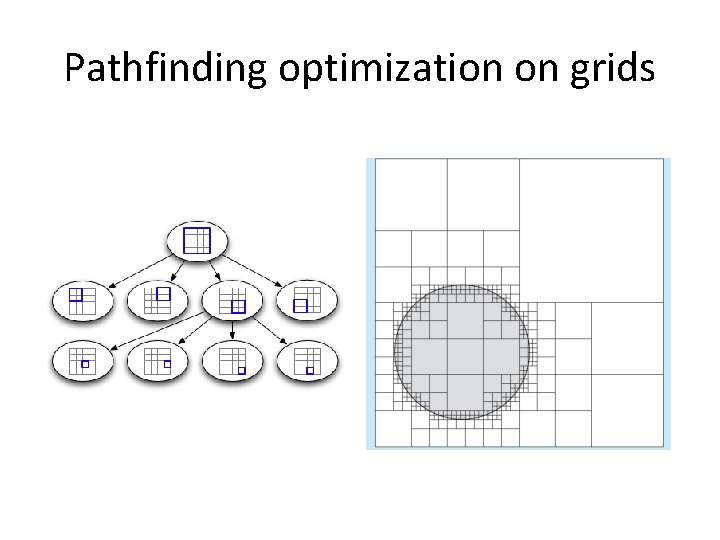
Pathfinding optimization on grids

Summary • Motivation for pathfinding as an alternative to steering agents • • • Random Walk Breadth-First Search Best-First Search Dijkstra’s A* Search

More reading on pathfinding • Amit’s A* Pages http: //theory. stanford. edu/~amitp/Game. Prog ramming/ • Beginner’s guide to pathfinding http: //aidepot. com/Tutorial/Path. Finding. html

ADDITIONAL SLIDES (MOST WORKED INTO EARLIER SLIDESETS)

Random trace • Agent moves towards goal – If goal reached, then done – If obstacle • Trace around the obstacle clockwise or counterclockwise (pick randomly) until free path towards goal • Repeat procedure until goal reached

Recursive Flood-fill code Flood-fill (x, y, value, grid) { if(x < 0 || y < 0 || x >= XSIZE || y >= YSIZE) return; if(grid[x, y] == -1 || grid[x, y] == value) return; grid[x, y] = value; Flood-fill(x-1, y, value, grid); Flood-fill(x+1, y, value, grid); Flood-fill(x, y+1, value, grid); Flood-fill(x, y-1, value, grid); } Note: method is prone to stack overflow

Iterative Flood-fill algorithm Flood-fill (x, y, value, grid) { Set Q to the empty queue Add position(x, y) to Q While Q is not empty { Dequeue position p if (p. x or p. y out of bounds) continue; if (grid[p. x, p. y] == -1 || grid[p. x, p. y] == value) continue; grid[p. x, p. y] = value; Enqueue (p. x-1, p. y); Enqueue (p. x+1, p. y); Enqueue (p. x, p. y-1); Enqueue (p. x, p. y+1); }

Mazes Maze taken from Image-guided maze construction, Xu and Kaplan 2007, Siggraph

Simple mazes – binary grid • Matrix of booleans • ex: 21 x 21 • Arbitrary mapping: – True = black pixel = wall – False = white pixel = open space

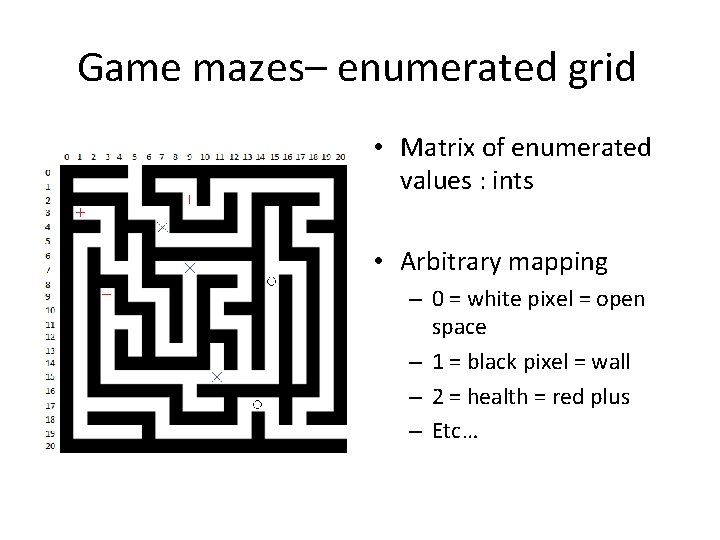
Game mazes– enumerated grid • Matrix of enumerated values : ints • Arbitrary mapping – 0 = white pixel = open space – 1 = black pixel = wall – 2 = health = red plus – Etc…

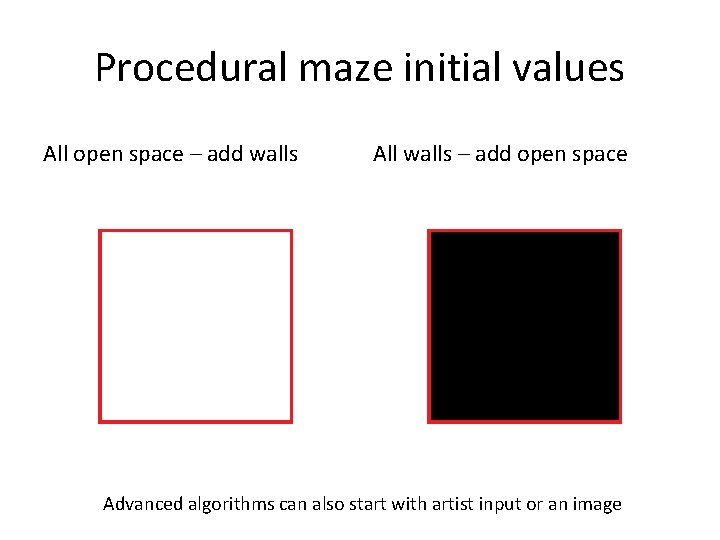
Procedural maze initial values All open space – add walls All walls – add open space Advanced algorithms can also start with artist input or an image

Maze generation – start with all walls • Randomized depth first search – Mark current node as visited – Make list of neighbors, pick one randomly – If new node is not marked as visited, remove the wall between it and its parent – Recurse

Maze generation – start with all walls • Randomized Kruskal's algorithm – Randomly select a wall that joins two unconnected open areas, and merge them – For an n x n grid there are initially n 2 open areas, one per grid cell • Randomized Prim's algorithm – Randomly pick a starting point – Keep track of walls on the boundary of the maze – Randomly select a wall that “grows” the maze

Examples Animation examples from http: //en. wikipedia. org/wiki/Maze_generation_algorithm