path root parent children leaf subtree visiting traversing

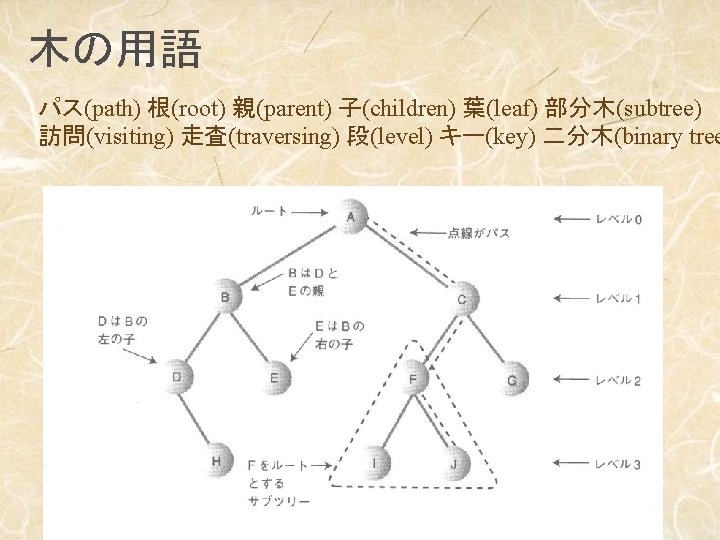
木の用語 パス(path) 根(root) 親(parent) 子(children) 葉(leaf) 部分木(subtree) 訪問(visiting) 走査(traversing) 段(level) キー(key) 二分木(binary tree

Nodeクラスの表現 class Node{ int Idata; 　　　　　 //キーとなるデータ float f. Data; 　　　 //その他のデータ node left. Child; 　 //左の子 node right. Child; 　//右の子 class Node{ 　Person p 1; //Personオブジェクトへの参照 　node left. Child; 　 //左の子 node right. Child; 　//右の子 class Person{ int i. Data; float f. Data; public void display() { …. } }

Treeクラスの表現 class Tree[ private Node root; public void find(int key){ … } public void insert(int id; float fd){ … } public void delete(int id){ … } …. . }

Tree. Appクラスの表現 class Tree. App{ public static void main(String[] args){ Tree the. Tree = new Tree; the. Tree. insert(50, 1. 5); the. Tree. insert(25, 1. 7); the. Tree. insert(75, 1. 9); node found = the. Gree. find(25); if (found != NULL) System. out. println(“Found the node with key 25); else Wystem. out. println(“Could not find node with key 25”); } }

節（ノード）探索のプログラム public Node find (int key) { Node current = root; //根（ルート）から出発 while (current. i. Data != key) { if (key < current. i. Data) current = current. left. Child; else current = current. right. Child; if ( current == null) return null; //見つからなかった } return current; //見つかった }

節（ノード）の挿入プログラム public void insert(int id, float fd){ Node new. Node = new Node(); //新節生成 newnode. idata = id; else { new. Node. data = fd; current = current. right. Child; if (rood == null) root = new. Node; if (current == null) { else { //根に節がない parent. right. Child = new. Node; Node current = root; 　　　　　//根から出発 return; Node parent; } while (true) { } parent = current; } if (id < current. i. Data) { } current = current. left. Child; } if (current == null) { parent. left. Child = new. Node; return; } }

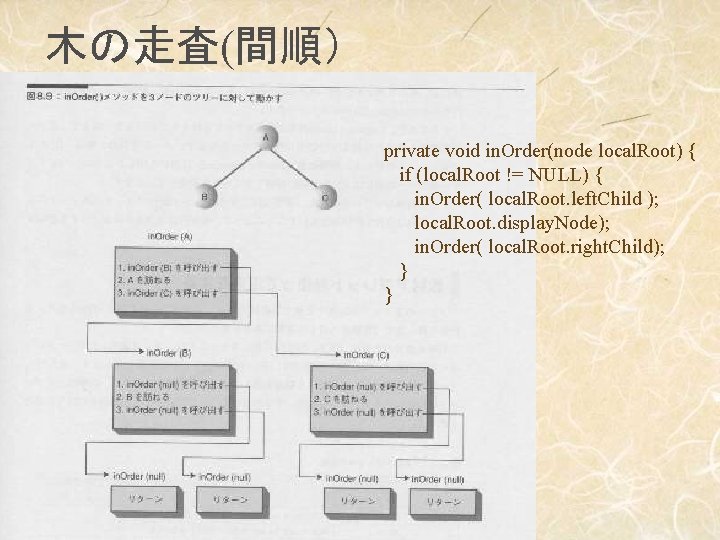
木の走査(間順） private void in. Order(node local. Root) { if (local. Root != NULL) { in. Order( local. Root. left. Child ); local. Root. display. Node); in. Order( local. Root. right. Child); } }

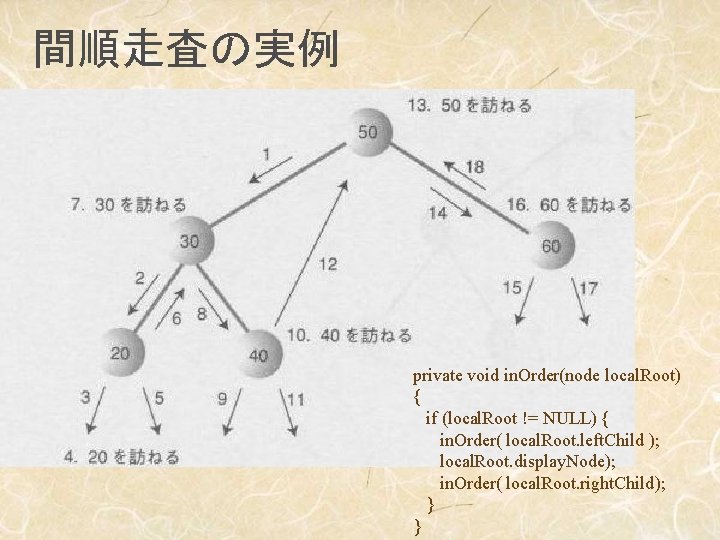
間順走査の実例 private void in. Order(node local. Root) { if (local. Root != NULL) { in. Order( local. Root. left. Child ); local. Root. display. Node); in. Order( local. Root. right. Child); } }

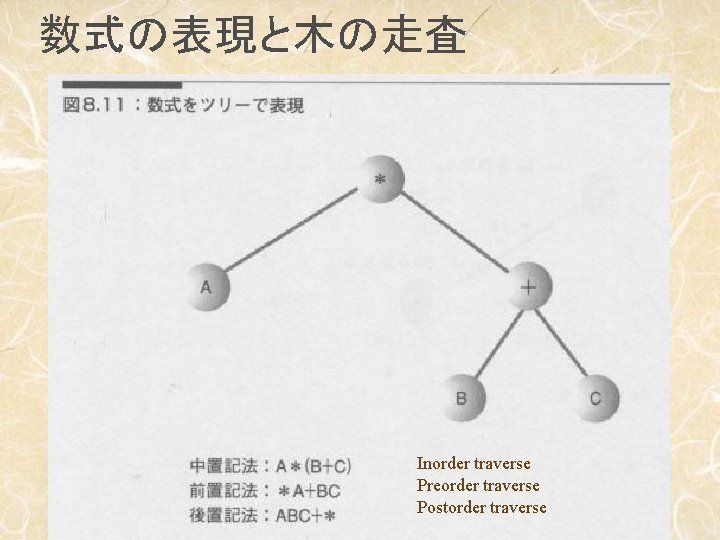
数式の表現と木の走査 Inorder traverse Preorder traverse Postorder traverse

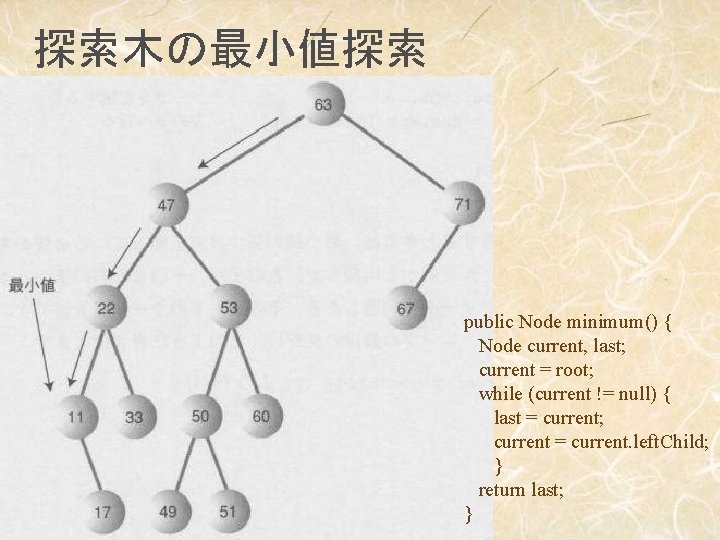
探索木の最小値探索 public Node minimum() { Node current, last; current = root; while (current != null) { last = current; current = current. left. Child; } return last; }