Path Partition for Graphs With Special Blocks September

Path Partition for Graphs With Special Blocks 潘俊杰 September 2005

Outline n n n Introduction Motivation Previous results Main result Future work

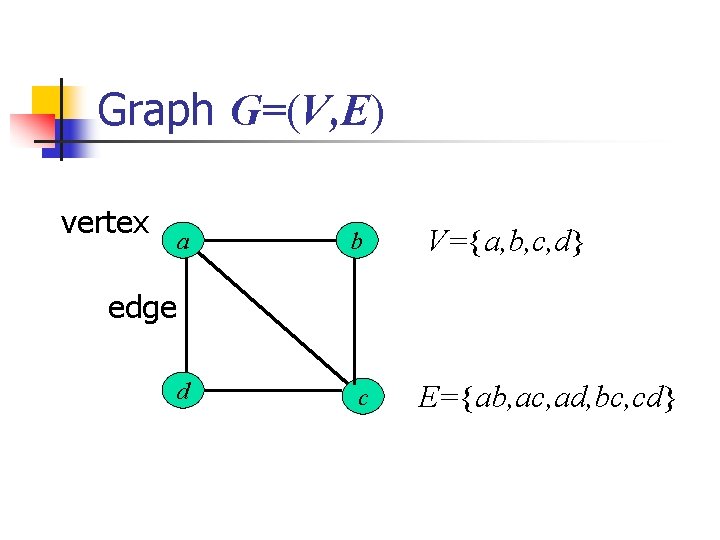
Graph G=(V, E) vertex a b d c V={a, b, c, d} edge E={ab, ac, ad, bc, cd}

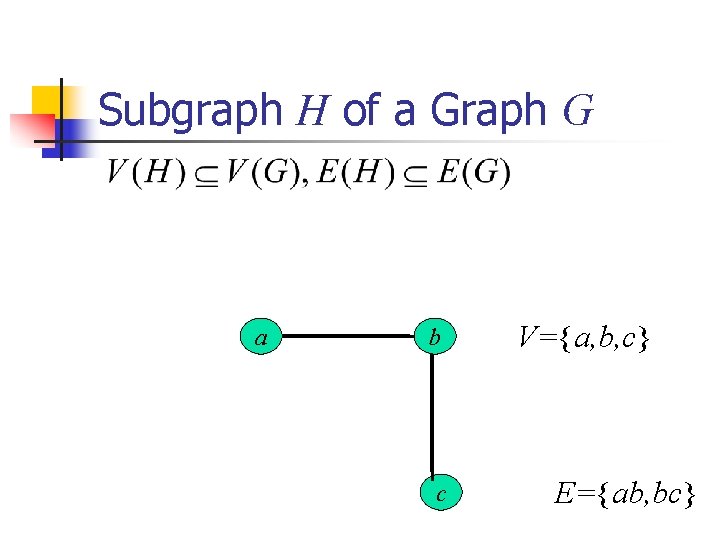
Subgraph H of a Graph G a b c V={a, b, c} E={ab, bc}

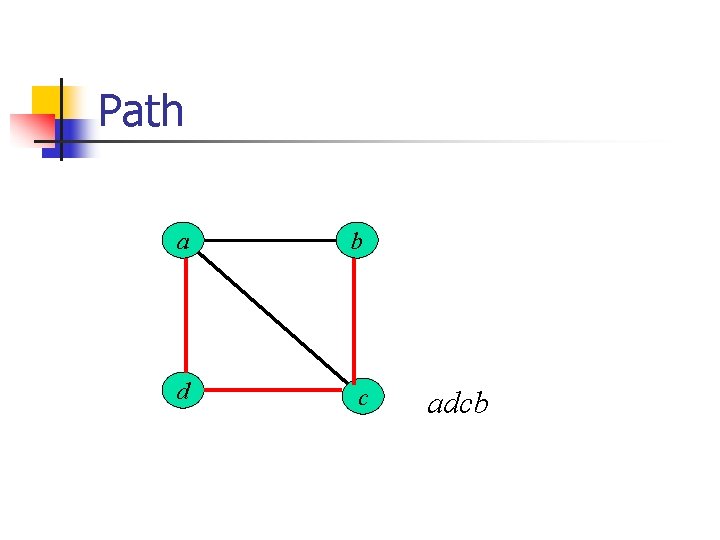
Path a b d c adcb

Path-partition A path partition of a graph is a collection of vertex-disjoint paths that cover all vertices of the graph.

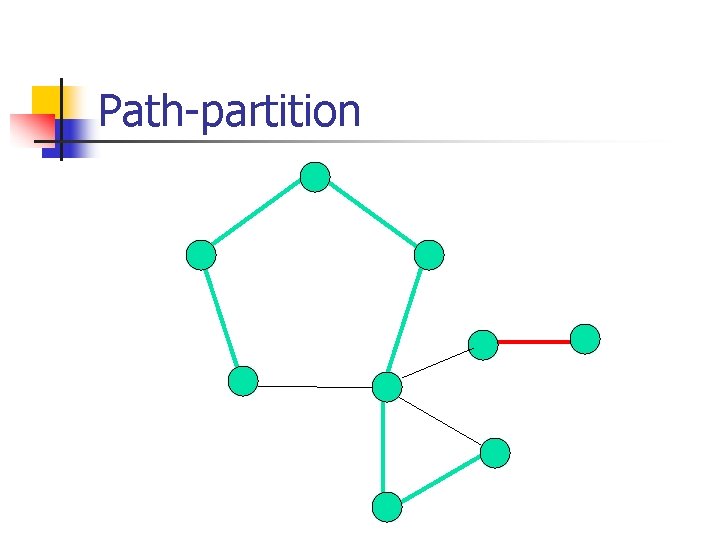
Path-partition

Path-partition Number p(G) The path-partition problem is to find the path-partition number p(G) of a graph G, which is the minimum cardinality of a path partition of G.

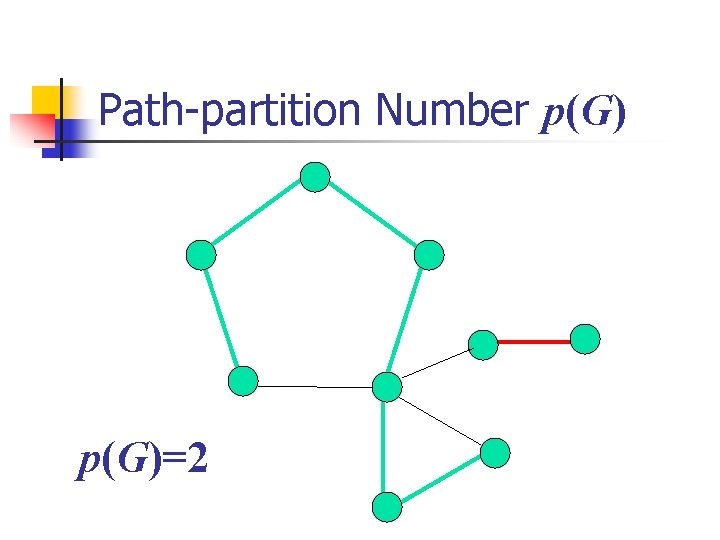
Path-partition Number p(G)=2

Cycle

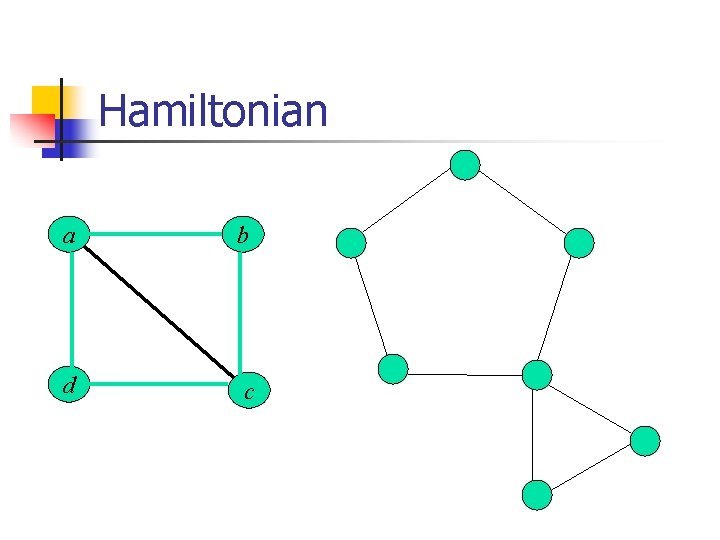
Hamiltonian a b d c

Complete Graph Kn

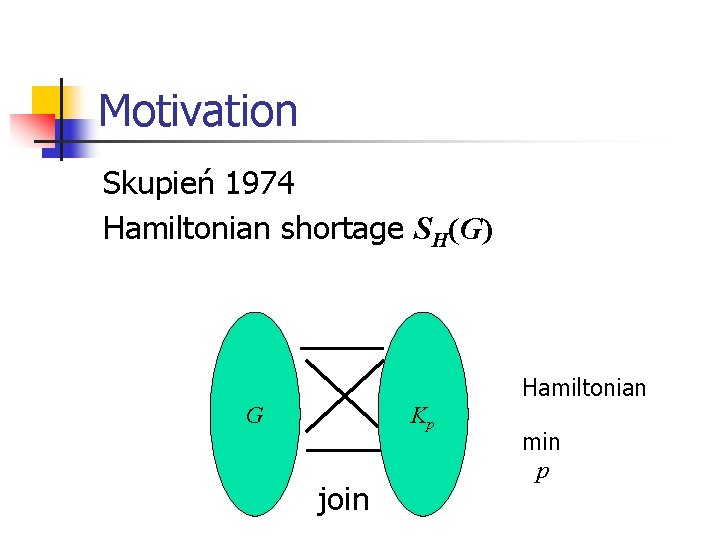
Motivation Skupień 1974 Hamiltonian shortage SH(G) Hamiltonian G Kp join min p

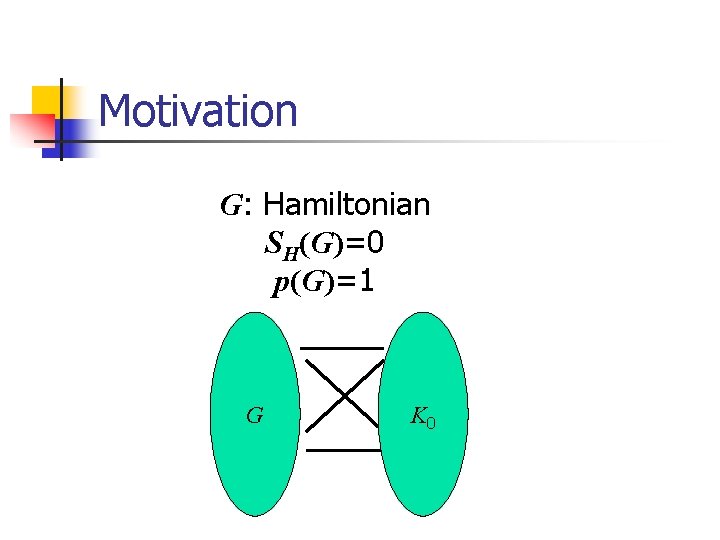
Motivation G: Hamiltonian SH(G)=0 p(G)=1 G K 0

Motivation G : K 1 SH(G)=2 p(G)=1 K 2

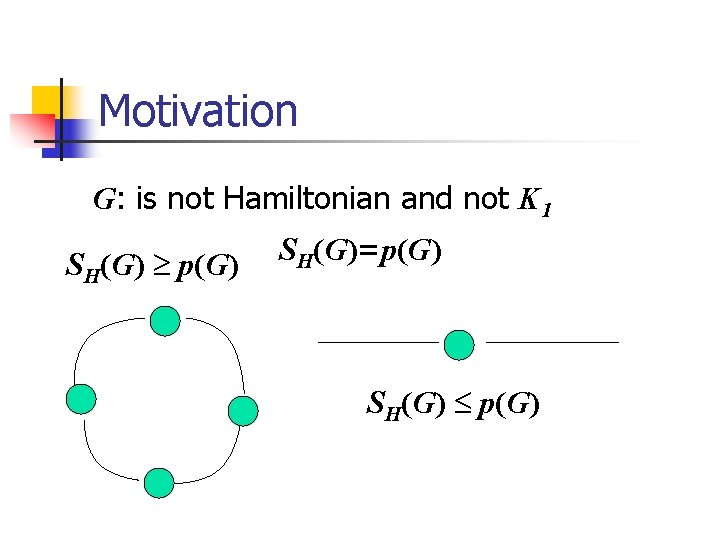
Motivation G: is not Hamiltonian and not K 1 SH(G) p(G) SH(G)=p(G) SH(G) p(G)

Previous Results Algorithmic view NP-complete Polynomial-time algorithm

Question Is the path-partition problem is NPcomplete for general graphs?

NP-Complete As the Hamiltonian path problem is NP-complete for general graphs, so is the path-partition problem.

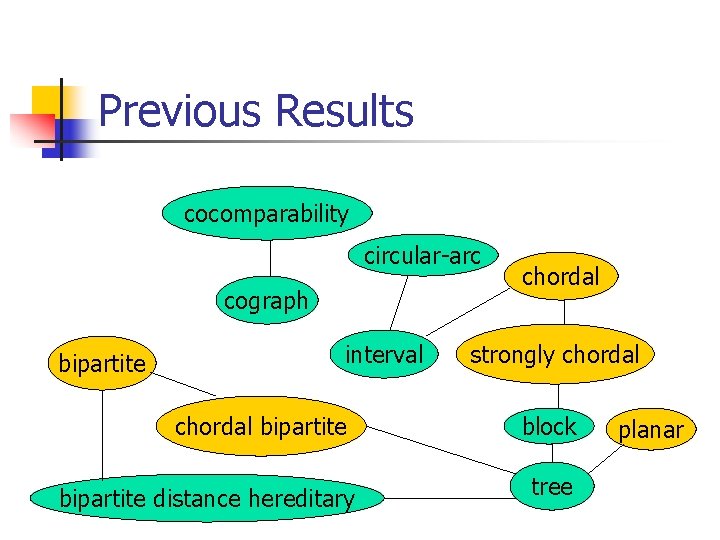
Previous Results cocomparability circular-arc cograph bipartite interval chordal bipartite distance hereditary chordal strongly chordal block tree planar

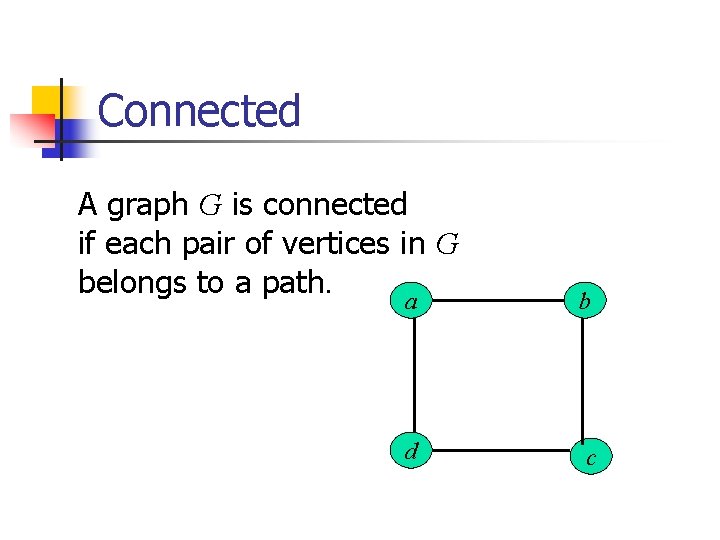
Connected A graph G is connected if each pair of vertices in G belongs to a path. a d b c

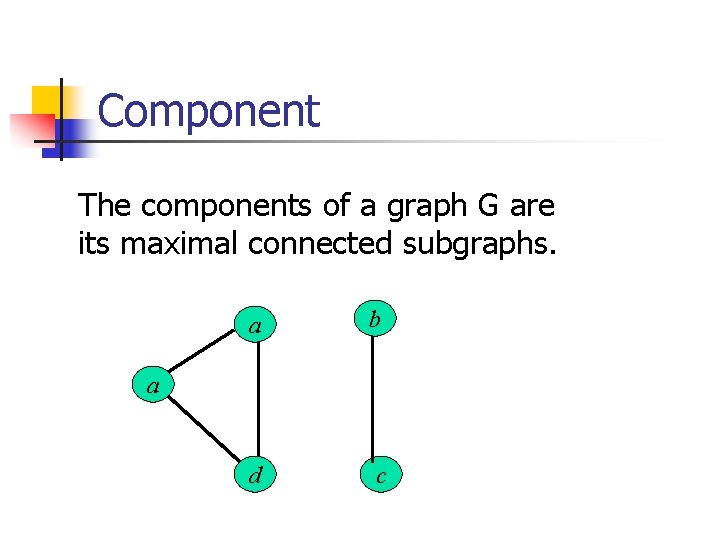
Component The components of a graph G are its maximal connected subgraphs. a b d c a

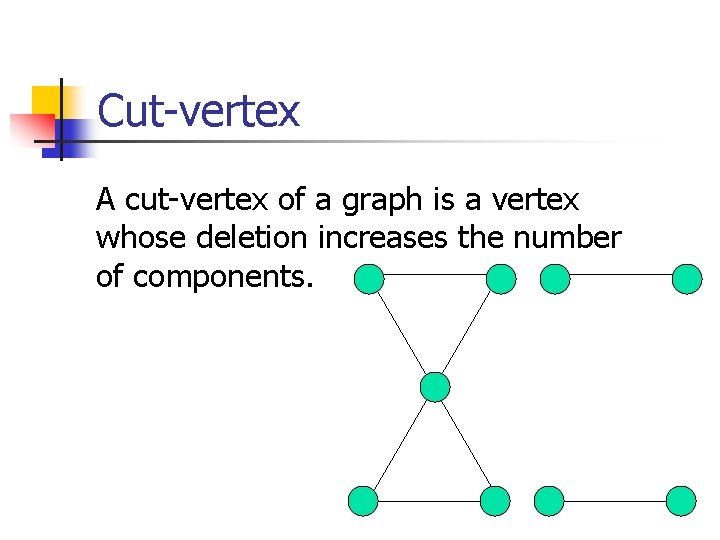
Cut-vertex A cut-vertex of a graph is a vertex whose deletion increases the number of components.

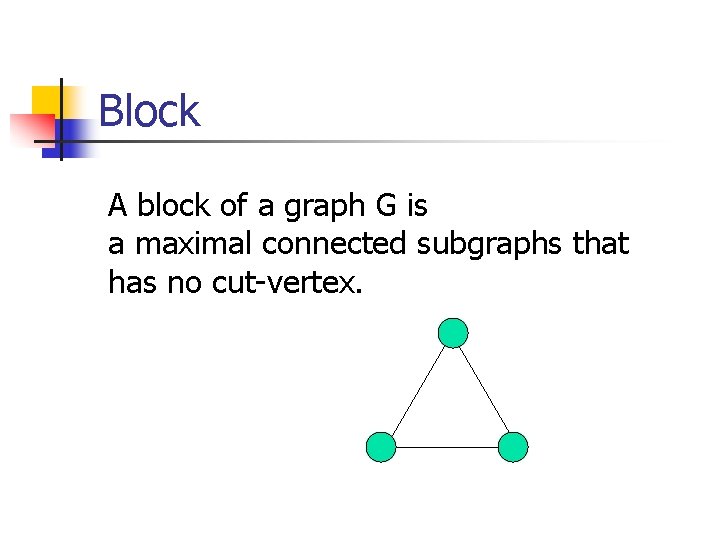
Block A block of a graph G is a maximal connected subgraphs that has no cut-vertex.

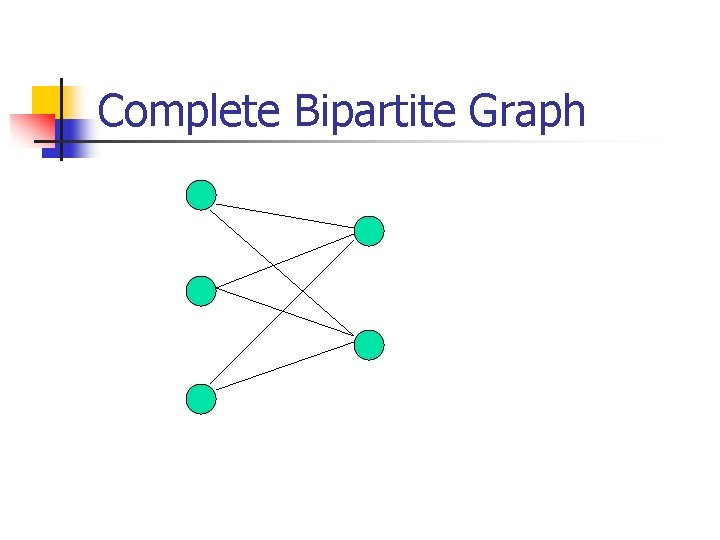
Complete Bipartite Graph

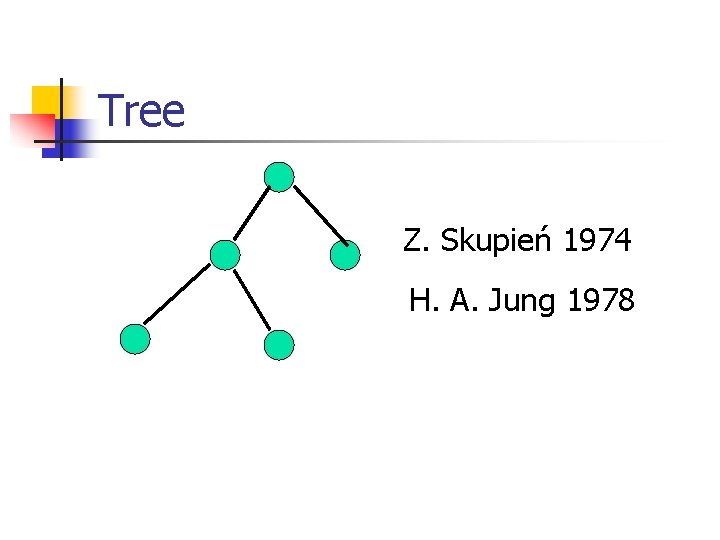
Tree Z. Skupień 1974 H. A. Jung 1978

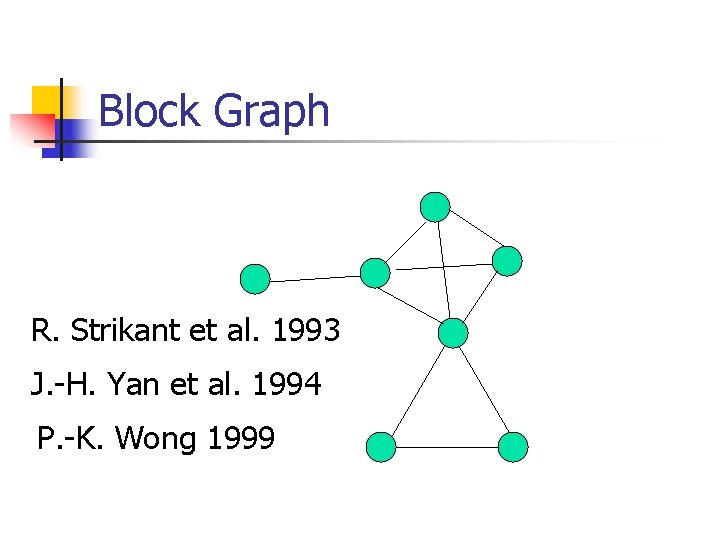
Block Graph R. Strikant et al. 1993 J. -H. Yan et al. 1994 P. -K. Wong 1999

Our Result Graphs whose blocks are complete graphs, cycles or complete bipartite graphs O(|V|+|E|)-time algorithm

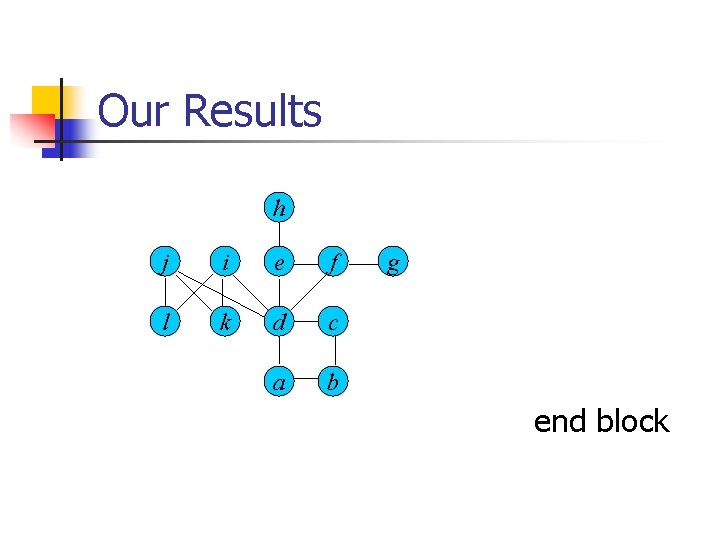
Our Results h j i e f l k d c a b g end block

f-path partition f: V(G) {0, 1, 2, 3} n f-path partition: P: collection of vertex-disjoint paths 1 f (v) ≠ 3 in some path in P 2 f(v)=0 v itself is a path in P 3 f(v)=1 v end vertex of some path in P n

f-path partition number pf(G) f-path-partition problem is to determine the f-path-partition number pf(G) which is the minimum cardinality of an f-path partition of G. p(G)=pf(G) when f(v)=2 for all vertices v in G.

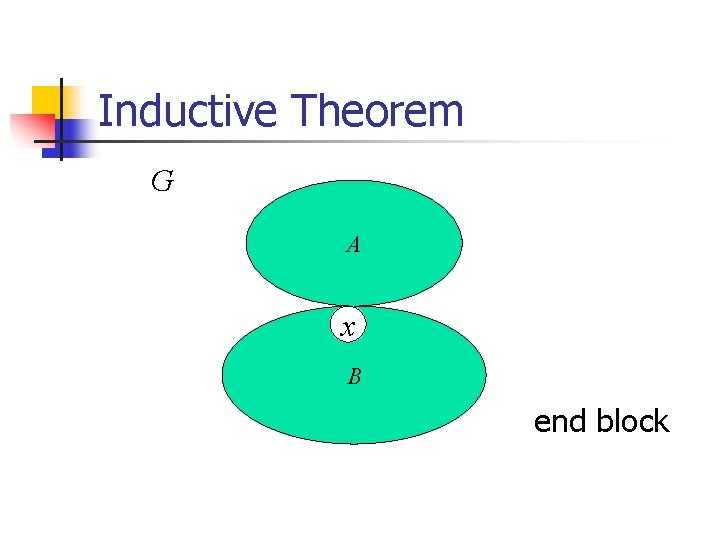
Inductive Theorem G A x B end block

Inductive Theorem x: a specified vertex of a graph H in which f is a vertex labeling. i=0, 1, 2, 3 f i : V(H) {0, 1, 2, 3} f i(y)=f(y) for all vertices y except f i(x)=i.

Inductive Theorem α=pf 0(B)-pf 1(B) β=pf 1(B)-pf 2(B) 1 f(x)=0 pf(G)=pf(A)+pf(B)-1. 2 f(x)=1 pf(G)=pf 1 -α(A)+pfα(B)-1.

Inductive Theorem 3 f(x) 2 and α=β=0 pf(G)=pf(A)+pf 0(B)-1. 4 f(x) 2 and α=0 and β=1 pf(G)=pf 3(A)+pf(B). 5 f(x) 2 and α=1 pf(G)=pf 1 -β (A)+pf 1+β(B)-1.

Basis Pf (B)=pf (B-f -1(0)) +|f -1(0)|. WLOG f -1(0)=Ø

Basis B: complete graph. f -1(1) ≠Ø or f -1(2)=Ø pf(B)= |f -1(1)|/2 else pf(B)=1.

Basis B is a path x: end vertex of B with f(x)=3 pf(B)=pf(B-x). x: end vertex of B with f(x)=2 pf(B)=pf 1(B). B: end vertex x and another vertex y with f(x)=f(y)=1 no vertex between x and y has a label 1 pf(B)=pf(B ’)+1 B’: path obtained from B by deleting [x, y].

Basis B is a cycle. f -1(2)=Ø pf(B)= |f -1(1)|/2. P: [x, y] in B such that f -1(1) ∩P ={x, y} and f -1(2) ∩P≠Ø pf(B)=pf(B-P)+1.

Basis B is a complete bipartite graph c 1=d 1=0 and c 2 d 2 and x C 2 pf(B)=pf '(B) f ' is the same as f except f '(x)=1. C C 1 C 2 C 3 D 1 D 2 D 3 D x f(x)=2 x f(x)=1

Basis x C 1. Also, either d 2 1 with y D 2, or else c 1>d 1 and d 2=0<d 3 with y D 3. Then pf(B)=pf '(B-x), where f' is the same as f except f'(y)=1. x f(x)=1 y f(y)=2 y f(y)=1

Our Result f-path partition: a collection of vertex-disjoint paths 0 a 1 b 2 c 3 d

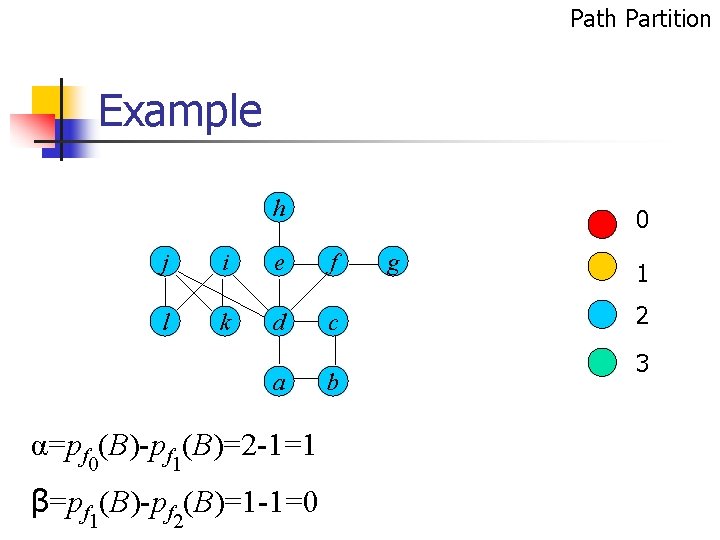
Path Partition Example h 0 j i e f l k d c a α=pf 0(B)-pf 1(B)=2 -1=1 β=pf 1(B)-pf 2(B)=1 -1=0 b g 1 2 3

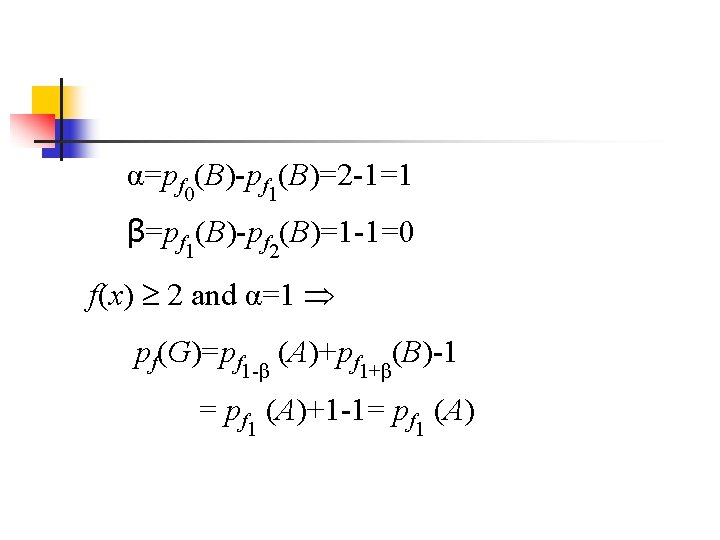
α=pf 0(B)-pf 1(B)=2 -1=1 β=pf 1(B)-pf 2(B)=1 -1=0 f(x) 2 and α=1 pf(G)=pf 1 -β (A)+pf 1+β(B)-1 = pf 1 (A)+1 -1= pf 1 (A)

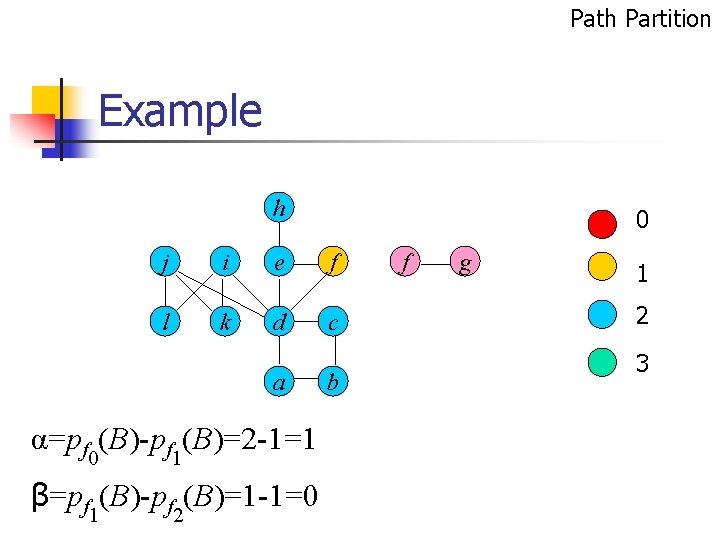
Path Partition Example h 0 j i e f l k d c a α=pf 0(B)-pf 1(B)=2 -1=1 β=pf 1(B)-pf 2(B)=1 -1=0 b f g 1 2 3

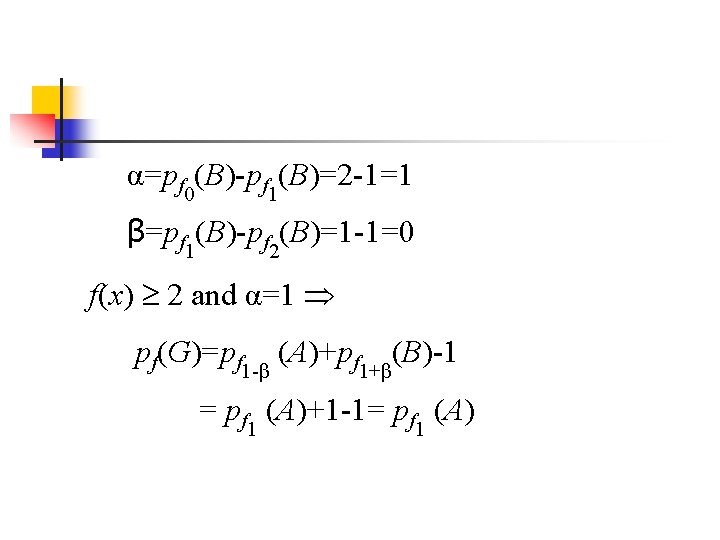
α=pf 0(B)-pf 1(B)=2 -1=1 β=pf 1(B)-pf 2(B)=1 -1=0 f(x) 2 and α=1 pf(G)=pf 1 -β (A)+pf 1+β(B)-1 = pf 1 (A)+1 -1= pf 1 (A)

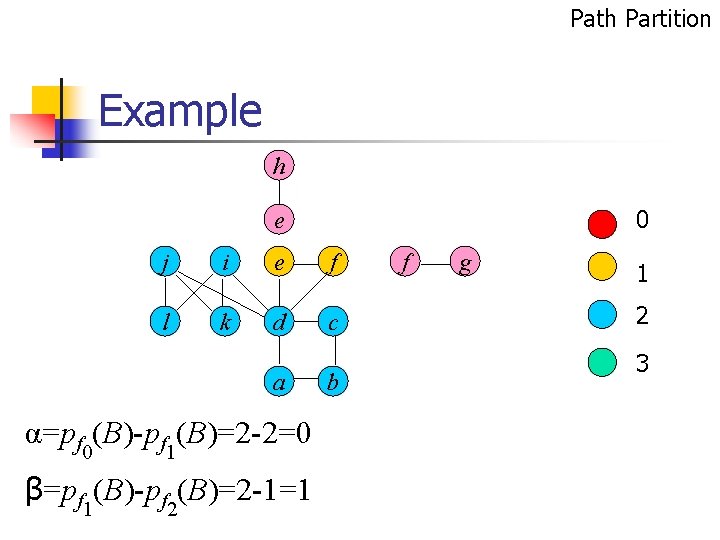
Path Partition Example h 0 e j i e f l k d c a α=pf 0(B)-pf 1(B)=2 -2=0 β=pf 1(B)-pf 2(B)=2 -1=1 b f g 1 2 3

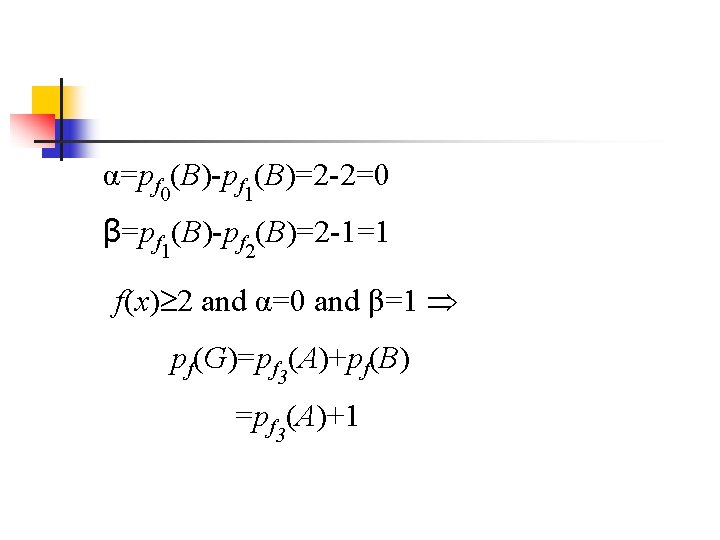
α=pf 0(B)-pf 1(B)=2 -2=0 β=pf 1(B)-pf 2(B)=2 -1=1 f(x) 2 and α=0 and β=1 pf(G)=pf 3(A)+pf(B) =pf 3(A)+1

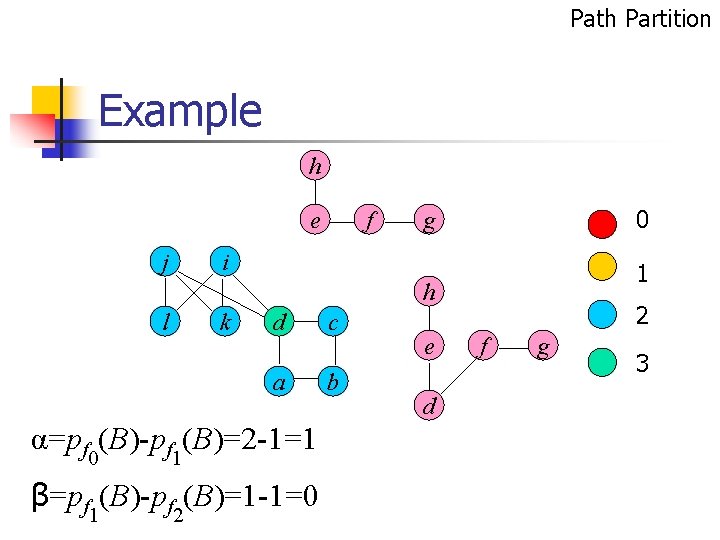
Path Partition Example h e j f 0 g i 1 h l k d a α=pf 0(B)-pf 1(B)=2 -1=1 β=pf 1(B)-pf 2(B)=1 -1=0 c b e d 2 f g 3

f(x) 2 and α=1 pf(G)=pf 1 -β (A)+pf 1+β(B)-1 = pf 1 (A)+1 -1= pf 1 (A)

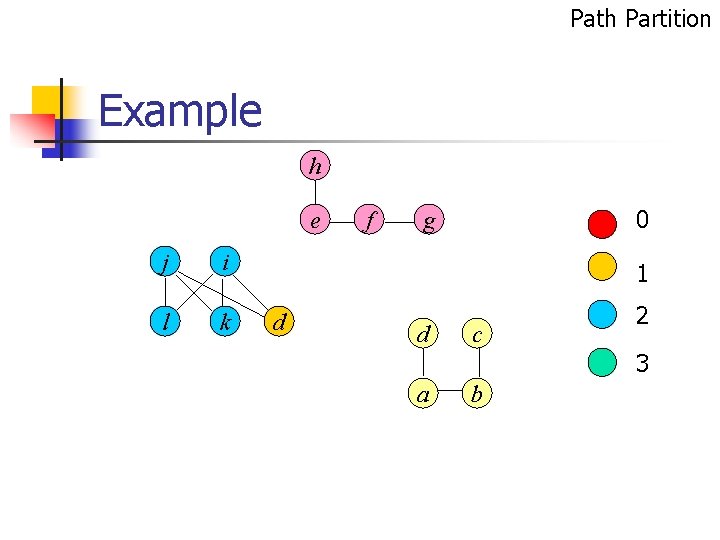
Path Partition Example h e j i l k f 0 g 1 d d c 2 3 a b

x C 1. d 2 1 with y D 2, Then pf(B)=pf'(B-x), where f' is the same as f except f'(y)=1.

Path Partition Example 0 j i 1 l k 2 3

Path Partition Example 0 j l 1 k 2 3

Path Partition Example 0 j 1 l 2 3

Path Partition Example 0 l j i l k 1 d a c b 2 3

Path Partition Example h j i e f l k d c a b g

Time Complexity n n The depth-first search to find all blocks and cut-vertices, and requires O(|E|) time Each subroutine requires O(|V(B)|+|E(B)|) operations.

Future work Path partition n Tree structure →small separator structure

Thanks for your attention