Path Integral Quantum Monte Carlo Consider a harmonic

Path Integral Quantum Monte Carlo • Consider a harmonic oscillator potential • a classical particle moves back and forth periodically in such a potential • x(t)= A cos( t) • the quantum wave function can be thought of as a fluctuation about the classical trajectory

Feynman Path Integral • The motion of a quantum wave function is determined by the Schrodinger equation • we can formulate a Huygen’s wavelet principle for the wave function of a free particle as follows: • each point on the wavefront emits a spherical wavelet that propagates forward in space and time

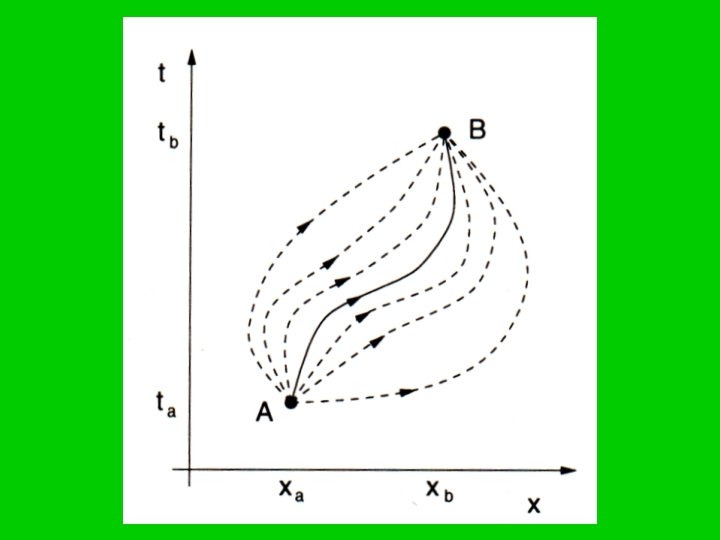
Feynman Paths • The probability amplitude for the particle to be at xb is the sum over all paths through spacetime originating at xa at time ta

Principal Of Least Action • Classical mechanics can be formulated using Newton’s equations of motion or in terms of the principal of least action • given two points in space-time, a classical particle chooses the path that minimizes the action Fermat

Path Integral • L is the Lagrangian L=T-V • similarly, quantum mechanics can be formulated in terms of the Schrodinger equation or in terms of the action • the real time propagator can be expresssed as

Propagator • The sum is over all paths between (x 0, 0) and (x, t) and not just the path that minimizes the classical action • the presence of the factor i leads to interference effects • the propagator G(x, x 0, t) is interpreted as the probability amplitude for a particle to be at x at time t given it was at x 0 at time zero

Path Integral • We can express G as • Using imaginary time =it/

Path Integrals • Consider the ground state • as • hence we need to compute G and hence S to obtain properties of the ground state

Lagrangian • Using imaginary time =it the Lagrangian for a particle of unit mass is • divide the imaginary time interval into N equal steps of size and write E as

Action • Where j = j and xj is the displacement at time j

Propagator • The propagator can be expressed as

Path Integrals • • This is a multidimensional integral the sequence x 0, x 1, …, x. N is a possible path the integral is a sum over all paths for the ground state, we want G(x 0, N ) and so we choose x. N = x 0 • we can relabel the x’s and sum j from 1 to N

Path Integral • We have converted a quantum mechanical problem for a single particle into a statistical mechanical problem for N “atoms” on a ring connected by nearest neighbour springs with spring constant 1/( )2

Thermodynamics • This expression is similar to a partition function Z in statistical mechanics • the probability factor e- E in statistical mechanics is the analogue of e- E in quantum mechanics • =N plays the role of inverse temperature =1/k. T

Simulation • We can use the Metropolis algorithm to simulate the motion of N “atoms” on a ring • these are not real particles but are effective particles in our analysis • possible algorithm: • 1. Choose N and such that N >>1 ( low T) also choose ( the maximum trial change in the displacement of an atom) and mcs (the number of steps)

Algorithm • 2. Choose an initial configuration for the displacements xj which is close to the approximate shape of the ground state probability amplitude • 3. Choose an atom j at random and a trial displacement xtrial ->xj +(2 r-1) where r is a random number on [0, 1] • 4. Compute the change E in the energy

Algorithm • If E <0, accept the change • otherwise compute p=e- E and a random number r in [0, 1] • if r < p then accept the move • if r > p reject the move

Algorithm • 4. Update the probability density P(x). This probability density records how often a particular value of x is visited Let P(x=xj) => P(x=xj)+1 where x was position chosen in step 3 (either old or new) • 5. Repeat steps 3 and 4 until a sufficient number of Monte Carlo steps have been performed qmc 1

Excited States • To get the ground state we took the limit • this corresponds to T=0 in the analogous statistical mechanics problem • for finite T, excited states also contribute to the path integrals • the paths through spacetime fluctuate about the classical trajectory • this is a consequence of the Metropolis algorithm occasionally going up hill in its search for a new path