PATH CONSISTENCY FOR 1 GENERAL CSPS 2 STPS

PATH CONSISTENCY FOR 1 - GENERAL CSPS 2 - STPS Peter Schlette Wesley Botham CSCE 990 Advanced CP, Fall 2009

Outline 2 General CSPs Review of Path Consistency & PC Algorithms Path Consistency Algorithms PC-1, PC-2, DPC, PC-8, PC-2001 STPs Review of Triangulated Graphs Path Consistency on STPs Floyd-Warshall, Bellman-Ford, STP, P 3 C, Prop-STP 9/26/2020

Path Consistency: Properties 3 A CSP is path consistent iff it is strongly 3 -consistent [van Beek & Dechter, JACM 95] PC algorithms typically iterate over triplets of variables Domains are filtered by arc consistency Consistent solutions over 2 variables can be extended to every 3 rd variable End variables in triplets need not be distinct In STP, variables domains are not relevant, thus PC algorithms on STPs enforce only 3 -consistency A given algorithm Must determine that a CSP is path consistent or not May or may not filter the constraints as much as possible (e. g. , DPC) 9/26/2020

List of Algorithms Discussed 4 PC-1 PC-2 DPC PC-8 PC-2001 [Mackworth 77, , Dechter Fig 3. 10] [Mackworth 77, Dechter Fig 3. 11] [Dechter & Pearl 89, Dechter Fig. 4. 9] [Bliek & Sam-Haroud 99] [Chmeiss & Jégou 98] [Bessière et al. 05] 9/26/2020

Path Consistency: Algorithms 5 They all stop when a relation/domain is empty; omitted for clarity Queue Does is it have one? Edges (e. g. , PPC) Triplets of variables (e. g. , PC-2) Tuples of ‘vv-pair, variable’ (e. g. , PC-8 & PC-2001) Properties Determines strong 3 -consistency? What is the time and space complexity? Requires additional data structures to remember supports? Graph: Complete? Chordal? What is the practical performance (i. e. , phase transition)? 9/26/2020

PC-1 [Mackworth 77] 6 1 Repeat until quiescence 2 For i, j, k variables 3 Rij Rik Rkj Has 4 nested loops, iterates over vertices, needs no queue Updates every edge & every domain (i=j) Uses composition and intersection Determines strong 3 -consistency (when i=j) Time complexity is O(n 5 d 5) One sweep costs O(n 3 d 3) Number of sweeps O(n 2 d 2) Space: no queue, no additional data structure, complete graph 9/26/2020

PC-2 [Mackworth 77] 7 k 1 Q { (i, j, k) | i j, i k, j k } i j 2 While Q is not empty 3 For (i, j, k) from Q m m 4 Rij Rik Rjk 5 If Rij changed, Q Q U { (m, i, j), (m, j, i) | m i, m j } Has 1 loop over a queue of triplets of variables When an edge (domain) is updated, only triplets with an ‘external’ 3 rd node are added to queue Allows i=j, thus determines strong 3 -consistency. Dechter Fig 3. 11 specifies i<j in which case domains are not updated Theoretically & practically faster than PC-1 (queue) Time complexity is O(n 3 d 5) Space: Queue size is O(n 3), no additional data structures, complete graph 9/26/2020

PC-1 vs. PC-2 [Botham & Schlette] 8 n=16, a=16, d=30% PC-1 PC-2 9/26/2020

PPC [Bliek & Sam-Haroud 99] 9 Q ← E Until Q is empty do edge ← DEQUEUE(Q) for every triplet i, j, k related to edge Rij ← Rij ∩ (Rik Rkj) if Rij was changed then En. Queue((i, j), Q) First triangulates the graph Keeps Q, a queue of edges For an edge in Q Pops edge from Q, retrieves all triplets where edge appears In each triplet, updates each edge Each updated edge is added to Q Does not specify whether or not domains are filtered (some should be for soundness) 9/26/2020

PPC [Bliek & Sam-Haroud 99] 10 Triangulated graph is usually sparser than complete graph For triplet (i, j, k) allows i=j, algorithm is sound (not clear in paper) j Enforces Strong path-consistency Weaker filtering than PC-2 v 1 i Time: O( ed 2), degree of graph v 2 vn Space: queue O( e) for storing triplets, no additional data structure, chordal graph Weakness: if 2 or more edges of a given triplet are in Q All three edges are updated once for each edge May do redundant work (fixed in STP) 9/26/2020

DPC [Dechter Fig 4. 9, Dechter & Pearl 89] 11 1 For k=n downto 1 do 2 For i =1 to k REVISE(i, Rik) 3 For i, j k i, k connected & j, k connected 4 Rij Rik Rjk k-6 k-4 k-2 k Given an ordering for the variables From bottom to top, enforces directional arc-consistency (DAC) From bottom to top, for every variable, updates the edge between every two of its parents Properties Moralizes the graph, determines strong directional path consistency relative to ordering Time O(min(t. d 3, n 3 d 3)) Space: No queue, no additional data structures, chordal graph 9/26/2020

DPC: Constraint revision [Dechter Fig 3. 9] 12 1 For each (a, b) Rij 2 If no c Dk is s. t. (a, c) Rik & (a, b) Rjk 3 Remove (a, b) from Rij i j k Does not operate on matrices in reality ( , ) Iterates over Tuples in constraints (i. e. , (a, b) Rij) and Values in domain (i. e. , c Dk) Not yet tested against PC-1, PC-2, PPC 9/26/2020

PC-8 [Chmeiss & Jégou 98] 13 PC-8 INITIALIZE While Q do POP((i, a), k), Q) PROPAGATE((i, a), k) INITIALIZE Q ← for i, j, k=1 to n (i<j, k≠i, k≠j) for (a, b) Rij UPDATE((i, a), (j, b), k) UPDATE if WITHOUTSUPPORT((i, a), (j, b), k) REMOVE (a, b) from Rij, (b, a) from Rij Q ← Q U {((i, a, )j), ((j, b), i)} PROPAGATE for j=1 to n (j≠i, j≠k) for b Dj and (a, b) Rij UPDATE((i, a), (j, b), k) 9/26/2020

PC-8 Analysis [Chmeiss & Jégou 98] 14 Queue: a list of (vvp, var) = ((var, val), var) Determines strong PC-property (if you allow i=j) Achieves ‘full’ filtering Time complexity INITIALIZATION: O(n 3 d 3) PROPAGATE is called O(n 2 d 2) times, each call costs O(nd 2) PC-8: INITIALIZATION + (n 2 d 2) PROPAGATE = O(n 3 d 4) Space 9/26/2020

PC-8 vs. PC-2 [Botham & Schlette] 15 n=16, a=16, d=30% PC-2 PC-8 9/26/2020

PC-2001 [Bessière+ 05] 16 PC-2001 1 INITIALIZE(Q) 2 While Q 3 POP((i, a), k) from Q 4 REVISEPATH((i, a), j) INITIALIZE(Q) 1 For i, j, k variables 2 For each (a, b) Rij 3 If (a, b) has no support c in Dk 4 Remove (a, b) from Rij 5 Q Q U {((i, a), j), ((j, b), i)} 6 Else 7 Last((i, a), (j, b), k) the first support of (a, b) Dk 9/26/2020

PC-2001 [Bessière+ 05] 17 REVISEPATH((i, a), k, Q) 1 For each j k 2 For each b Dj | (a, b) Rij 3 support Last((i, a), (j, b), k) 4 While support is nil or was deleted 5 support next value in Dk 6 If no supports exist 7 Remove (a, b) from Rij 8 Q Q U {((i, a), j), ((j, b), i)} 9 Else 10 Last((i, a), (j, b), k) support Records supporting values to improve time complexity (at the cost of space overhead) 9/26/2020

PC-2001 Analysis [Bessière+ 05] 18 Queue: same as PC-8, list of (vvp, var) Achieves the same properties as PC-1, PC-2, PC-8 Time: O(n 3 d 3) Space Queue: O(n 2 d) Data structure: Last structure dominates O(n 3 d 2) Graph complete Compared to PC-8, PC-2001 Is easier to understand implement Has lower time complexity Is faster in general in experiments Has worse space complexity 9/26/2020

PC-2001 vs. PC-2, PC-8 [Botham & Schlette] 19 n=16, a=16, d=30% PC-2 PC-8 PC-2001 9/26/2020

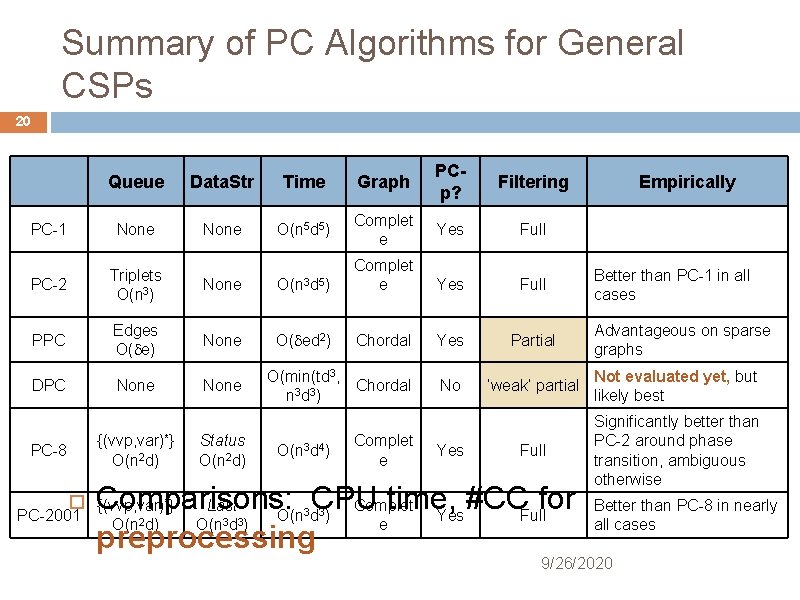
Summary of PC Algorithms for General CSPs 20 Queue Data. Str Time Graph PCp? Filtering PC-1 None O(n 5 d 5) Complet e Yes Full PC-2 Triplets O(n 3) None O(n 3 d 5) Complet e Yes Full PPC Edges O( e) None O( ed 2) Chordal Yes Partial DPC None O(min(td 3, Chordal n 3 d 3 ) No ‘weak’ partial Not evaluated yet, but likely best Full Significantly better than PC-2 around phase transition, ambiguous otherwise PC-8 {(vvp, var)*} O(n 2 d) Status O(n 2 d) O(n 3 d 4) Complet e Yes Empirically Better than PC-1 in all cases Advantageous on sparse graphs Comparisons: CPU time, #CC for Last Complet Better than PC-8 in nearly O(n d ) Yes Full O(n d) O(n d ) e all cases preprocessing {(vvp, var)*} PC-2001 2 3 3 9/26/2020

Outline 21 General CSPs Review of Path Consistency & PC Algorithms Path Consistency Algorithms PC-1, PC-2, DPC, PC-8, PC-2001 STPs Review of Triangulated Graphs Path Consistency on STPs Floyd-Warshall, Bellman-Ford, STP, P 3 C, Prop-STP 9/26/2020

Triangulated Graphs: Motivation 22 [Bliek & Sam-Haroud 99] showed that PPC Operates on triangulated graphs Determines the property of strong path consistency When constraints are convex, PPC also yields minimal CSP [Xu & Choueiry 03] studied STP In STP constraints are convex Proposed STP, which adapts PPC to STPs w/o updating domains (‘weak’ path consistency) May do fewer updates than PPC: queue of edges versus queue of triangles [Planken et al. 08] studied STP Showed that STP is O(t 2), t is the number of triangles Proposed P 3 C, for STP, that is O(t) 9/26/2020

Vertex elimination 23 Vertex elimination operation: When removing a vertex, connect all neighbors if they are not already connected Fill edges: are the edges added when eliminating a vertex Simplicial vertex Vertex whose neighbors are all connected (form a clique) Eliminating a simplicial vertex does not add any edges Perfect elimination ordering: There is always a simplicial vertex to be eliminated. All nodes can be eliminated w/o adding any fill edges 9/26/2020

Triangulated Graphs 24 A graph is triangulated iff it has a perfect elimination order The width of the triangulated graph is equal to the size of its largest clique -1. Why? Finding the width is tractable, thus max. clique on triangulated graph is tractable (usually, NP-hard) Using the reverse of the perfect elimination ordering of a triangulated graph yields A moralized graph The induced width of this ordering is equal to the width of the triangulated graph, why? Moralizing an arbitrary ordering of a graph yields a triangulated graph. Why? 9/26/2020

Outline 25 General CSPs Review of Path Consistency & PC Algorithms Path Consistency Algorithms PC-1, PC-2, DPC, PC-8, PC-2001 STPs Review of Triangulated Graphs Path Consistency on STPs Floyd-Warshall, Bellman-Ford, STP, Prop-STP, P 3 C (Prop-STP is not discussed for lack of time) 9/26/2020

Floyd-Warshall for STP [CLR] 26 FLOYDWARSHALL For k 1 to n For i 1 to n For j 1 to n w(eij) MIN(w(eij), w(eik)+w(ekj)) Basic STP solver, three nested loops Initialization: builds the distance graph Rij = [a, b] gives eij b and eji -a When edge does not exist, add infinite distance (complete graph) Time (n 3), Space: No queue but O(n 2) new edges 9/26/2020

Bellman-Ford for STP 27 [CLR] d[s] 0 for each vertex i other than source (i s) d[i] Repeat n-1 times for each edge eij if d[i] + w(eij) < d[j] then d[j] d[i] + w(eij) for each edge eij if d[i] + w(eij) < d[j] then return inconsistent Time: O(en), Space: No queue but O(n) new edges Detects path consistency Edges are not guaranteed minimal 9/26/2020

∆STP [Xu & Choueiry 03] 28 PPC Operates on triangulated graphs ‘Fully’ filters convex constraints ∆STP adapts & refines PPC to STP Keeps a queue of triangles (vs. a queue of edges) Pops a triangle from queue & updates all 3 edges Implicitly separate graph in biconnected components Enqueues triangles adjacent to only the updated edge 9/26/2020 Best performance when queue is FIFO

Performance on STPs: F-W, PPC, STP [Xu & Choueiry 03] 29 9/26/2020

Performance on STPs: BF, DPC, STP [Shi+ 05] 30 9/26/2020

3 P C: The Idea [Planken+ 08] 31 Designers of ∆STP became aware of relevance of simplicial ordering in ∆STP in 2005 (ref. Nic Wilson) Designers of Prop-STP exploited the idea The authors of P 3 C formalize the flaw of ∆STP Identified a pathological case where ∆STP does unnecessary work (not useful filtering) Characterized it as set of problems where ∆STP runs in Ω(t 2), where t is the number of triangles P 3 C addresses flaw by using a simplicial ordering Proves that propagation can be achieved in (t) 9/26/2020

P 3 C: Pathological Case [Planken+ 08] 32 {ci→i+1 | 0 ≤ i ≤ t+1} with zero weight {ci→j | (1 ≤ i ≤ j− 2 < t) ∧ i+j−t ∈ {1, 2}} with weight j−i− 1 {cj→i | (1 ≤ i ≤ j− 2 < t) ∧ i+j−t ∈ {1, 2}} with weight t−(j−i− 1) 9/26/2020

Path. Case: Empirically 08] cu bic 33 [Planken+ c ati r ad u q linear 9/26/2020

3 P C: The Algorithm [Planken+ 08] 34 Given: A triangulated graph & a perfect elimination order The algorithm has two steps i Bottom up: For every node j Considers every pair of parents Updates the edge between parents (ref. DPC) Top down: For every node Considers every pair of parents Updates edges adjacent to node i 1 j 2 k 9/26/2020 k

3 P C: Bottom up [Planken+ 08] 35 DPC: For each node update the edges between all parents given the edges with the node 9/26/2020

3 P C: Top Down [Planken+ 08] 36 Update the edges between every node and its parent 9/26/2020

P 3 C: Sound & complete 37 [Planken+ 08] Claim: on iteration k of P 3 C’s second half, all edges in the subgraph consisting of { Vi | i ≤ k } are minimal Base case: k = 2 We know that c 1, 2 (in orange) must be minimal if it exists, due to DPC; the subgraph will always be minimal for k = 2 1 k=2 1 2 k=3 9/26/2020

P 3 C: Sound & complete 38 [Planken+ 08] Induction hypothesis: Gk-1={Vi≤k-1} forms a minimal subgraph Induction step: Gk-1 minimal Gk minimal In the kth iteration, wik=min(wik, wij+ wjk) Any part of a theoretical shorter path that extends out of the Gk-1 can be replaced by its two endpoints within Gk-1, due to the filtering from DPC The only way wik could be non-minimal is if there were a shorter path wij+wjk, but this path was checked in the kth iteration We have a base step and an inductive 9/26/2020 step, so the proof is complete! 1 Gk-1 Gk i j k-1 k

Time Complexity [Planken+ 08] 39 P 3 C runs in Θ(t), t is the number of triangles O(t) ⊆ O(n w*2), w* is the min. induced width O(n w*2) ⊆ O(nδ 2), where δ is max. degree O(nδ 2) ⊆ O(n 3) DPC visits each triangle exactly once The second half of P 3 C visits each triangle exactly once Thus we have a constant number of visits to each triangle and a linear time complexity in the number of triangles 9/26/2020

Jobshop (enforced consistency) [Planken+ 08] 40 In spite of theoretical bounds, the two algorithms are quite close 9/26/2020

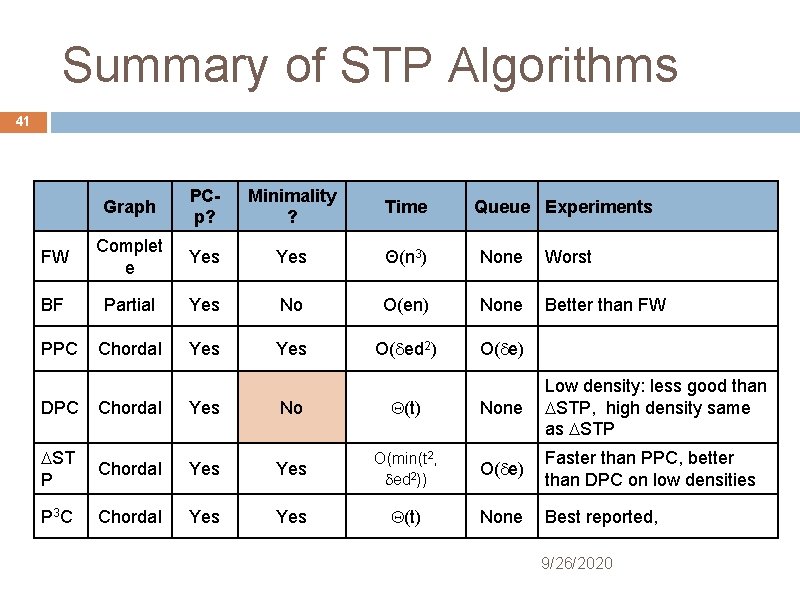
Summary of STP Algorithms 41 Graph PCp? Minimality ? Time FW Complet e Yes Θ(n 3) None Worst BF Partial Yes No O(en) None Better than FW Chordal Yes O( ed 2) O( e) PPC DPC Chordal Yes Queue Experiments No (t) None Low density: less good than STP, high density same as STP O( e) Faster than PPC, better than DPC on low densities None Best reported, ST P Chordal Yes O(min(t 2, ed 2)) P 3 C Chordal Yes (t) 9/26/2020

Future Work [Planken+ 08] 42 Extend P 3 C to general CSPs Investigate efficiency of triangulation algorithms vs. P 3 C Incremental P 3 C solver for STPs 9/26/2020

References 43 CSP PC-1, PC-2: see [Mackworth, AIJ 1977] PPC: see [Bliek & Sam-Haroud, IJCAI 1999] DPC: see [Dechter 4. 2. 2, Dechter & Pearl, AIJ 1987] PC-8: see [Chmeiss & Jégou, IJAITools 1998] PC-2001: see [Bessière et. Al, AIJ 2005] STP Floyd-Warshall, Bellman-Ford: see CLR textbook DPC: see [Dechter et al. , AIJ 1991] ∆STP: see [Xu and Choueiry, TIME 2003] Prop-STP: see [Bui, Tyson, and Yorke-Smith, AAAI 07, Workshop] 9/26/2020 P 3 C: see [Planken et al. , ICAPS 2008]