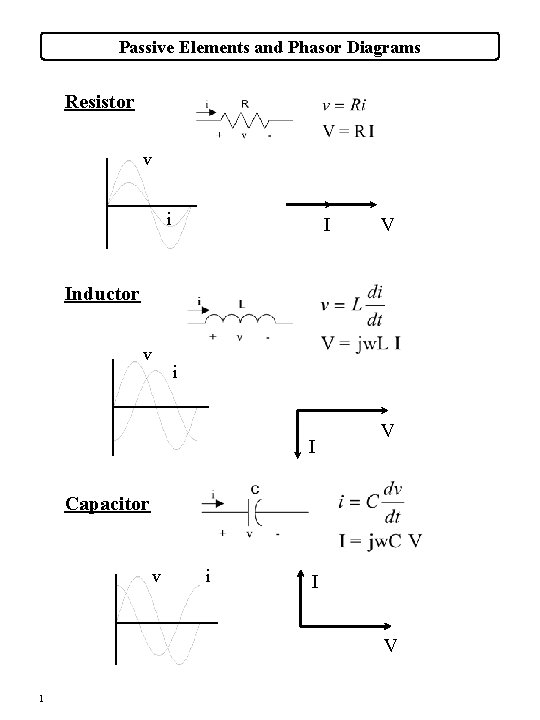
Passive Elements and Phasor Diagrams Resistor v i

Passive Elements and Phasor Diagrams Resistor v i I V Inductor v i I V Capacitor v i I V 1

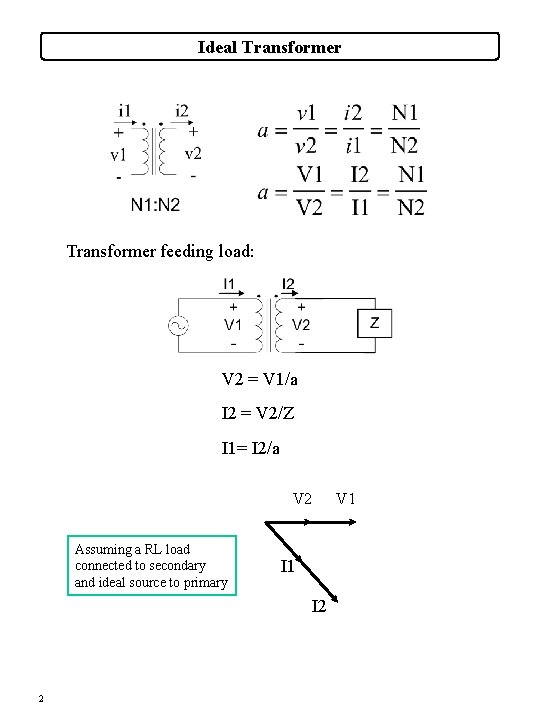
Ideal Transformer feeding load: V 2 = V 1/a I 2 = V 2/Z I 1= I 2/a V 2 Assuming a RL load connected to secondary and ideal source to primary I 1 I 2 2 V 1

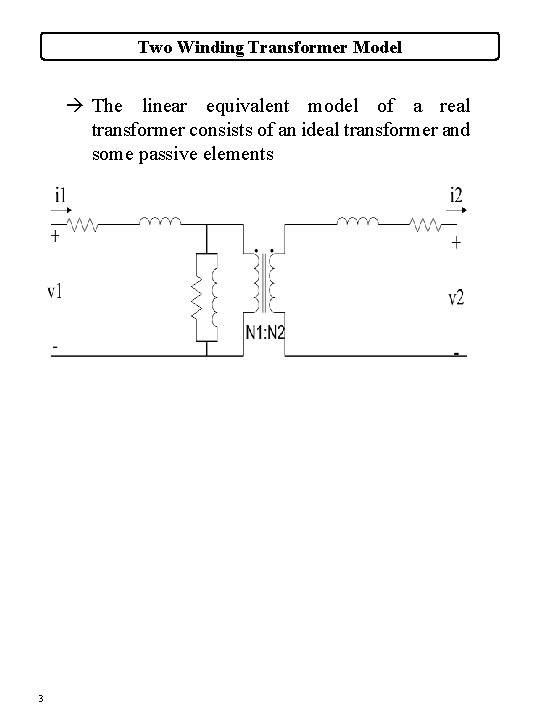
Two Winding Transformer Model à The linear equivalent model of a real transformer consists of an ideal transformer and some passive elements 3

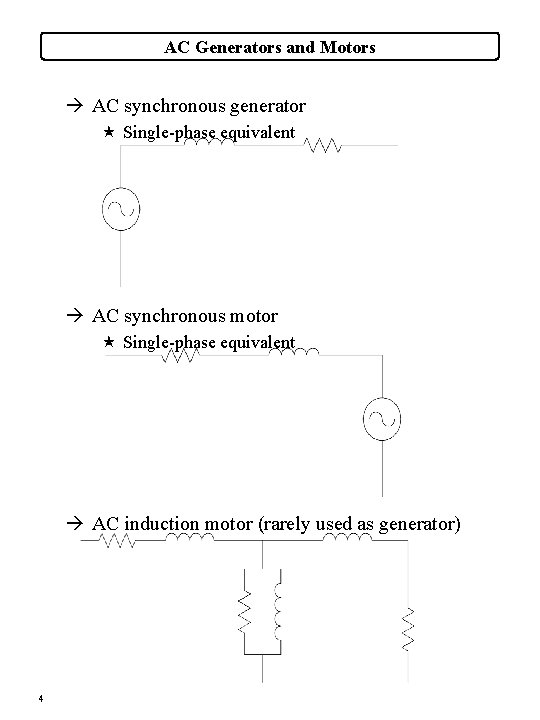
AC Generators and Motors à AC synchronous generator « Single-phase equivalent à AC synchronous motor « Single-phase equivalent à AC induction motor (rarely used as generator) 4

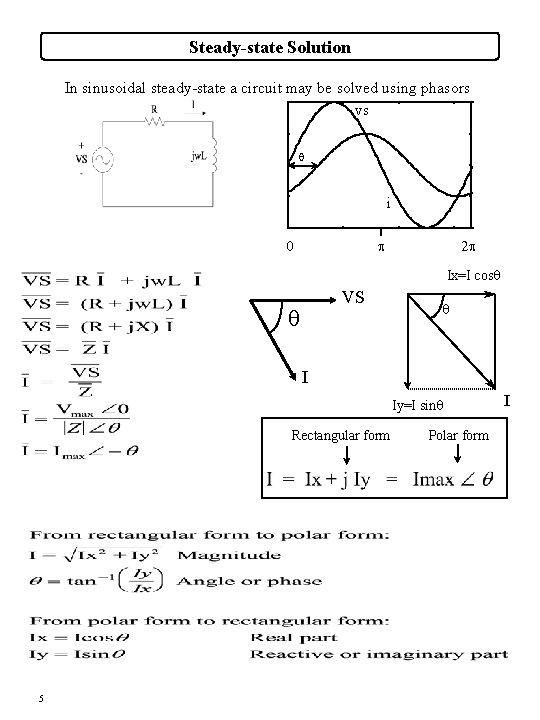
Steady-state Solution In sinusoidal steady-state a circuit may be solved using phasors vs q i 0 p 2 p Ix=I cosq VS q q I Iy=I sinq Rectangular form 5 Polar form I

Single-phase Power Definitions 6

Power Triangle S Ssin q=Q q P=Scosq 7 Real Power P = S cos q = V I cos q watts Reactive Power Q = S sin q = V I sin q vars

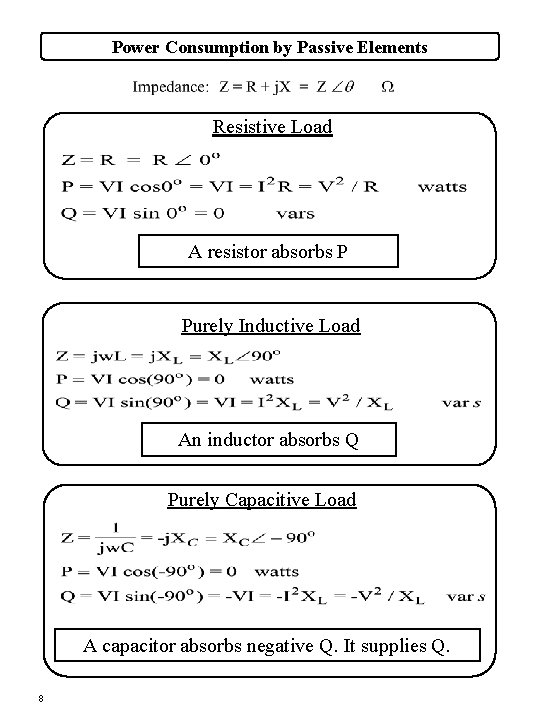
Power Consumption by Passive Elements Resistive Load A resistor absorbs P Purely Inductive Load An inductor absorbs Q Purely Capacitive Load A capacitor absorbs negative Q. It supplies Q. 8

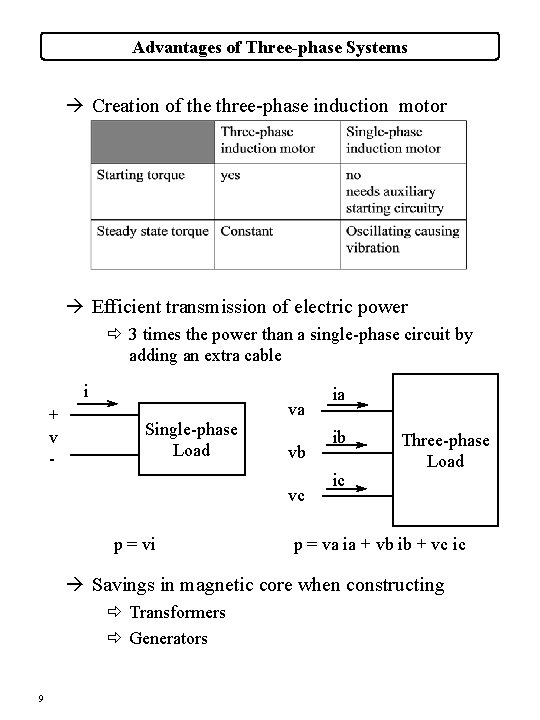
Advantages of Three-phase Systems à Creation of the three-phase induction motor à Efficient transmission of electric power ð 3 times the power than a single-phase circuit by adding an extra cable i + v - Single-phase Load va vb vc p = vi ia ib ic Three-phase Load p = va ia + vb ib + vc ic à Savings in magnetic core when constructing ð Transformers ð Generators 9

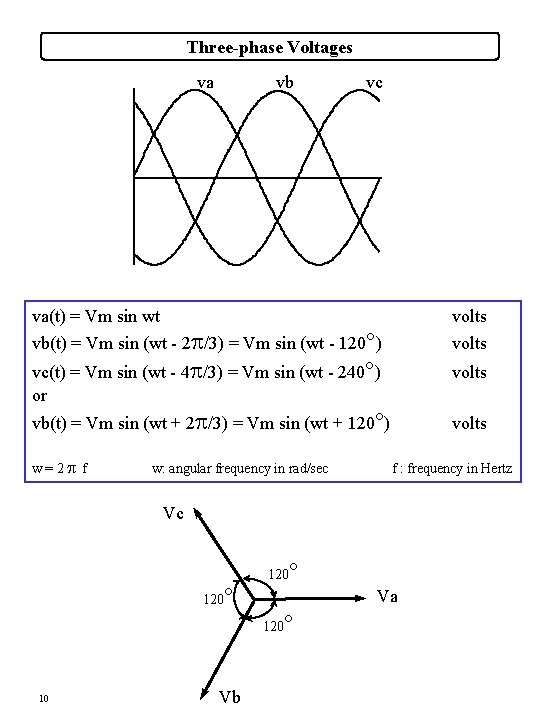
Three-phase Voltages va vb vc va(t) = Vm sin wt volts vb(t) = Vm sin (wt - 2 p/3) = Vm sin (wt - 120°) volts vc(t) = Vm sin (wt - 4 p/3) = Vm sin (wt - 240°) or volts vb(t) = Vm sin (wt + 2 p/3) = Vm sin (wt + 120°) w=2 pf w: angular frequency in rad/sec volts f : frequency in Hertz Vc ° 120 Va ° 120 10 Vb

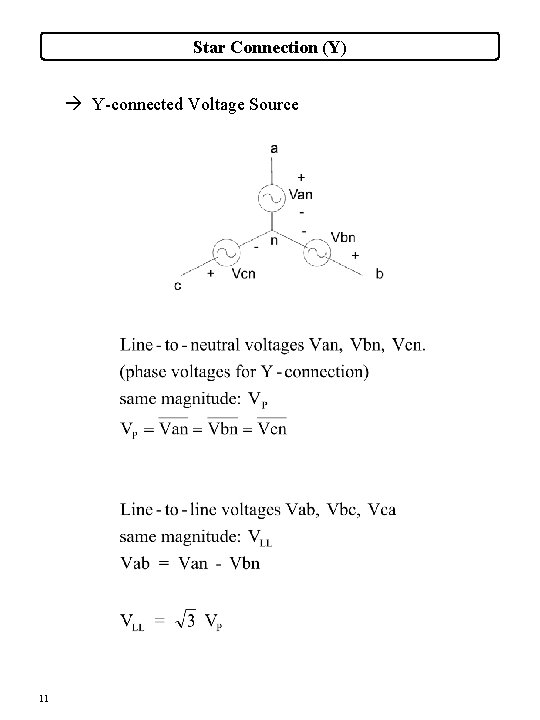
Star Connection (Y) à Y-connected Voltage Source 11

Delta Connection (D ) à D-connected Voltage Source 12

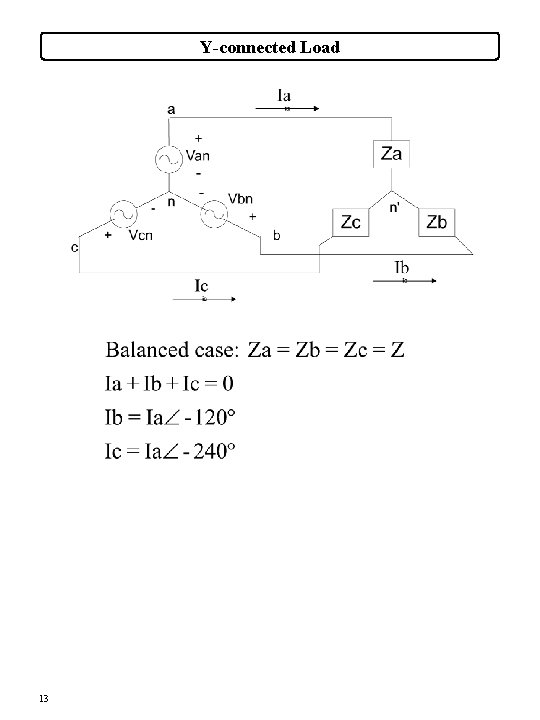
Y-connected Load 13

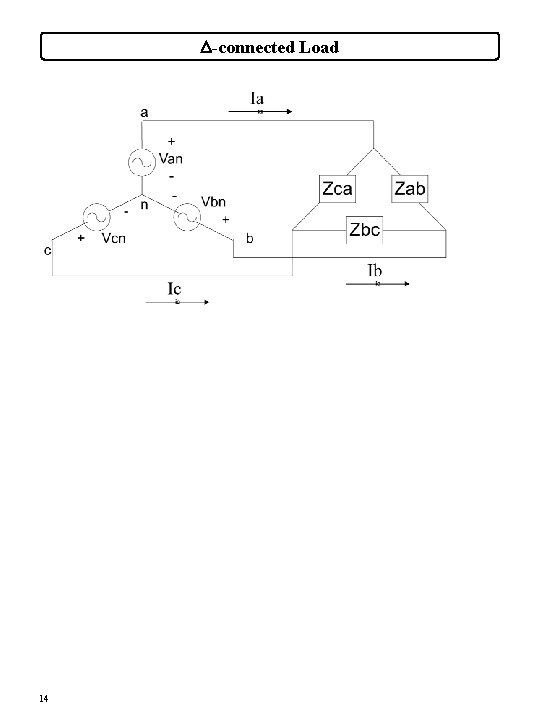
D-connected Load 14

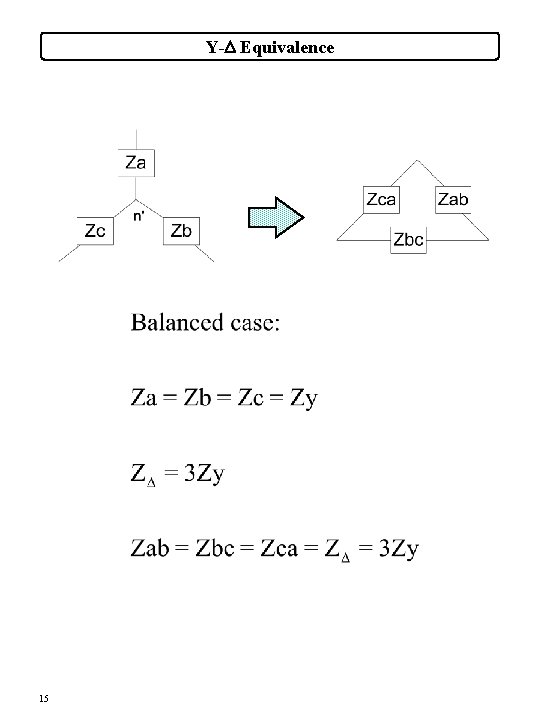
Y-D Equivalence 15

Power in Three-phase Circuits 16

Three-phase Power 17

Three-phase Transformers à Use of one three-phase transformer unit à Use of 3 single phase transformers to form a “Transformer Bank 18

Physical Overview 19

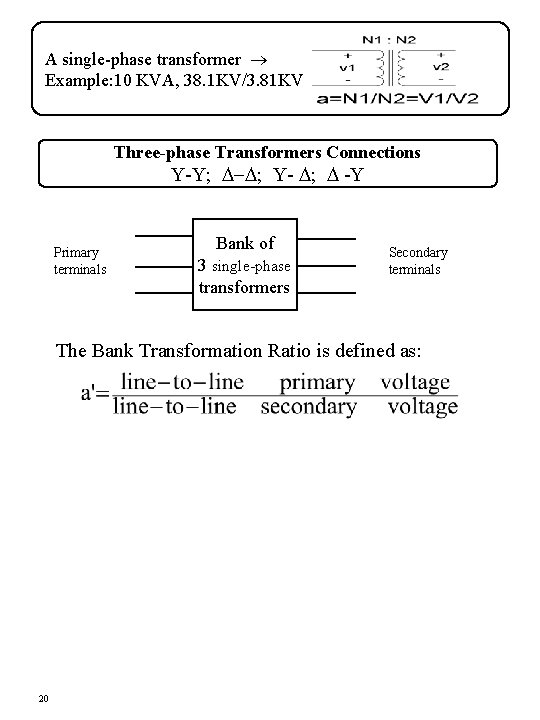
A single-phase transformer ® Example: 10 KVA, 38. 1 KV/3. 81 KV Three-phase Transformers Connections Y-Y; D-D; Y- D; D -Y Primary terminals Bank of 3 single-phase transformers Secondary terminals The Bank Transformation Ratio is defined as: 20

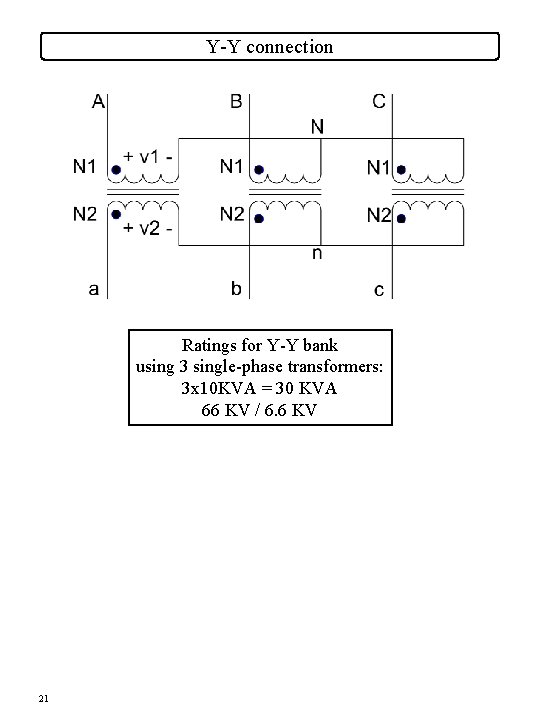
Y-Y connection Ratings for Y-Y bank using 3 single-phase transformers: 3 x 10 KVA = 30 KVA 66 KV / 6. 6 KV 21

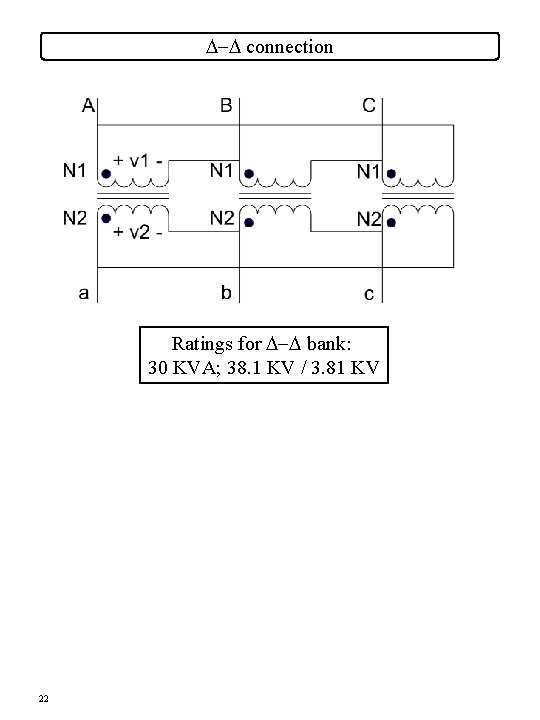
D-D connection Ratings for D-D bank: 30 KVA; 38. 1 KV / 3. 81 KV 22

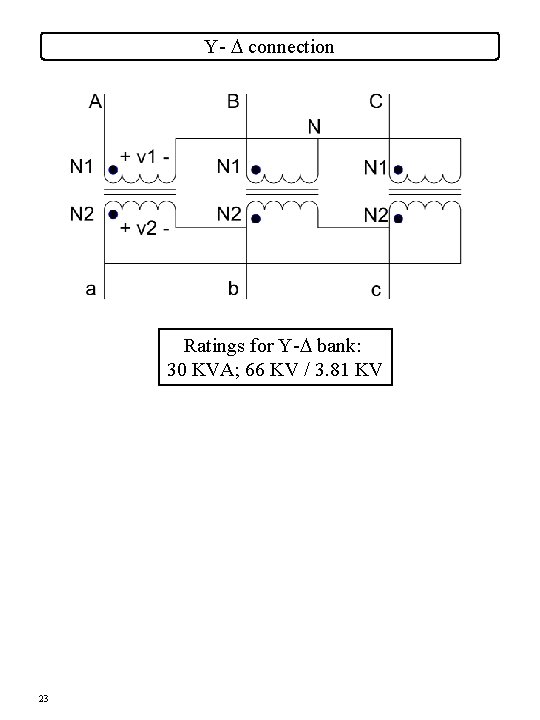
Y- D connection Ratings for Y-D bank: 30 KVA; 66 KV / 3. 81 KV 23

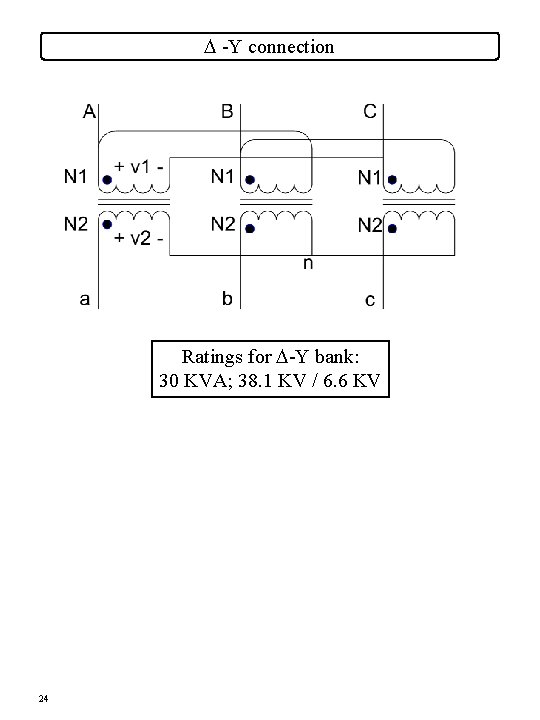
D -Y connection Ratings for D-Y bank: 30 KVA; 38. 1 KV / 6. 6 KV 24

Per unit modelling àPower lines operate at kilovolts (KV) and kilowatts (KW) or megawatts (MW) To represent a voltage as a percent of a reference value, we first define this BASE VALUE. Example: Base voltage: Vbase = 120 KV ** The percent value and the per unit value help the analyzer visualize how close the operating conditions are to their nominal values. 25

Defining bases 4 quantities are needed to model a network in per unit system: V: I: S: Z: voltage current power impedance VBASE IBASE SBASE ZBASE Given two bases, the other two quantities are easily determined. 26

Three phase bases In three-phase systems it is common to have data for the three-phase power and the line-to-line voltage. With p. u. calculations, three-phase values of voltage, current and power can be used without undue anxiety about the result being a factor of Ö 3 incorrect !!! 27

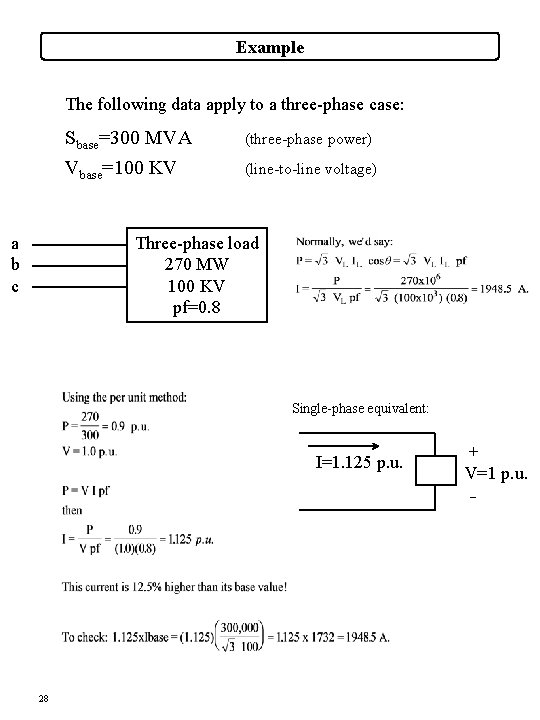
Example The following data apply to a three-phase case: a b c Sbase=300 MVA (three-phase power) Vbase=100 KV (line-to-line voltage) Three-phase load 270 MW 100 KV pf=0. 8 Single-phase equivalent: I=1. 125 p. u. + V=1 p. u. - 28

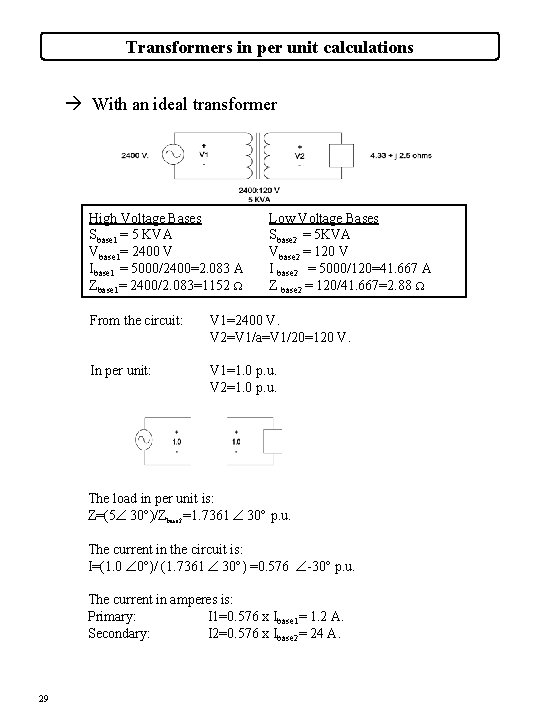
Transformers in per unit calculations à With an ideal transformer High Voltage Bases Sbase 1 = 5 KVA Vbase 1= 2400 V Ibase 1 = 5000/2400=2. 083 A Zbase 1= 2400/2. 083=1152 W Low Voltage Bases Sbase 2 = 5 KVA Vbase 2 = 120 V I base 2 = 5000/120=41. 667 A Z base 2 = 120/41. 667=2. 88 W From the circuit: V 1=2400 V. V 2=V 1/a=V 1/20=120 V. In per unit: V 1=1. 0 p. u. V 2=1. 0 p. u. The load in per unit is: Z=(5Ð 30°)/Zbase 2 =1. 7361 Ð 30° p. u. The current in the circuit is: I=(1. 0 Ð 0°)/ (1. 7361 Ð 30°) =0. 576 Ð-30° p. u. The current in amperes is: Primary: I 1=0. 576 x Ibase 1= 1. 2 A. Secondary: I 2=0. 576 x Ibase 2= 24 A. 29

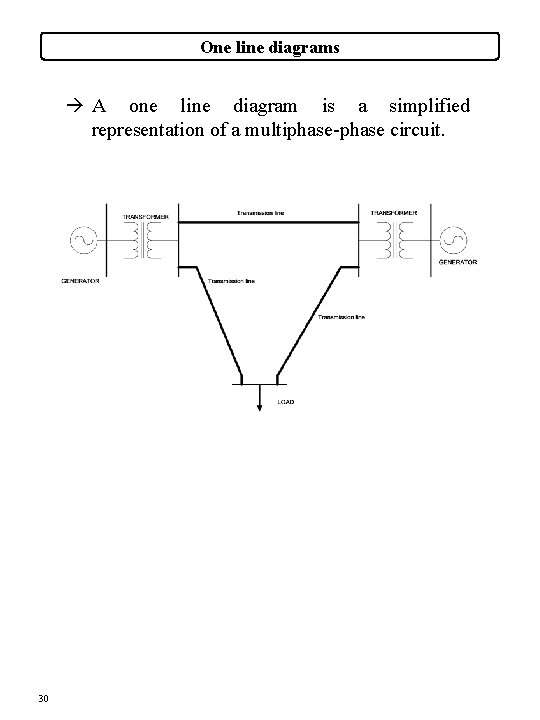
One line diagrams à A one line diagram is a simplified representation of a multiphase-phase circuit. 30

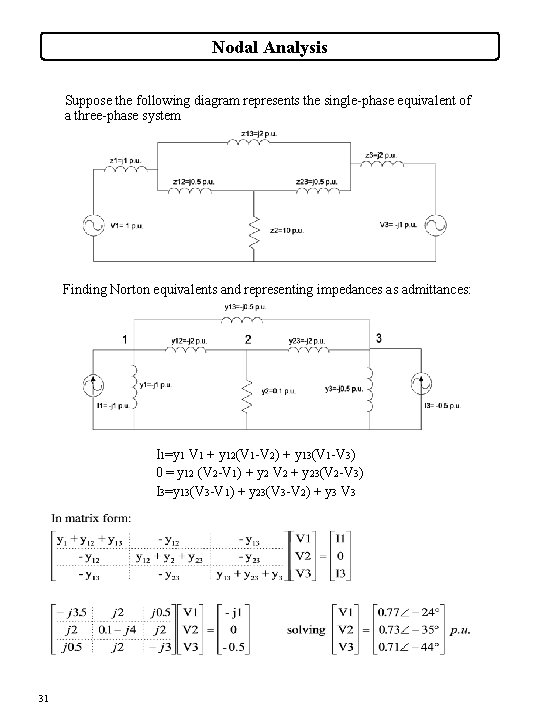
Nodal Analysis Suppose the following diagram represents the single-phase equivalent of a three-phase system Finding Norton equivalents and representing impedances as admittances: I 1=y 1 V 1 + y 12(V 1 -V 2) + y 13(V 1 -V 3) 0 = y 12 (V 2 -V 1) + y 2 V 2 + y 23(V 2 -V 3) I 3=y 13(V 3 -V 1) + y 23(V 3 -V 2) + y 3 V 3 31

General form of the nodal analysis Once the voltages are found, currents and powers are easily evaluated from the circuit. We have solved one of the phases of the three-phase system (e. g. phase ‘a’). Quantities for the other two phases are shifted 120 and 240 degrees under balanced conditions. Actual quantities can be found by multiplying the per unit values by their corresponding bases. 32