Pascals Triangle Pascals triangle is an array of

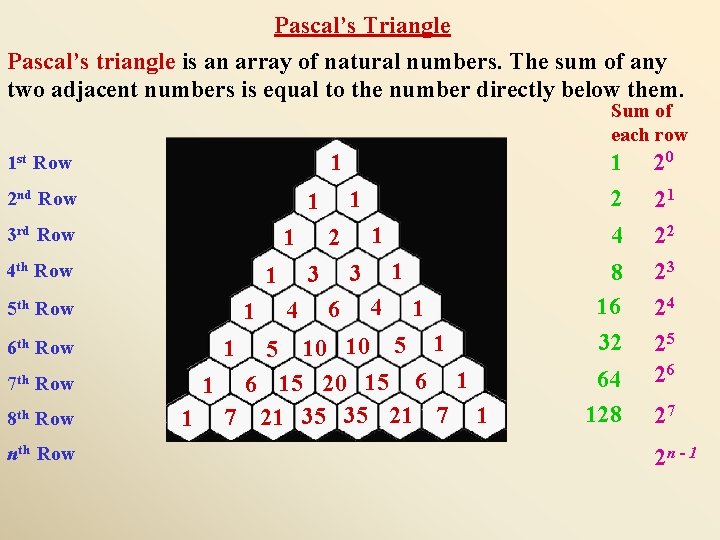
Pascal’s Triangle Pascal’s triangle is an array of natural numbers. The sum of any two adjacent numbers is equal to the number directly below them. Sum of each row 1 1 st Row 2 nd Row 1 4 th Row 7 th Row 8 th Row nth Row 4 1 1 3 6 4 1 2 3 1 5 th Row 6 th Row 1 1 3 rd Row 1 2 4 1 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 5 8 16 32 64 128 20 21 22 23 24 25 26 27 2 n - 1

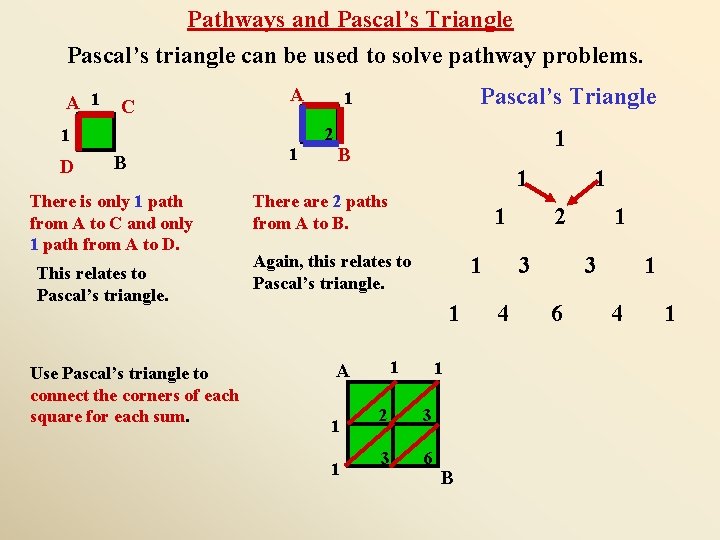
Pathways and Pascal’s Triangle Pascal’s triangle can be used to solve pathway problems. A 1 C B There is only 1 path from A to C and only 1 path from A to D. This relates to Pascal’s triangle. Use Pascal’s triangle to connect the corners of each square for each sum. 1 Pascal’s Triangle 1 2 1 D A 1 B 1 There are 2 paths from A to B. 1 Again, this relates to Pascal’s triangle. 1 1 1 A 1 1 1 2 3 3 6 B 1 2 3 4 1 3 6 1 4 1

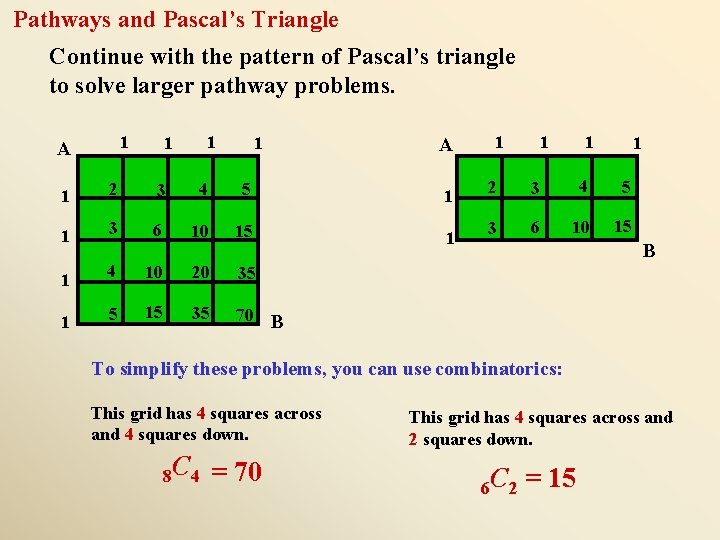
Pathways and Pascal’s Triangle Continue with the pattern of Pascal’s triangle to solve larger pathway problems. 1 A 1 1 2 3 4 5 1 3 6 10 15 4 10 20 35 5 15 35 70 B 1 1 A 1 1 1 2 3 4 5 3 6 10 15 B To simplify these problems, you can use combinatorics: This grid has 4 squares across and 4 squares down. 8 C 4 = 70 This grid has 4 squares across and 2 squares down. 6 C 2 = 15

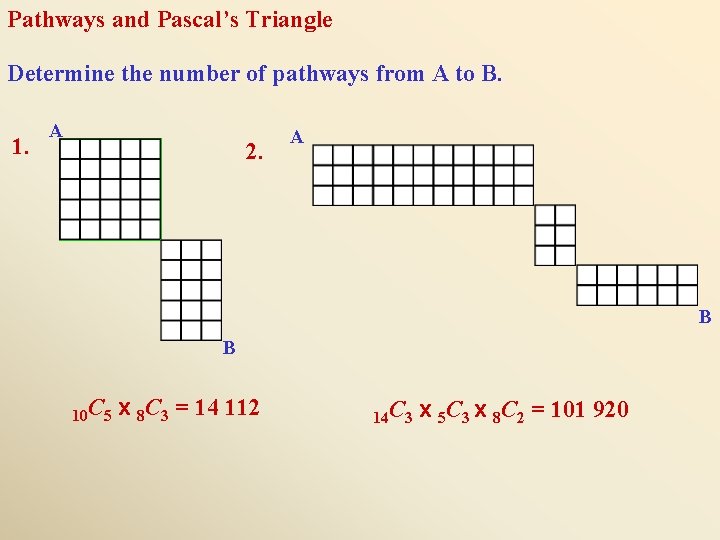
Pathways and Pascal’s Triangle Determine the number of pathways from A to B. 1. A 2. A B B 10 C 5 x 8 C 3 = 14 112 14 C 3 x 5 C 3 x 8 C 2 = 101 920

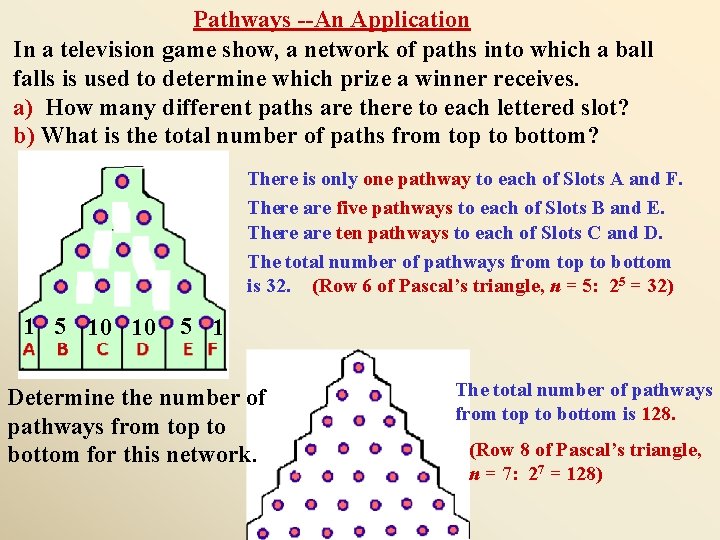
Pathways --An Application In a television game show, a network of paths into which a ball falls is used to determine which prize a winner receives. a) How many different paths are there to each lettered slot? b) What is the total number of paths from top to bottom? There is only one pathway to each of Slots A and F. There are five pathways to each of Slots B and E. There are ten pathways to each of Slots C and D. The total number of pathways from top to bottom is 32. (Row 6 of Pascal’s triangle, n = 5: 25 = 32) 1 5 10 10 5 1 Determine the number of pathways from top to bottom for this network. The total number of pathways from top to bottom is 128. (Row 8 of Pascal’s triangle, n = 7: 27 = 128)