Pascals Triangle How do we expand x15 quickly

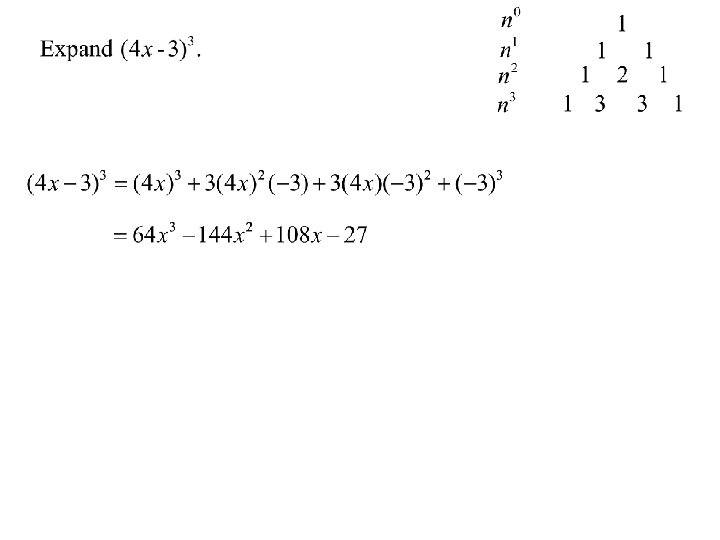
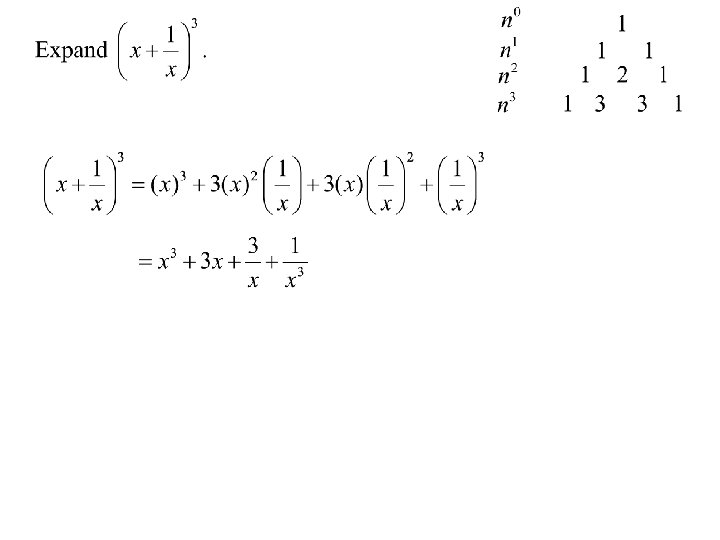



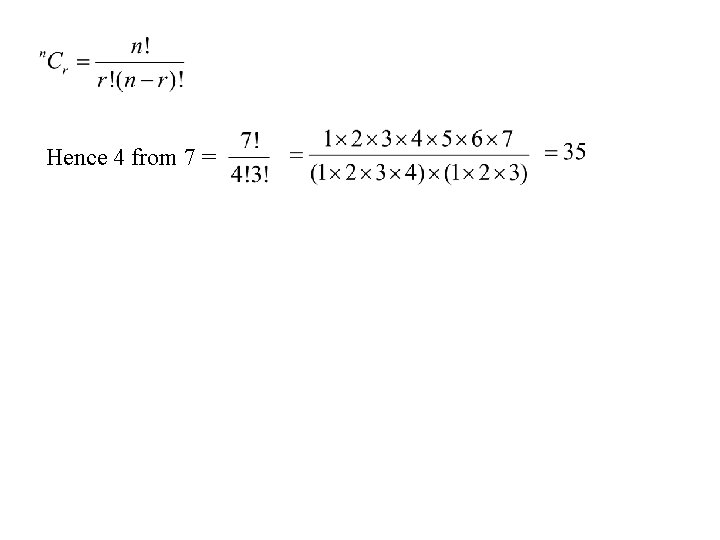













- Slides: 20

Pascal’s Triangle How do we expand (x+1)5 quickly? We can use Pascal’s triangle.
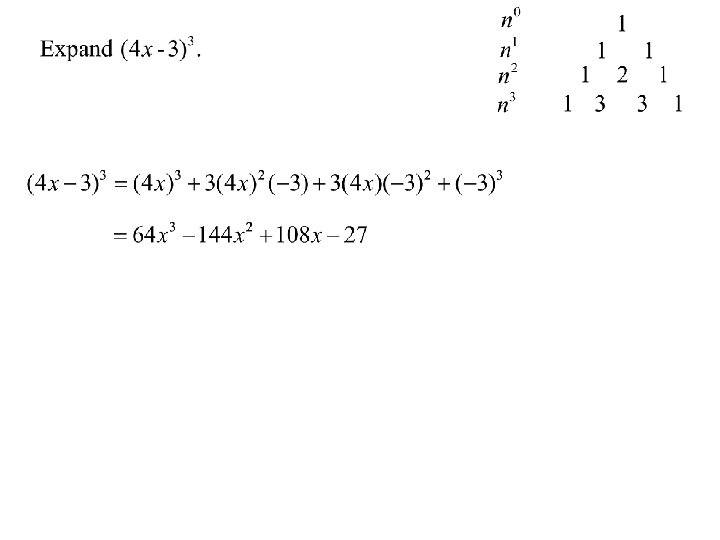
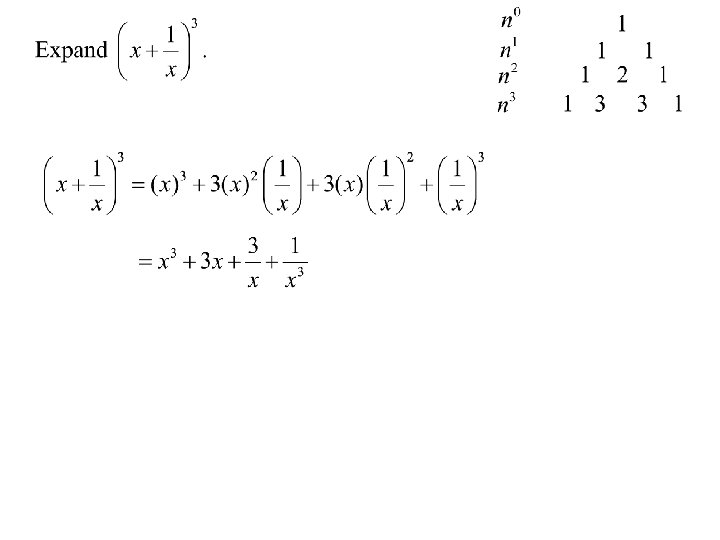

The Factorial Function n!=1 x 2 x 3 x…x (n-1) x n Six cyclists enter a race. All finish at different times. There is a first and second prize. (a) How many different ways can the cyclists finish the race? (a) How many different ways can prizes be awarded? (a) There are 6 different possible winners. For each winner there are 5 possible 2 nd places. ways of getting first and second. For each of these there are 4 possible 3 rd places.

(b) From (a) there are 30 ways of getting 1 st and 2 nd prizes. This can also be answered using factorials. This is a method of calculating the number of ways of arranging ‘r’ objects from a pool of ‘n’ objects. (2 from 6) ‘P’ refers to permutation. (b) Required arranging 2 from 6.

Ex. 2 From a palette of 7 colours, you can pick 4. How many different ways can this be done? The order of picking 4 does not matter here. Red, blue green and yellow is the same as green yellow red and blue. In this example we are selecting 4 from 7 but the order (arrangement) does not matter. There are 4! Ways of arranging four colours. This is a common problem (National Lottery) ‘C’ refers to combination. This is selection without arrangement.
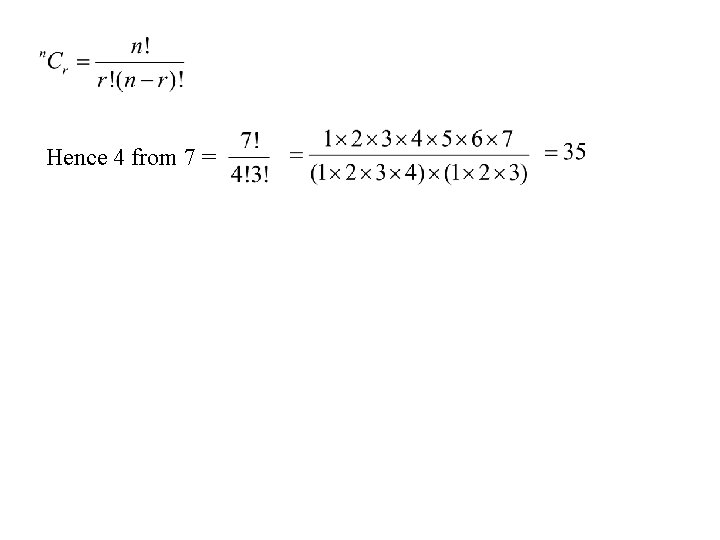
Hence 4 from 7 =

Hobson’s Choice! Hobson hired out horses. You paid your money and got the horse of your choice. (As long as it was the horse he offered you) How many ways can you pick one horse when there is only one horse to pick? Now we know the answer is 1 so,

What is the chance of winning the lottery? Just a little further notation:

A common Fact. Proof

I’ll let you investigate this !! Page 7 Exercise 2 B: Questions 1(a), 2, 4(a)(b), 5(a), 6(a), 7(a)(b)(d). TJ Exercise 1

The Binomial Theorem When generalised, This expansion is known as the Binomial Theorem

We can use the binomial theorem to expand brackets or to find a specific term in a polynomial.


MIA Page 9 Exercise 3 A TJ Exercise 2 Question 1

Further Expansions Consider each set of brackets separately. (trust me!!)

It is best to do this in tabular form to avoid errors

Further practice on page 11 Ex 3 B

Approximation Fact: We can use this fact to make useful approximations.

Page 13 Exercise 4 Page 14 Review