Pascals Triangle Andy Hopkins A Brief History Pascal

Pascal's Triangle Andy Hopkins

A Brief History… �Pascal was not the first to have discovered this triangle. �Al-Karaji knew of the triangle during his lifetime(953 -1029). �Also was discussed by Omar Khayyam. (It is known as Khayyam’s triangle in Iran) �Yang Hui discovered this triangle in China during his lifetime(1238 -1298). (Known as Yang Hui’s triangle in China). �Known as Tartaglia’s triangle in Italy (Tartaglia lived from 1500 -1577). �Pascal published his work in 1655. http: //en. wikipedia. org/wiki/Pascal_trian gle#History http: //milanovic. org/math/english/fi bo/fibo 0. html

Pascal’s work �Blaise Pascal published his paper with the help of Pierre de Fermat. �In the paper he explained everything that he had discovered about the triangle. �It starts with how to construct the triangle and then went on to list the 19 corollaries he found. http: //milanovic. org/math/english/fi bo/fibo 0. html Smith, David E. A Source Book in Mathematics. First ed. New York: Mc. Graw-Hill Book Company, Inc. , 1929.

How Pascal Starts the Triangle � What Pascal did was took a point (which he called G) and drew a line to the right of it and down from it. � Then he drew lines from one line to the other to create 10 different triangles. � He then proceeded to draw lines parallel to each line that was constructed from point G to create cells. � After this he started with a number that he calls the generator. This, of course, is the number one. However, it can be a different number than one if you want to construct a different triangle. � The final thing that he states is that you can find the other cells based on this rule: The numbers of each cell are equal to the sum of the previous cells to the left and above the cell you are trying to find. Smith, David E. A Source Book in Mathematics. First ed. New York: Mc. Graw-Hill Book Company, Inc. , 1929.

Pascal’s Corollaries �To do all of Pascal’s corollaries in a paper or a presentation would take a lot of time. I decided to do them on corollaries 1 -3, 5 -9, and 11. �The first one just states that the number one is in each cell of the first row and column. �The next two are similar in saying that if you take consecutive numbers in a row or column and add them up your result will be in the next row or column. We call this the Hockey Stick pattern. Smith, David E. A Source Book in Mathematics. First ed. New York: Mc. Graw-Hill Book Company, Inc. , 1929. http: //ptri 1. tripod. com/

Corollaries con’t �There also corollaries that use previous corollaries to help solve the current one. �Corollary 7 says that the sum of a row divided by 2 is equal to the sum of the previous row. �Corollary 8 says that the sum of each row is a number in the geometric progression (1, 2, 4, 8, 16, 32…). This is true if we add up the numbers in each row and divide by 2 (corollary 7). Smith, David E. A Source Book in Mathematics. First ed. New York: Mc. Graw. Hill Book Company, Inc. , 1929.

Examples of previous triangles. This is a pre-Pascal triangle in Japanese http: //cas. umkc. edu/math/Extra Caption. htm

This is a pre-Pascal Chinese triangle. http: //milanovic. org/math/english /fibo 0. html

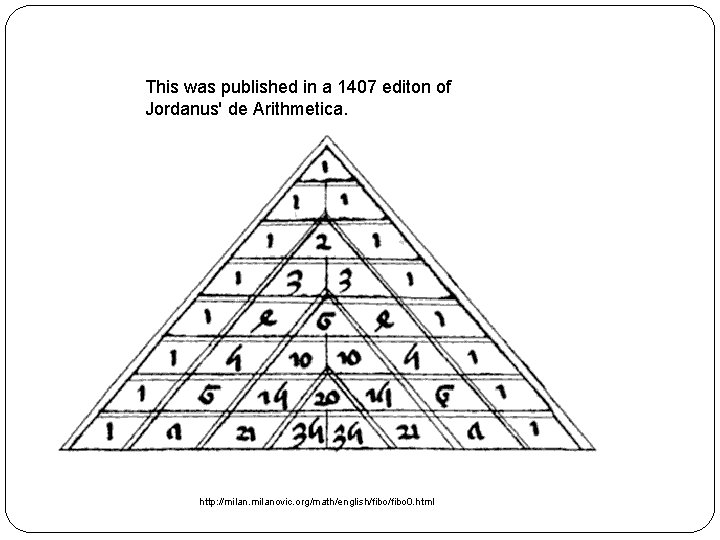
This was published in a 1407 editon of Jordanus' de Arithmetica. http: //milanovic. org/math/english/fibo 0. html

This was published in 1544 by Michael Stifel of Germany http: //milanovic. org/m ath/english/fibo 0. html

This table was published in 1636 by Father Marin Mersenne. http: //milanovic. org/m ath/english/fibo 0. html

This is Pascal’s original triangle. http: //threesixty 3 60. wordpress. co m/2007/11/