Party Problem The simplest example of Ramsey theory

Party Problem The simplest example of Ramsey theory. It is also known as the ‘Maximum Clique Problem’. A clique of a graph is a complete sub graph of the main graph, and the clique of largest possible size is referred to as a maximum clique. Course Name: Graph Theory Author(s) : Phani Swathi Chitta Mentor: Prof. Saravanan Vijayakumaran Level(UG/PG): UG *The contents in this ppt are licensed under Creative Commons Attribution-Non. Commercial-Share. Alike 2. 5 India license

Learning Objectives After interacting with this Learning Object, the learner will be able to: • Explain the proof for a problem called ‘Party problem’ of Ramsey theory

Definitions of the components/Keywords: 1 2 • The ‘Party Problem’ is also called ‘Theorem on Friends and Strangers’. • Statement of theorem is: Prove that at a party of six people there at least three mutual friends or at least there are three mutual strangers. • We can phrase the problem in graph-theoretic language as follows: 3 4 5 - Let the 6 nodes A - F stand for the 6 people in the party. - Let the edges be colored or blue depending on whether the two people represented by the nodes connected by the edge are mutual strangers or mutual friends, respectively.

1 Master Layout 1 2 indicates know each other indicates don’t know each other 3 4 5 • Give Play, Next and Reset buttons

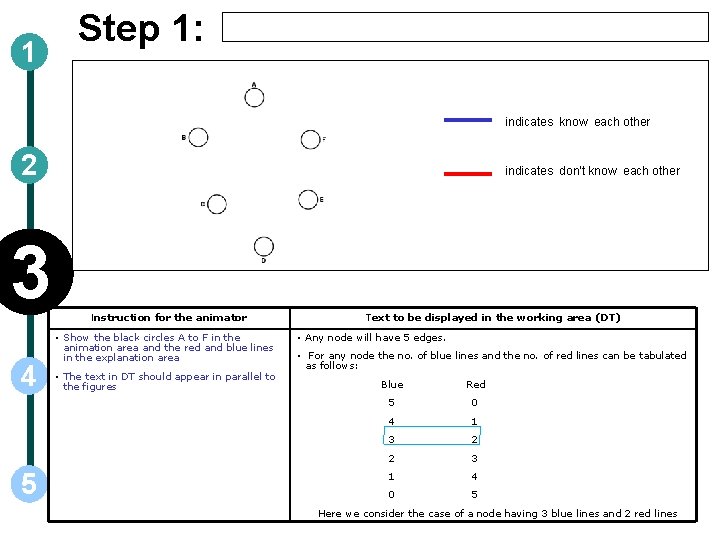
1 Step 1: indicates know each other 2 3 4 5 indicates don’t know each other Instruction for the animator • Show the black circles A to F in the animation area and the red and blue lines in the explanation area • The text in DT should appear in parallel to the figures Text to be displayed in the working area (DT) • Any node will have 5 edges. • For any node the no. of blue lines and the no. of red lines can be tabulated as follows: Blue Red 5 0 4 1 3 2 2 3 1 4 0 5 Here we consider the case of a node having 3 blue lines and 2 red lines

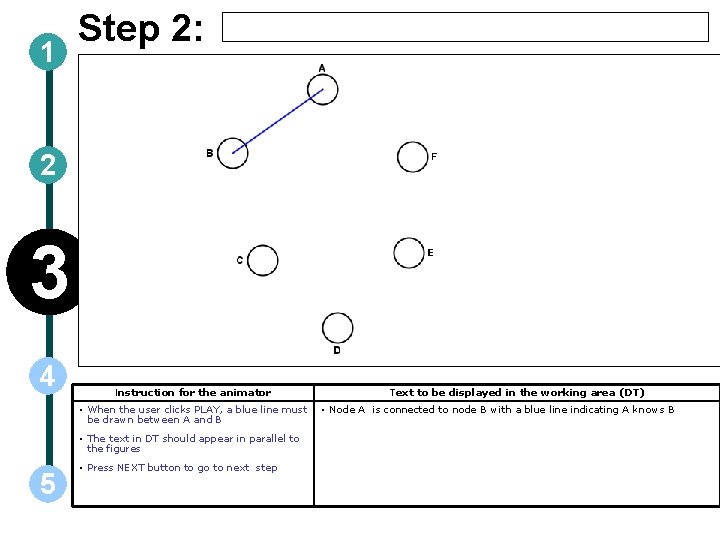
1 Step 2: 2 3 4 Instruction for the animator • When the user clicks PLAY, a blue line must be drawn between A and B • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to node B with a blue line indicating A knows B

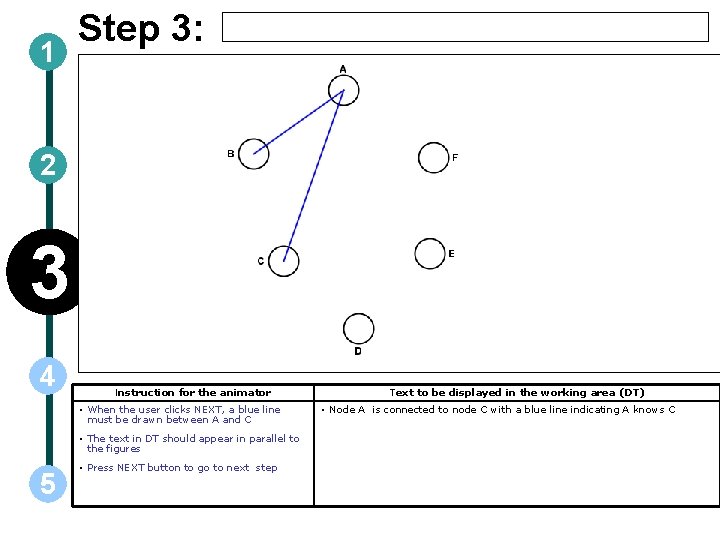
1 Step 3: 2 3 4 Instruction for the animator • When the user clicks NEXT, a blue line must be drawn between A and C • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to node C with a blue line indicating A knows C

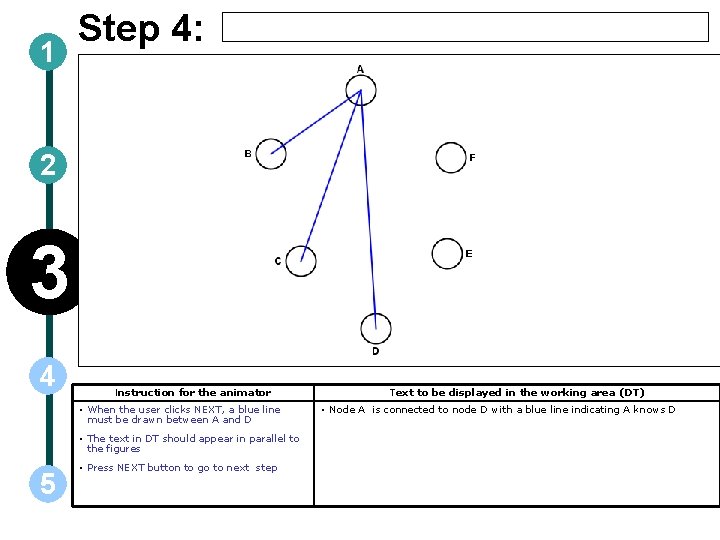
1 Step 4: 2 3 4 Instruction for the animator • When the user clicks NEXT, a blue line must be drawn between A and D • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to node D with a blue line indicating A knows D

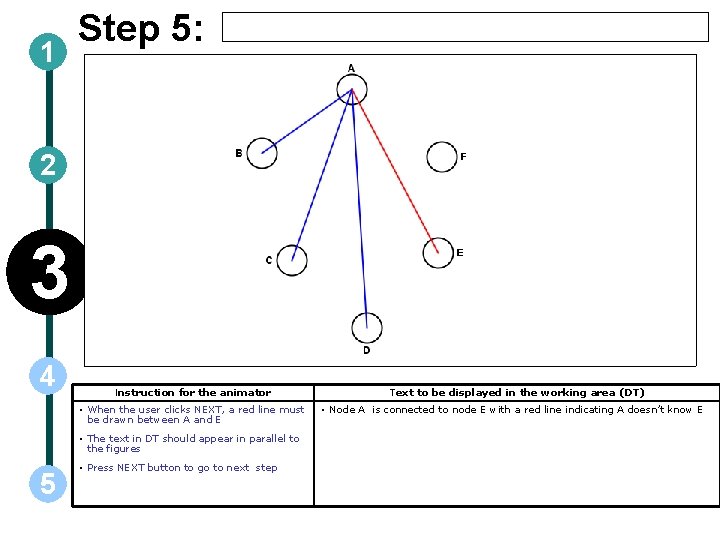
1 Step 5: 2 3 4 Instruction for the animator • When the user clicks NEXT, a red line must be drawn between A and E • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to node E with a red line indicating A doesn’t know E

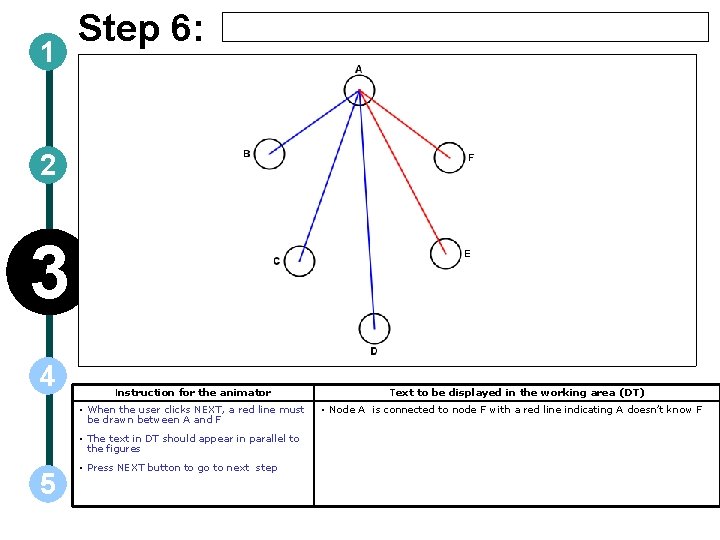
1 Step 6: 2 3 4 Instruction for the animator • When the user clicks NEXT, a red line must be drawn between A and F • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to node F with a red line indicating A doesn’t know F

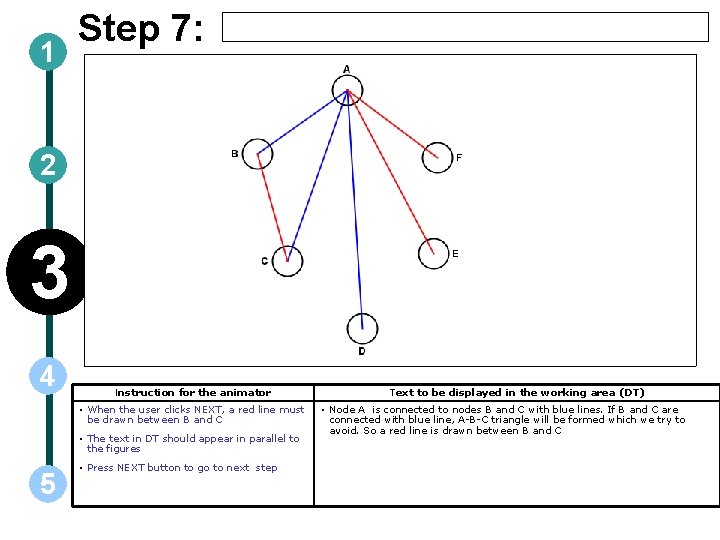
1 Step 7: 2 3 4 Instruction for the animator • When the user clicks NEXT, a red line must be drawn between B and C • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to nodes B and C with blue lines. If B and C are connected with blue line, A-B-C triangle will be formed which we try to avoid. So a red line is drawn between B and C

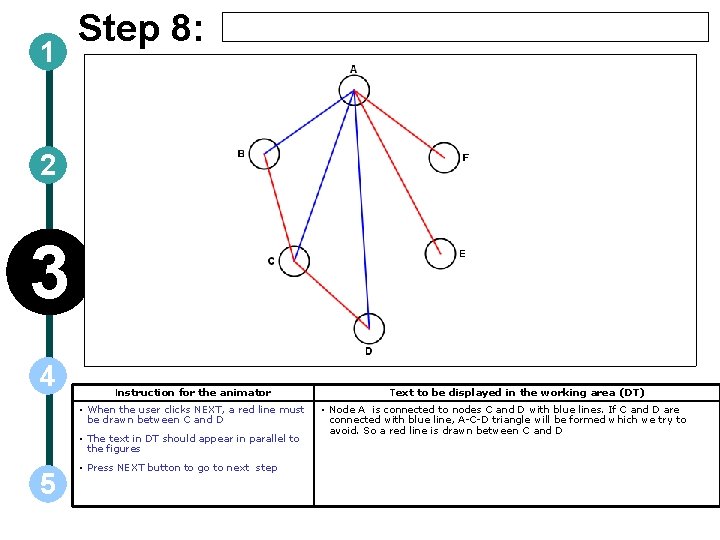
1 Step 8: 2 3 4 Instruction for the animator • When the user clicks NEXT, a red line must be drawn between C and D • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to nodes C and D with blue lines. If C and D are connected with blue line, A-C-D triangle will be formed which we try to avoid. So a red line is drawn between C and D

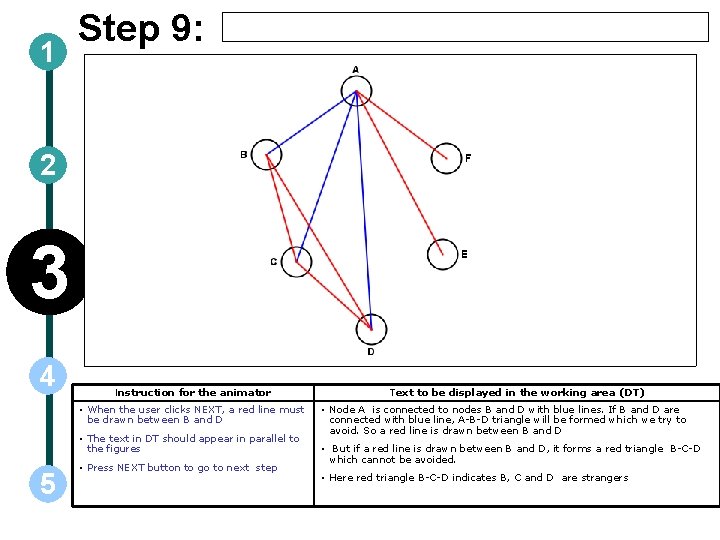
1 Step 9: 2 3 4 Instruction for the animator • When the user clicks NEXT, a red line must be drawn between B and D • The text in DT should appear in parallel to the figures 5 • Press NEXT button to go to next step Text to be displayed in the working area (DT) • Node A is connected to nodes B and D with blue lines. If B and D are connected with blue line, A-B-D triangle will be formed which we try to avoid. So a red line is drawn between B and D • But if a red line is drawn between B and D, it forms a red triangle B-C-D which cannot be avoided. • Here red triangle B-C-D indicates B, C and D are strangers

1 Step 10: 2 3 4 Instruction for the animator • The text in DT should appear at last • Then give End of animation and then the RESET button has to be enabled • Press RESET to stop the animation 5 Text to be displayed in the working area (DT) • Thus we conclude that in a party of 6 guests there will be at least 3 mutual friends or at least 3 mutual strangers

Electrical Engineering Slide 1 Introduction Slide 3 Definitions Slide 16, 17, 18, 19 Analogy Slide 20 Want to know more… Test your understanding Lets Sum up (summary) (Further Reading) (questionnaire) Interactivity: Try it yourself Depending on the no. of nodes selected by the user the figure appears Ø Please select no. of nodes and Press PLAY button to start the animation ØPlease select color(red or blue) and click on any two nodes to join them. Default color is red Ø Give drop down to select no. of nodes In the explanation area • When a line is drawn between nodes the below statement should appear - Edge is drawn between XX node and YY node • When the triangle is formed the below statement should appear ( in red color or blue color depending on the color of the triangle) - Triangle is formed • If all the lines are drawn and no triangle is formed then print the below statement - Can’t find three people who know each other or don’t know each other • If all the nodes are connected with lines then - All the edges are drawn • 6 nodes • 5 nodes • 4 nodes Ø Give hint for each node as: Ø Hint: Possible Edges • 4 nodes: Edges can be drawn from A-B, A-C, A-D, B-C, B-D, C-D • 5 nodes: Edges can be drawn from A-B, A-C, A-D, A-E, B-C, B-D, B-E, C-D, C-E, D-E • 6 nodes: Edges can be drawn from A-B, A-C, A-D, A-E, A-F, B-C, B-D, B-E, B-F, C-D, C-E, C-F, D-E, D-F, E-F 15 Credits

Questionnaire 1 2 3 4 5 1. In a party of 6 people, is it possible to have 3 mutual friends and 3 mutual strangers simultaneously? Answers: a) Yes b) No

Questionnaire 1 2 2. In a party of 5 people, is it always true that there at least 3 mutual friends or strangers? 3 Answers: a) 4 5 Yes b) No

Questionnaire 1 2 3. There are 6 cities connected by either rail or road(only either of them but not both). How many cities can at least be connected by rail? 3 Answers: a) 4 5 3 b) 4 c) 5 d) 6

Questionnaire 1 2 4. There are 6 cities connected by either rail or road(only either of them but not both). How many cities can at least be connected by road? 3 Answers: a) 4 5 3 b) 4 c) 5 d) 6

Links for further reading Reference websites: http: //mathworld. wolfram. com/Ramsey. Number. html http: //mathworld. wolfram. com/Ramsey. Theory. html http: //www. cs. ucsb. edu/~rich/class/cs 290 I-grid/notes/Ramsey/ http: //www. cut-the knot. org/Curriculum/Combinatorics/Three. Or. Three. shtml http: //en. wikipedia. org/wiki/Theorem_on_friends_and_strangers http: //en. wikipedia. org/wiki/Clique_problem Books: GRAPH THEORY –Harary, Narosa Publishing House