PARTS OF ANGLES AND DMS Dr Shildneck Angles

PARTS OF ANGLES AND DMS Dr. Shildneck

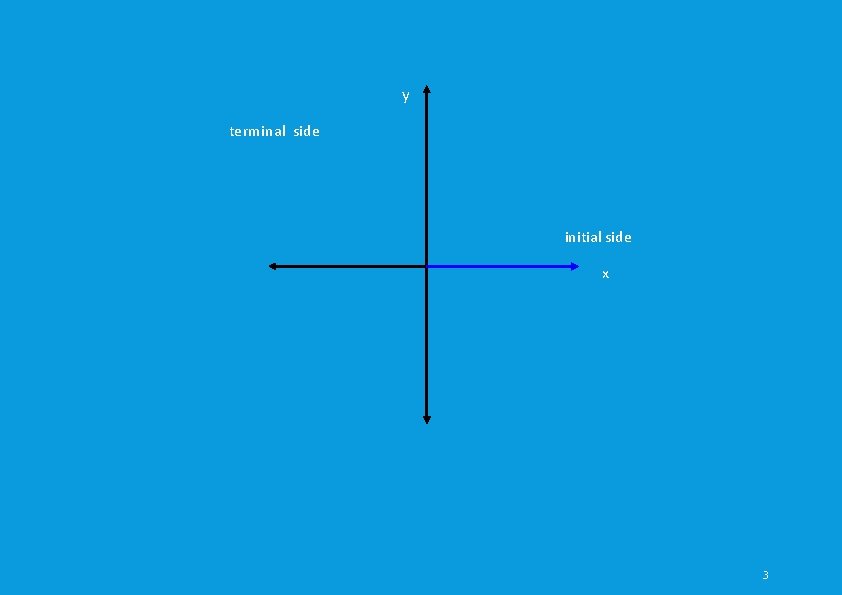
Angles and Their Measures Recall that an angle is defined as two non‐colinear rays that share a common endpoint, called the vertex An angle in (circle) trigonometry has a fixed (starting) side, called the i nitial side ‐ which points in the direction of the positive x‐axis. The v ertex is the origin. The second side is rotated (like the hands of a clock) about the vertex. This side is called the t erminal side An angle with this placement is said to be in S tandard Position 2

y terminal side initial side x 3

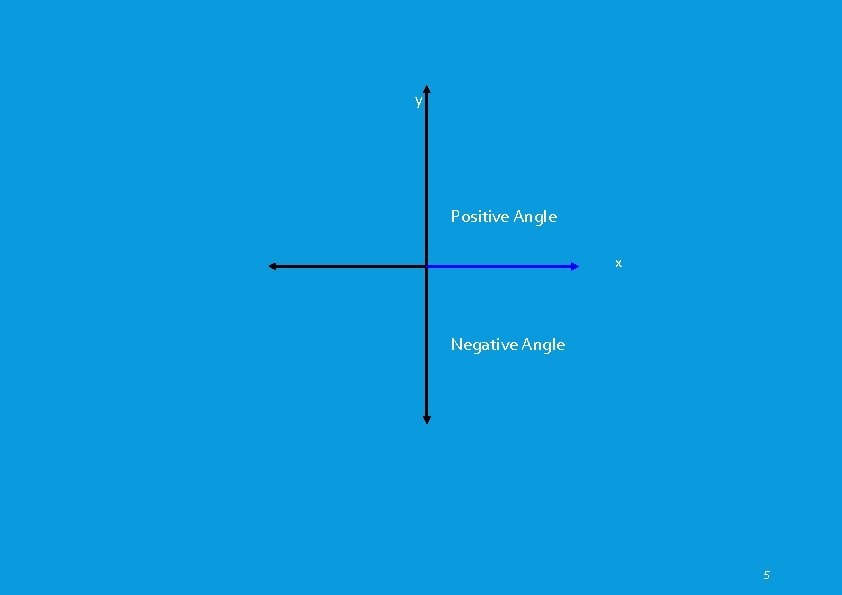
The measure of the angle describes the amount and direction of the rotation necessary to move from the initial side to the terminal side. A positive angle indicates that the terminal side has been rotated counter‐clockwise. A negative angle indicates that the terminal side has been rotated clockwise. 4

y Positive Angle x Negative Angle 5

The most common angular unit of measure is called the "degree, " which is equivalent to 1/360 of a full rotation around a circle. Key (basic) Angle Measures (counterclockwise) • 0 o ‐ No rotation • • 90 o ‐ ¼ of a rotation 180 o ‐ ½ of a rotation 270 o ‐ ¾ of a rotation 360 o ‐ 1 full rotation (back to the initial side) These angles are called the "Quadrantal Angles" Angles since they end on the boundaries between the quadrants of the coordinate plane. 6

Angles based on rotation can be any size and either sign (positive or negative). If you were to continue to rotate the terminal side past 360 o, you would simply continue to add (or subtract if negative) to the angle. 120 o -240 o **Note that Additional rotations are indicated by a rotation mark. 7

Degrees – Not exact Obviously the terminal side can end up not on a "degree" mark. Thus, you can have measures that use parts of a degree. There are two ways that this might be indicated. 1. Decimal form: This form simply indicates the "fractional" part of the degree. Example: 35. 75 o ‐ means 35 degrees and 3/4 more of a degree 8

2. Degrees-Minutes-Seconds (DMS) A more formal "part form" of a degree uses minutes and seconds. The conversion ratio between decimal form and DMS is like that of a clock. 1 degree is made up of 60 minutes ( 1 o = 60') 1 minute is made up of 60 seconds (1' = 60") 9

Converting by Hand – Dimensional Analysis (1) Convert 65. 755 o into DMS form Answer: _____o ____’ _____” How many “whole” seconds? degrees? minutes? 65 0. 3 minutes x 60 seconds/1 minute == 1845 seconds 0. 755 degrees x 60 minutes/1 degree 45. 3 minutes (2) Convert 20 o 21' into Decimal form Answer: ___ o How many “part” “whole” degrees? 20 35 degrees 21 minutes x 1 degree/60 minutes = 0. 35 10

Converting by Calculator Convert 65. 75382 o into DMS form Type 65. 75382 into your calculator. Press [2 nd][APPS] (angle) Press [4] (>DMS) o ANSWER: 65 45’ 13. 752” Press [ENTER] Convert 20 o 15' 54" into Decimal form Type 20, Press [2 nd][APPS][1] Type 15, Press [2 nd][APPS][2] Type 54, Press [ALPHA][+] Press [ENTER] ANSWER: 20. 265 o 10

ASSIGNMENT 2 WS ‐ Measures of Angles 11