partitioned regression Fundamentals of PROGRAM EVALUATION JESSE LECY

partitioned regression Fundamentals of PROGRAM EVALUATION JESSE LECY

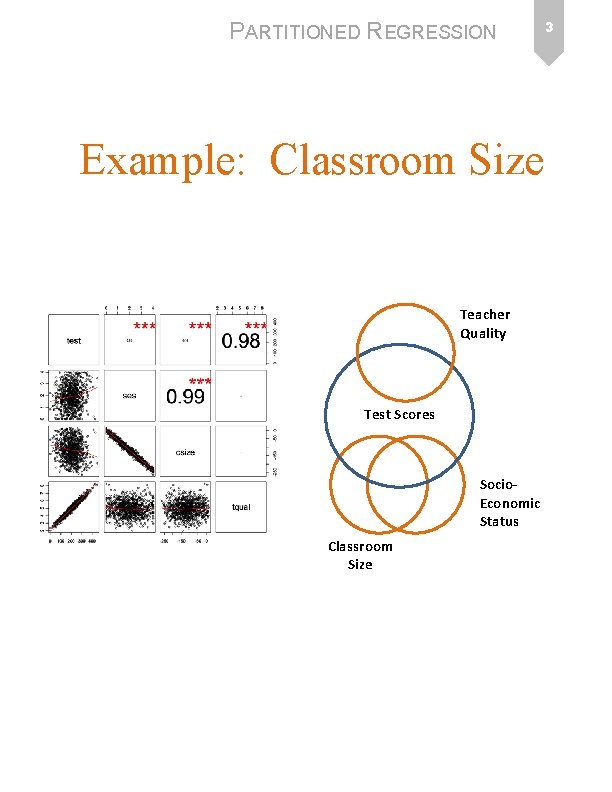
PARTITIONED REGRESSION Example: Classroom Size Why are slopes and standard errors changing when we add “control” variables? 2

PARTITIONED REGRESSION Example: Classroom Size Teacher Quality Test Scores Socio. Economic Status Classroom Size 3

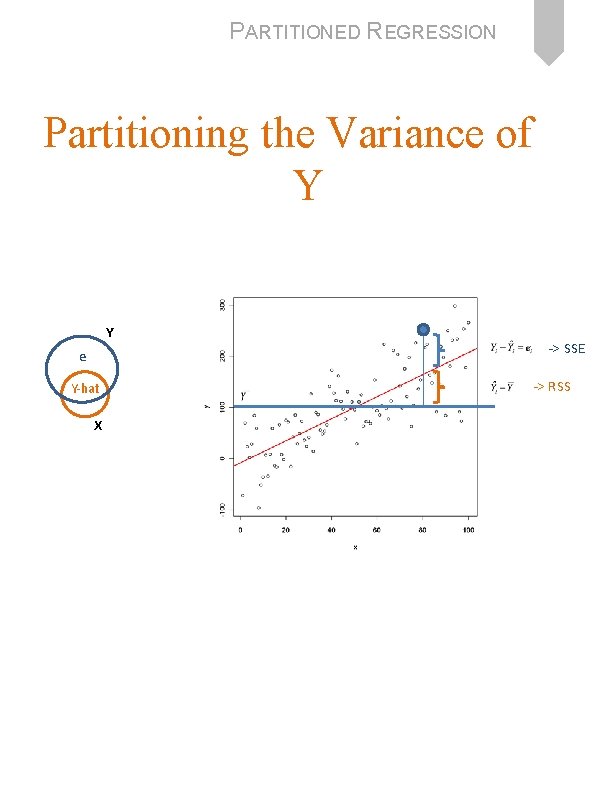
PARTITIONED REGRESSION Partitioning the Variance of Y Y e Y-hat X -> SSE -> RSS

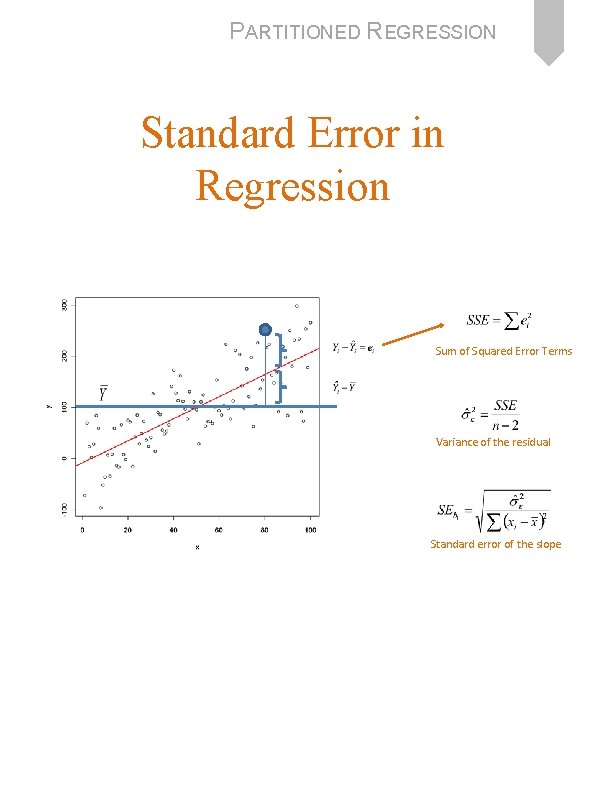
PARTITIONED REGRESSION Standard Error in Regression Sum of Squared Error Terms Variance of the residual Standard error of the slope

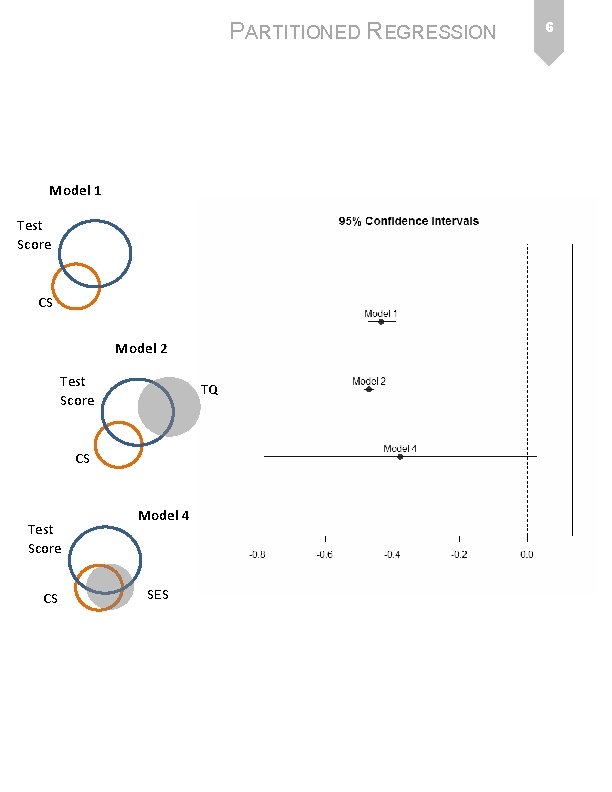
PARTITIONED REGRESSION Model 1 Test Score CS Model 2 Test Score TQ CS Test Score CS Model 4 SES 6

PARTITIONED REGRESSION 7

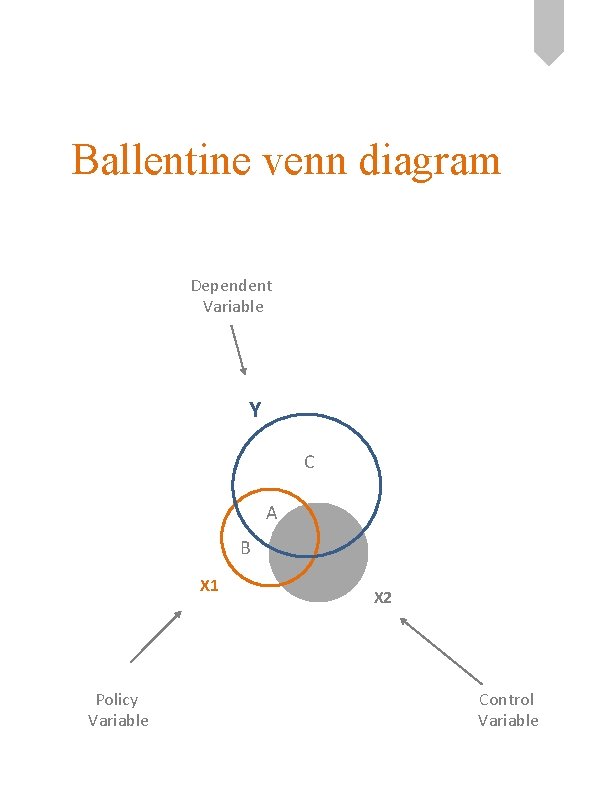
Ballentine venn diagram Dependent Variable Y C A B X 1 Policy Variable X 2 Control Variable

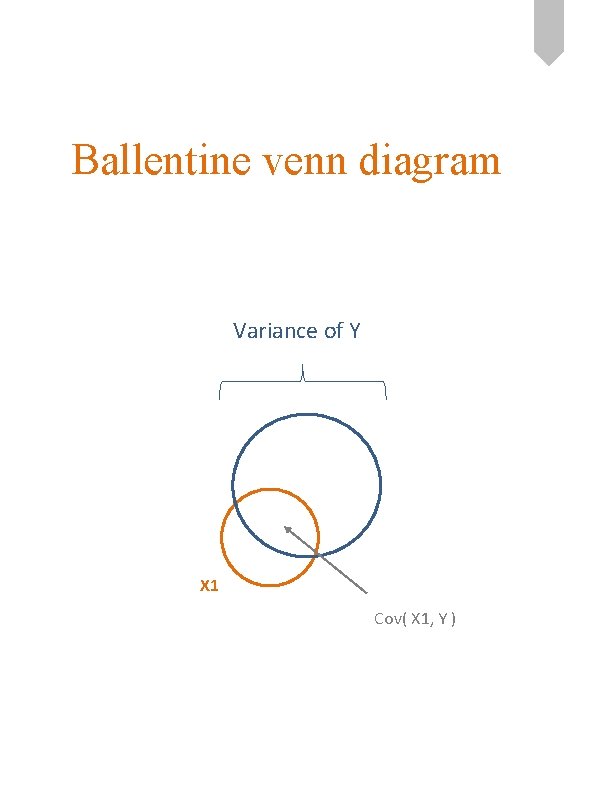
Ballentine venn diagram Variance of Y X 1 Cov( X 1, Y )

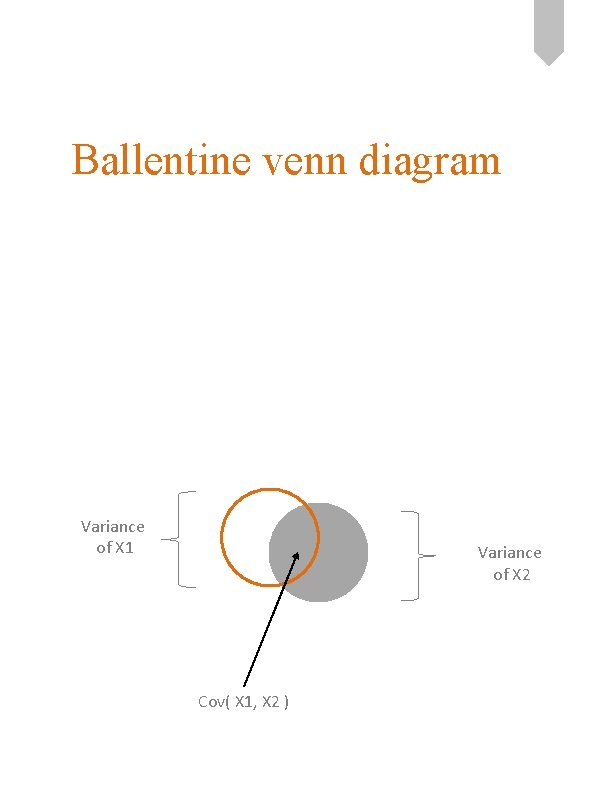
Ballentine venn diagram Variance of X 1 Variance of X 2 Cov( X 1, X 2 )

Ballentine venn diagram C = Unexplained Portion of Y (the residual) A = Cov( X 1, Y) after removing effects of X 2 (“controlling for”) Y C A B X 1 A + B = Variance of X 1 after controlling for X 2

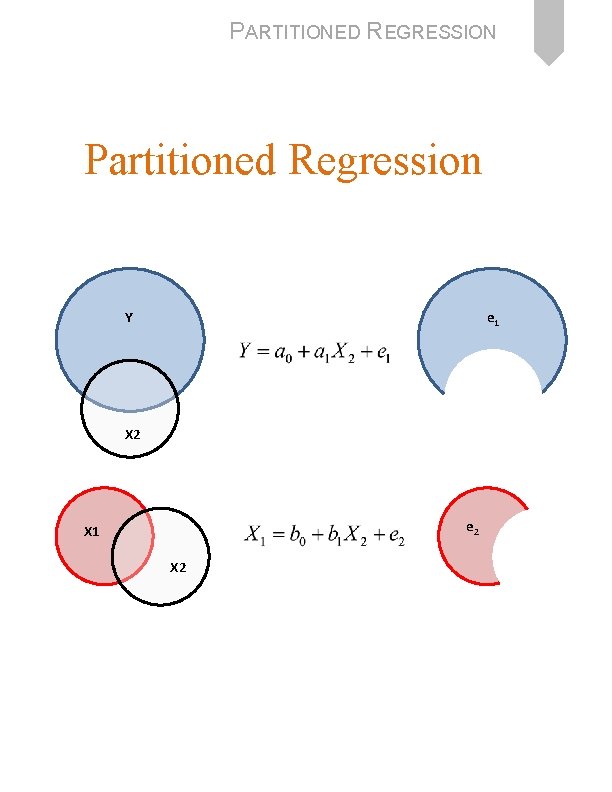
PARTITIONED REGRESSION Partitioned Regression Y e 1 X 2 e 2 X 1 X 2

PARTITIONED REGRESSION Partitioned Regression e 1 C A e 2 B 13

PARTITIONED REGRESSION Why can we do this? The residual is just another variable. The order of operations is important in partitioned regression.

PARTITIONED REGRESSION Note: Multiple Regression Context If there is more than one control variable make sure you cleanse all of the nuisance variance from both your dependent variable and your policy variable.

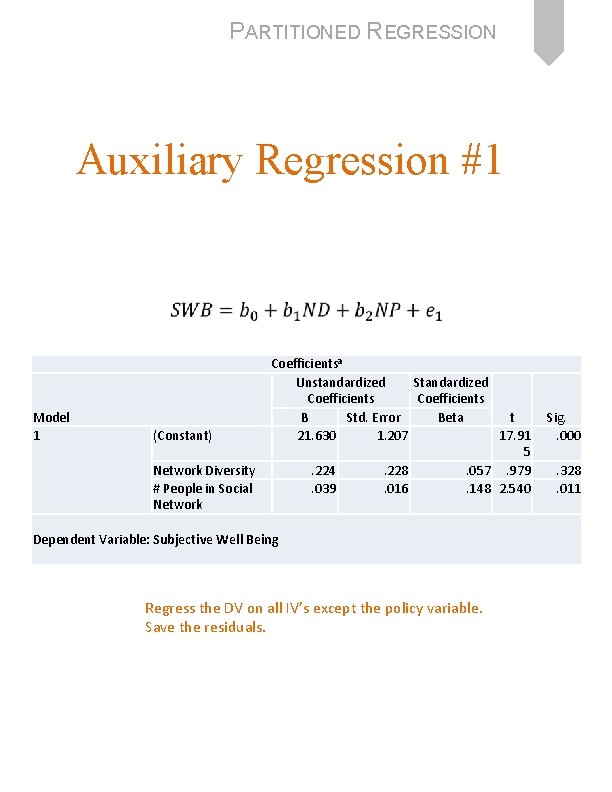
PARTITIONED REGRESSION 16 Example 1: “policy variable” Model 1 (Constant) Perceived Social Support Network Diversity # People in Social Network Coefficientsa Unstandardized Standardized Coefficients t Sig. B Std. Error Beta -1. 507 2. 633 -. 572. 567 . 310 . 032 . 460 9. 645. 000 -. 215. 023 . 210. 014 -. 055. 087 -1. 025. 306 1. 654. 099 Dependent Variable: Subjective Well Being

PARTITIONED REGRESSION Auxiliary Regression #1 Model 1 (Constant) Network Diversity # People in Social Network Coefficientsa Unstandardized Standardized Coefficients t B Std. Error Beta 21. 630 1. 207 17. 91 5. 224. 228. 057. 979. 039. 016. 148 2. 540 Dependent Variable: Subjective Well Being Regress the DV on all IV’s except the policy variable. Save the residuals. Sig. . 000. 328. 011

PARTITIONED REGRESSION Auxiliary Regression #1 Coefficients a Standardized Unstandardized Coefficients Model 1 B (Constant) Std. Error 21. 630 1. 207 Network Diversity . 224 . 228 # People in Social . 039 . 016 Network a. Dependent Variable: Subjective Well Being Coefficients t Beta Sig. 17. 915 . 000 . 057 . 979 . 328 . 148 2. 540 . 011

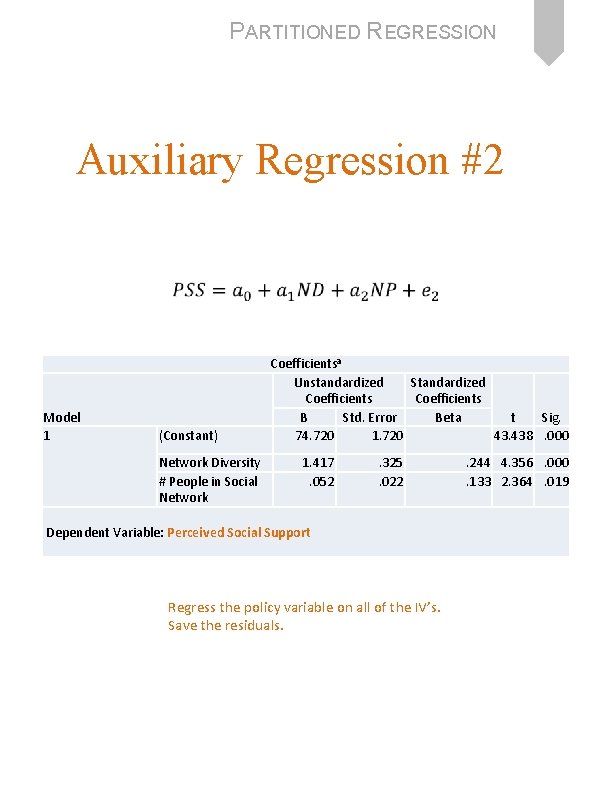
PARTITIONED REGRESSION Auxiliary Regression #2 Model 1 (Constant) Network Diversity # People in Social Network Coefficientsa Unstandardized Standardized Coefficients t Sig. B Std. Error Beta 74. 720 1. 720 43. 438. 000 1. 417. 052 . 325. 022 Dependent Variable: Perceived Social Support Regress the policy variable on all of the IV’s. Save the residuals. . 244 4. 356. 000. 133 2. 364. 019

PARTITIONED REGRESSION Partitioned Regression Regress the residuals on each other. Model 1 (Constant) Unstandardized Residual Coefficientsa Unstandardized Standardized Coefficients B Std. Error Beta 2. 369 E-15. 253 . 310 . 032 . 441 t. 000 9. 670 Sig. 1. 000 Dependent Variable: Unstandardized Residual We have recovered the original slope!

PARTITIONED REGRESSION Why is this important? • It illustrates the idea of statistical controls in policy work – get rid of the nuisance variance! • Provides insight into the regression error term. • Serves as a tool for future methods (instrumental variables). • It paved the way for modern computational econometrics.

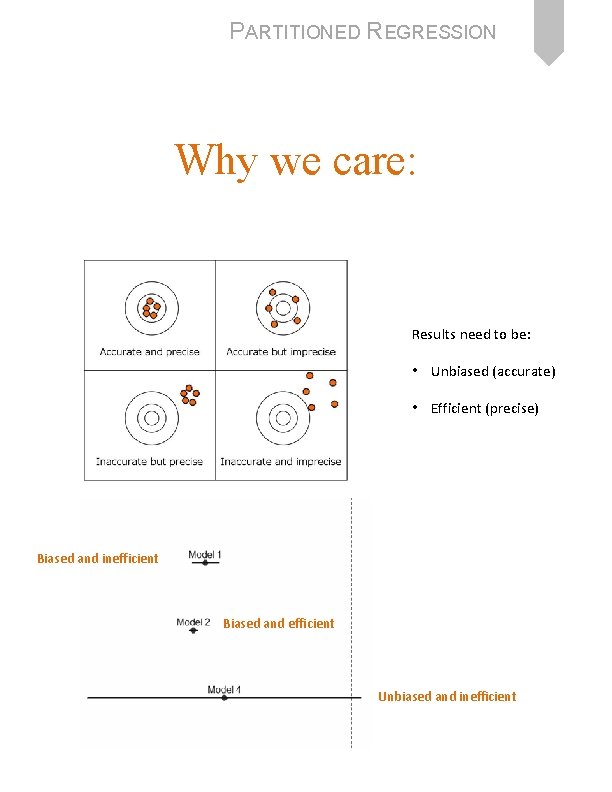
PARTITIONED REGRESSION Why we care: Results need to be: • Unbiased (accurate) • Efficient (precise) Biased and inefficient Biased and efficient Unbiased and inefficient

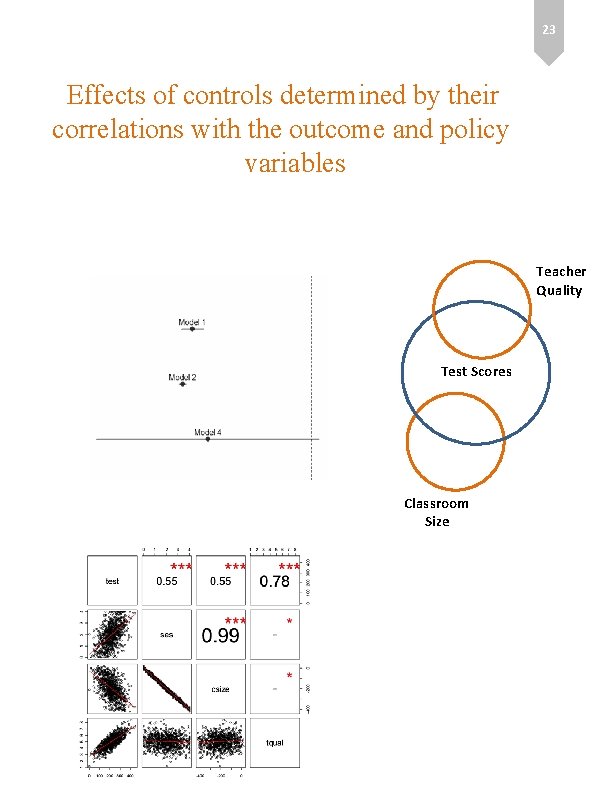
23 Effects of controls determined by their correlations with the outcome and policy variables Teacher Quality Test Scores Classroom Size

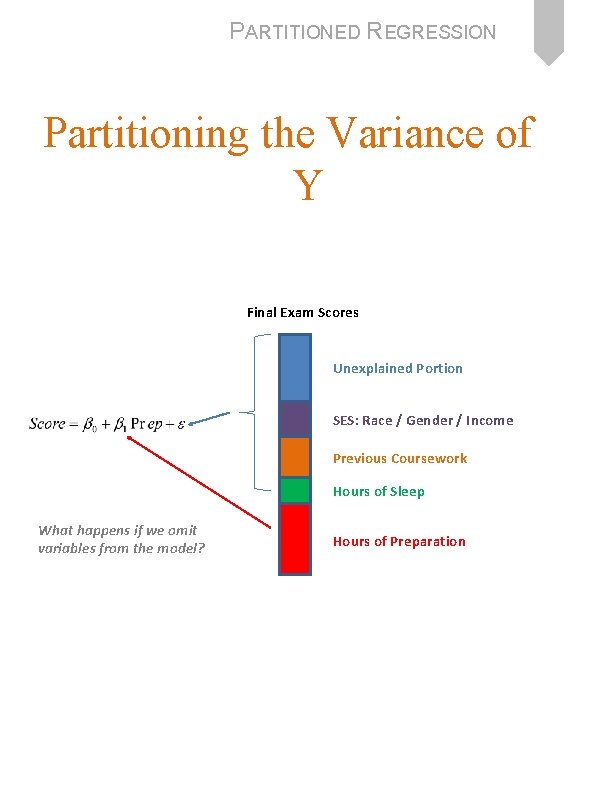
PARTITIONED REGRESSION Partitioning the Variance of Y Final Exam Scores Unexplained Portion SES: Race / Gender / Income Previous Coursework Hours of Sleep What happens if we omit variables from the model? Hours of Preparation

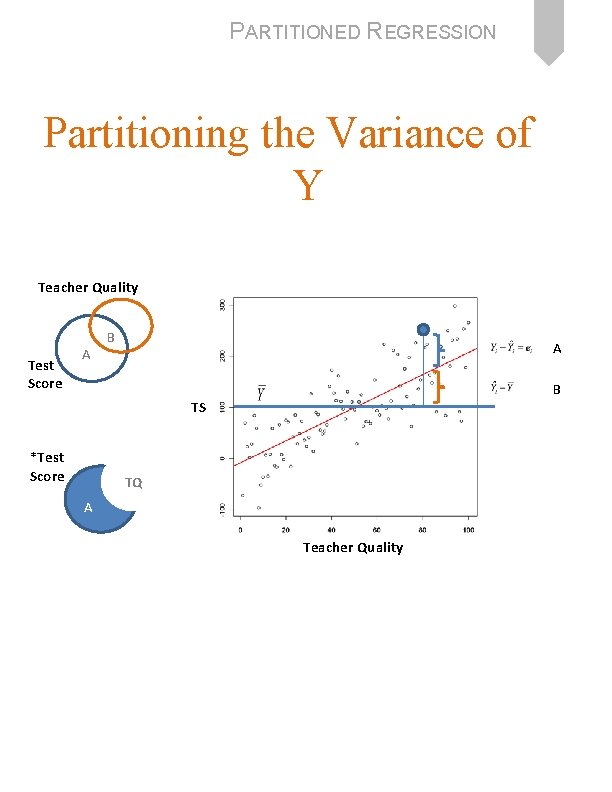
PARTITIONED REGRESSION Partitioning the Variance of Y Teacher Quality Test Score A B TS *Test Score TQ A Teacher Quality

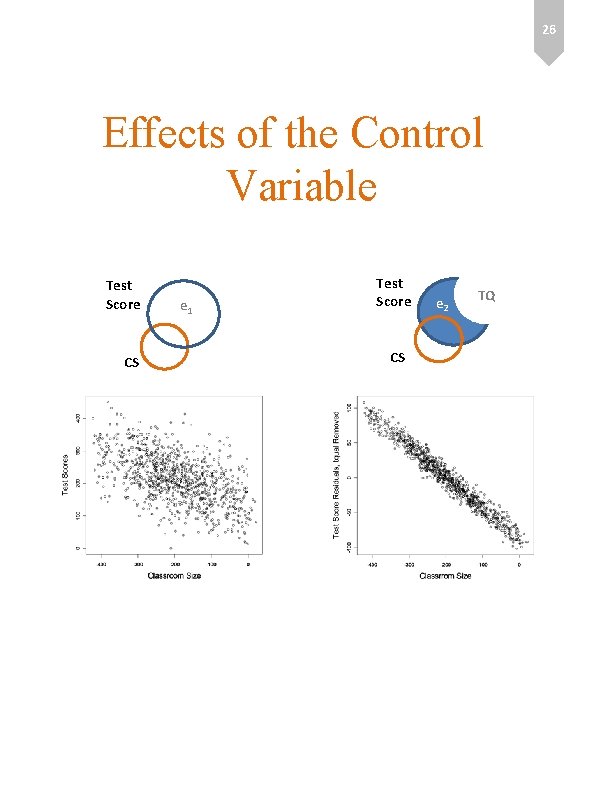
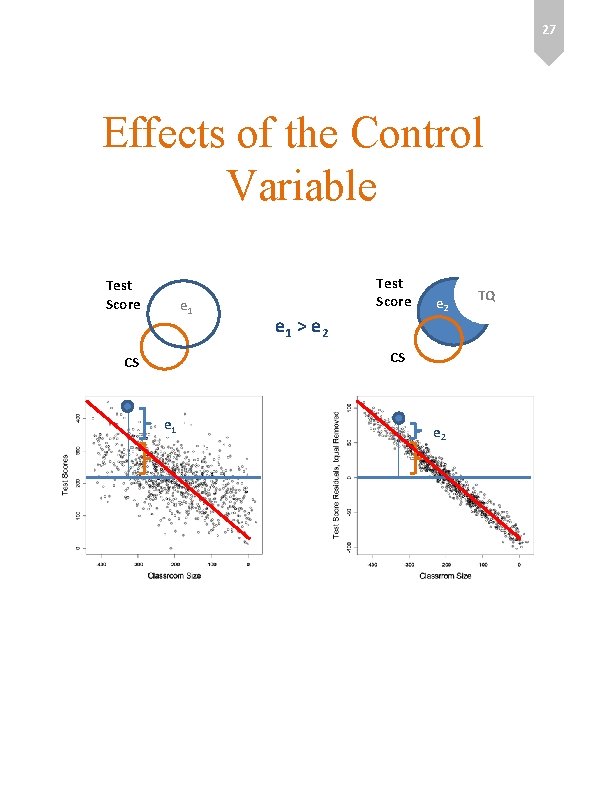
26 Effects of the Control Variable Test Score CS e 1 Test Score CS e 2 TQ

27 Effects of the Control Variable Test Score e 1 > e 2 CS CS e 1 e 2 TQ

PARTITIONED REGRESSION PARTITIONING Y WITH MULTIPLE VARIABLES 28

PARTITIONED REGRESSION What happens to slopes and standard errors when we add more variables? Y A X D B C Z

PARTITIONED REGRESSION Multiple Regression Mechanics: SLOPE Y A X D B C Z The formula for the slope is different when you add more variables

PARTITIONED REGRESSION Multiple Regression Mechanics: STANDARD ERRORS Y A B X Z The unexplained variance is different when you add more variables