Partition Functions for Independent Particles We now consider

Partition Functions for Independent Particles • We now consider the partition function for independent particles, i. e. , particles that do not in any way interact or associate with other molecules • We consider two cases: distinguishable and indistinguishable Distinguishable Particles • Particles that can be differentiated from each other • The particles could be in some way labeled (e. g. red vs. blue) or kept at a fixed position (e. g. particles in a crystal lattice) Indistinguishable Particles • Particles that cannot be differentiated from each other • These particles can interchange locations, so you cannot tell which particle is which (e. g. gas particles)

Partition Functions for Independent Particles Model System • Consider a system with energy levels Ej • The system consists of two independent subsystems with energy levels ei and em Distinguishable Particles • Label the two systems A and B • The system energy is • Where, i = 1, 2, …, a and m = 1, 2, …, b • The partition function of each subsystem is and

Partition Functions for Independent Particles Distinguishable Particles • The partition function for the entire system is • Because the subsystems are independent and distinguishable by their labels, the sum over i levels of A has nothing to do with the sum over m levels of B • Therefore, the partition function can be factored • More generally, when we have N independent and distinguishable particles the partition function simplifies to

Partition Functions for Independent Particles Indistinguishable Particles • There are no labels A or B the particles from each other • The system energy is • Where, i = 1, 2, …, t 1 and m = 1, 2, …, t 2 • The system partition function is • The summation can no longer be separated • As a result of performing the full summation, you overcount by a factor of 2! • Therefore, for N indistinguishable particles, the partition function evaluates to

Ideal Gases Molecular Definition • For an ideal gas there are no intermolecular interactions, i. e. , F = 0 • The molecules are unaware of each other’s existence and behave independently – the state molecule j is in is completely unaffected by the state of the other molecules in the gas Molecular Energies • We write the total energy of each molecule as the sum of the translational (kinetic) and internal energies • The internal energies include rotational, vibrational, electronic, and nuclear energies

Ideal Gases Molecular Energies • The schematic below gives an indication of the relative spacing between energy levels for the various energies electronic vibrational rotational translational

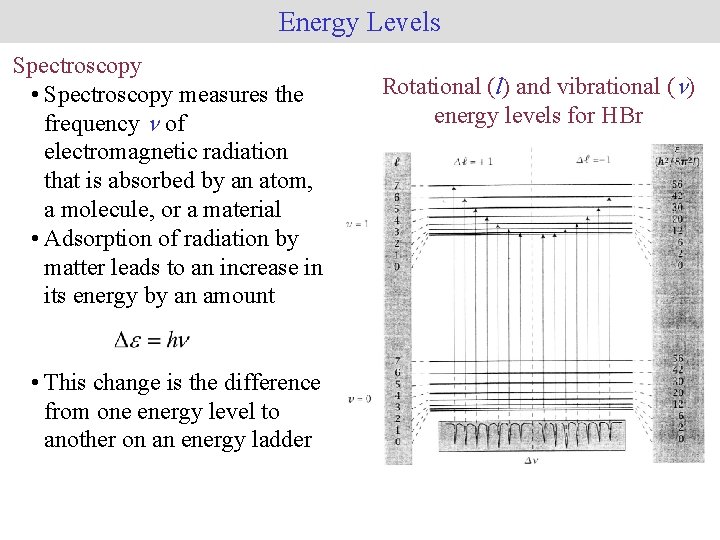
Energy Levels Spectroscopy • Spectroscopy measures the frequency n of electromagnetic radiation that is absorbed by an atom, a molecule, or a material • Adsorption of radiation by matter leads to an increase in its energy by an amount • This change is the difference from one energy level to another on an energy ladder Rotational (l) and vibrational (n) energy levels for HBr

Ideal Monatomic Gas • A monatomic gas has translational, electronic, and nuclear degrees of freedom • The translational Hamiltonian is separable from the electronic and nuclear degrees of freedom • The electronic and nuclear Hamiltonians are separable to a very good approximation • The molecular partition function can be written as • Each factor is treated independently – we now look at the various contributions

Energy Levels Quantum Mechanics • The basis for predicting quantum mechanical energy levels is the Schrödinger equation • The wavefunction y(x, y, z) is a function of spatial position • The square of this function, y 2, is the spatial probability distribution of the particles for the problem of interest • The Hamiltonian operator H describes the forces relevant for the problem of interest • In classical mechanics the Hamiltonian is given by the sum of kinetic and potential V energies • For example, for the one-dimensional translational motion of a particle having mass m and momentum p

Energy Levels Quantum Mechanics • While classical mechanics regards p and V as functions of time and spatial position, quantum mechanics regards p and V as mathematical operators that create the right differential equation for the problem at hand • In one dimension, the translational momentum operator is • Schrödinger’s equation is now • Only certain functions y(x) satisfy this equation • The quantities Ej are called eigenvalues and represent the discrete energy levels that we seek • The index j for the eigenvalues is called the quantum number

Translational Motion The Particle-in-a-Box Model • The particle-in-a-box is a model for the freedom of a particle to move within a confined space • A particle is free to move along the x-axis over the range 0 < x < L • At the walls (x = 0 and x = L) the potential is infinite (V(0) = V(L) = ∞) • Inside the box the molecule has free motion (V(x) = 0 for 0 < x < L) • Schrödinger’s equation is with • The solution to this differential equation is

Translational Motion The Particle-in-a-Box Model • The boundary conditions are and • Applying the boundary conditions and normalizing the probability distribution gives the following expressions for the wavefunction yn and energy en for a given quantum number n

Ideal Monatomic Gas Translational Partition Function • Quantum mechanics (particle in a box) tells us that the translational energy levels for a particle in a three-dimensional box are given by • The translational molecular partition function is now given by Example: For argon in a 1 cm 3 box,

Ideal Monatomic Gas Translational Partition Function • At most temperatures of practical importance, the energy levels are narrowly spaced in comparison to k. T • Therefore, we can replace the sum with an integral • which evaluates to • Using the de Broglie wavelength L, the result is with

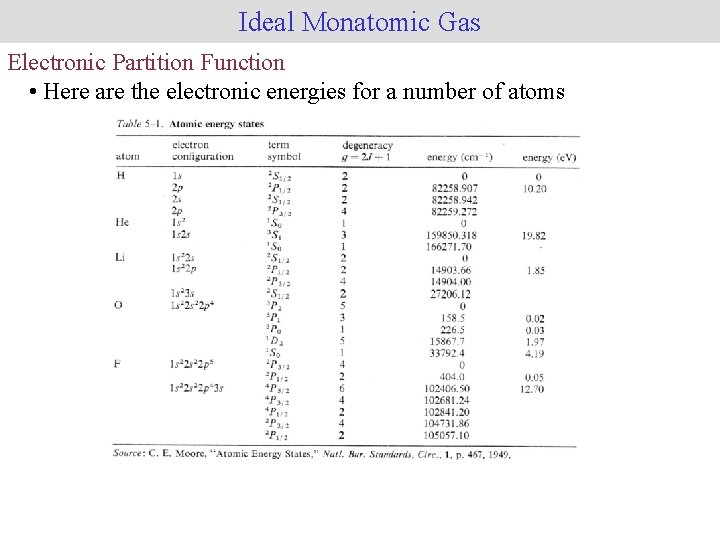
Ideal Monatomic Gas Electronic Partition Function • The electronic partition function is usually written as a sum over energy levels rather than a sum over states • Where wei and ei are the degeneracy and energy of the ith electronic level respectively • Generally, the first electronic level is set as the ground state (e 1 = 0) and the remaining energy levels are expressed in terms of their spacing relative to that of the ground state • Where De 1 j is the energy of the jth electronic level relative to the ground state • At ordinary temperatures, usually only the ground state and perhaps the first excited state need to be considered

Ideal Monatomic Gas Electronic Partition Function • Here are the electronic energies for a number of atoms

Ideal Monatomic Gas Example 1. What fraction of helium atoms are in their first excited state at T = 300 K and T = 3000 K 2. What fraction of fluorine atoms are in their first excited state at T = 200, 400, and 1000 K

Ideal Monatomic Gas Nuclear Partition Function • The nuclear partition function has a form similar to that of the electronic partition function • Nuclear energy levels are separated by millions of electron volts, which means temperatures on the order of 1010 K need to be reached before the first excited state becomes populated to any significant degree • Therefore, at ordinary temperatures we can simply express the nuclear partition function in terms of the degeneracy of the ground state • With this simplification the nuclear partition function only contributes to entropies and free energies

Ideal Diatomic Gas Overview • To a high degree of accuracy diatomic molecules can be described using the rigid rotor – harmonic oscillator approximation • With this approximation, in addition to the translational, electronic, and nuclear energies, the molecule has two additional energies • Rotational (rigid rotor): rotary motion about the center of mass • Vibrational (harmonic oscillator): relative vibratory motion of the two atoms • Again, we assume that all energies are independent, which gives the following expression for the molecular partition function

Ideal Diatomic Gas Energy levels • A quantum mechanical solution to the rigid rotor – harmonic oscillator problem gives the following energy levels and degeneracies for the rotational and vibrational motion Rigid Rotor I → moment of inertia re → bond length m → reduced mass → rotational const. Harmonic Oscillator v → frequency k → force constant → wave number

Ideal Diatomic Gas Ground State • Before obtaining the partition function, we need to set the ground state • We take the rotational ground state as the J = 0 state • For the vibrational energy, we have two choices q Take the lowest vibrational state to be the ground state q Take the bottom of the interatomic potential well as zero energy • We adopt the second choice • We take the zero of the electronic energy to be the separated, electronically unexcited atoms at rest • The electronic partition function is now

Ideal Diatomic Gas Vibrational Partition Function • With our choice of the ground state as the minimum in the interatomic potential well, the vibrational energies are given as • The partition function is given by a sum over all energy levels • This summation can be evaluated analytically

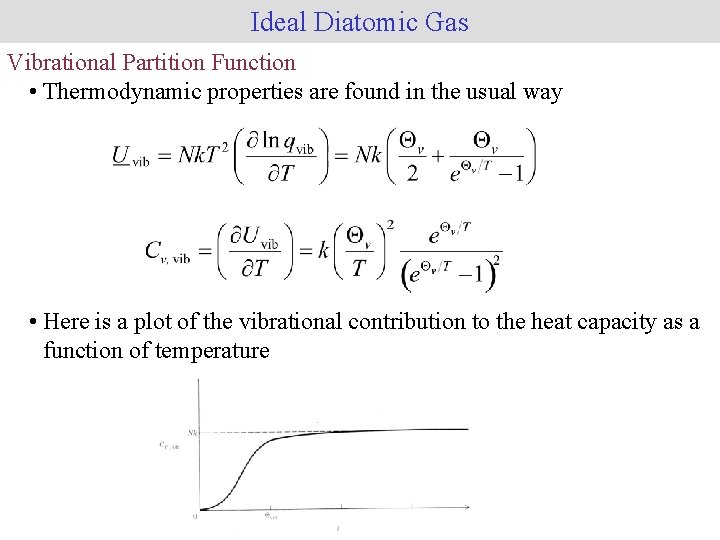
Ideal Diatomic Gas Vibrational Partition Function • Performing the summation gives the following exact solution • The vibrational temperature, Qv ≡ hv/k, is often used instead of the vibrational frequencies

Ideal Diatomic Gas Vibrational Partition Function • Thermodynamic properties are found in the usual way • Here is a plot of the vibrational contribution to the heat capacity as a function of temperature

Ideal Diatomic Gas Rotational Partition Function • The rotational energy levels are • The partition function is given by a sum over all energy levels • This summation cannot be written in closed form • At ordinary temperatures the energy levels are usually narrowly spaced compared to k. T and we can approximate the sum by an integral • Where we have introduced the rotational temperature

Ideal Diatomic Gas Rotational Partition Function • The integral evaluates to • This approximate solution is valid for temperatures that far exceed the characteristic temperature for rotation, i. e. , T >> Qr • Replacing the rotational temperature with the moment of inertia gives • As T approaches Qr the approximate solution is no longer valid and the actual summation must be performed

Ideal Diatomic Gas Rotational Partition Function • The approximate solution gives the following values for the energy and heat capacity

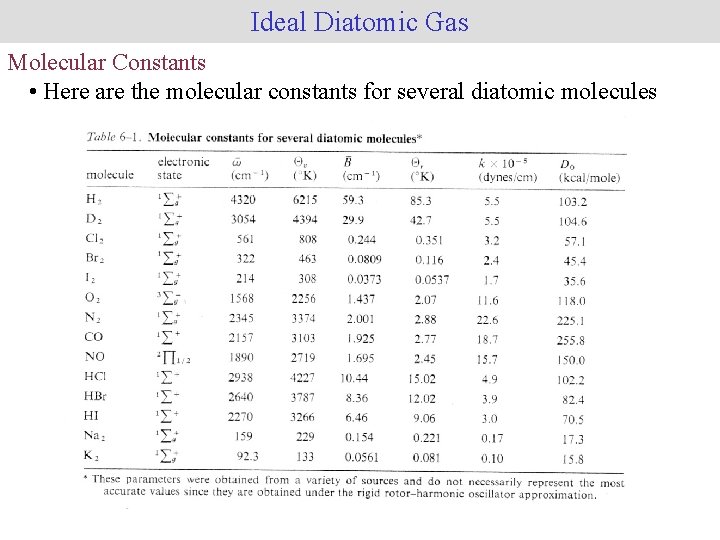
Ideal Diatomic Gas Molecular Constants • Here are the molecular constants for several diatomic molecules

Ideal Diatomic Gas Symmetry Number • The symmetry number (s) is a classical correction factor introduced to avoid over counting indistinguishable configurations • Its origin is quantum mechanical in nature and the approach presented here is appropriate at ordinary temperatures • The symmetry number represents the number of different ways a molecule can be rotated into a configuration indistinguishable from the original • By accounting for the symmetry of a molecule, the rotational partition function becomes

Ideal Diatomic Gas Symmetry Number • Here are the symmetry numbers for a number of common molecules Molecule Hydrogen Chloride Nitrogen Carbonyl Sulfide Carbon Dioxide Water Ammonia Methane Benzene Formula HCl N 2 COS s 1 2 1 CO 2 H 2 O NH 3 CH 4 C 6 H 6 2 2 3 12 12

Ideal Polyatomic Gas Overview • We now extend the methods we have developed for diatomic molecules to polyatomic systems • We use an analogous approach to that adopted previously for the translational, electronic, and nuclear energies • The vibrational partition function is a straightforward extension of the diatomic case • The rotational partition function is a bit more complicated, however a convenient solution exists as long as we can treat the molecule classically • A new feature that arises with polyatomic molecules is hindered (or internal) rotation (e. g. , rotation about the carbon-carbon bond in ethane) • The molecular partition function is

Ideal Polyatomic Gas Translational Partition Function • Once again, the translational partition function is expressed in terms of the de Broglie wavelength with • Where m is the molecular mass of the molecule Electronic Partition Function • Again, we choose as the zero of energy all n atoms completely separated in their ground electronic states • Therefore, the energy of the ground electronic state is –De • It follows that the electronic partition function is

Ideal Polyatomic Gas Vibrational Partition Function • The number of vibrational degrees of freedom a a molecule possesses is the difference between its total number of degrees of freedom (3 n) and the sum of the translational (3) and rotational (2 for linear and 3 for nonlinear molecules) degrees of freedom • A coordinate transformation can be completed such that a set of coordinates (normal coordinates) are found in which the Hamiltonian can be written in terms of a sum of a independent harmonic oscillators • The total vibrational energy is given by

Ideal Polyatomic Gas Vibrational Partition Function • Each of the vibrational modes can be treated independently and the vibrational partition function becomes • It follows that the internal energy and heat capacity are given as

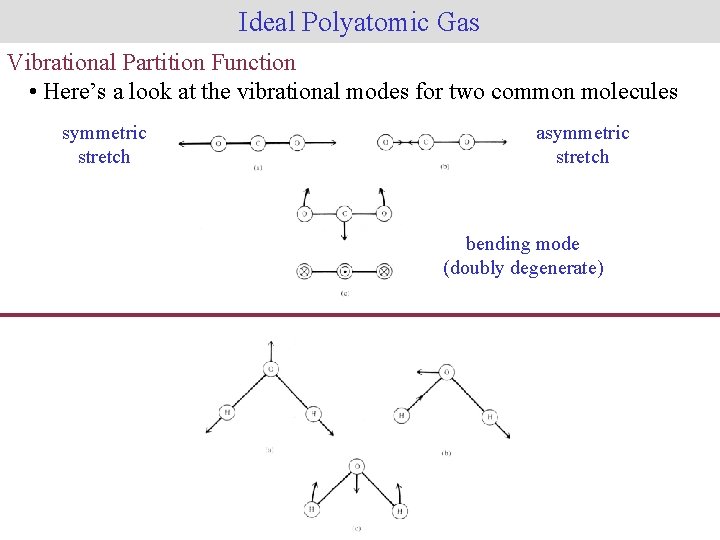
Ideal Polyatomic Gas Vibrational Partition Function • Here’s a look at the vibrational modes for two common molecules symmetric stretch asymmetric stretch bending mode (doubly degenerate)

Ideal Polyatomic Gas Rotational Partition Function (Linear Molecules) • For linear molecules, the quantum states are the same as for a diatomic molecule • Using the classical approximation the partition function is given by

Ideal Polyatomic Gas Rotational Partition Function (Nonlinear Molecules) • We describe the geometry of a nonlinear molecule in terms of its principal moments of inertia • These values are found with respect to a molecules principal axes, set such that all products of inertia are zero • The principal moments of inertia are usually denoted as follows • The three principal moments of inertia are used to define the corresponding rotational temperatures QA, QB, and QC

Ideal Polyatomic Gas Rotational Partition Function (Nonlinear Molecules) • The quantum mechanical energy levels depend on the relative values of the principal moments of inertia • Three cases exist: Spherical Top: IA = I B = I C Symmetric Top: IA = I B ≠ IC Asymmetric Top: IA ≠ I B ≠ IC A closed form solution does not exist

Ideal Polyatomic Gas Rotational Partition Function (Nonlinear Molecules) • If T is close to QA, QB, or QC, then the actual summations must be performed to obtain the partition function (the asymmetric top case requires a numerical solution) • In the classical limit T >> Q a general solution for the rotational partition function can be obtained • Simple relationships result for the internal energy and heat capacity

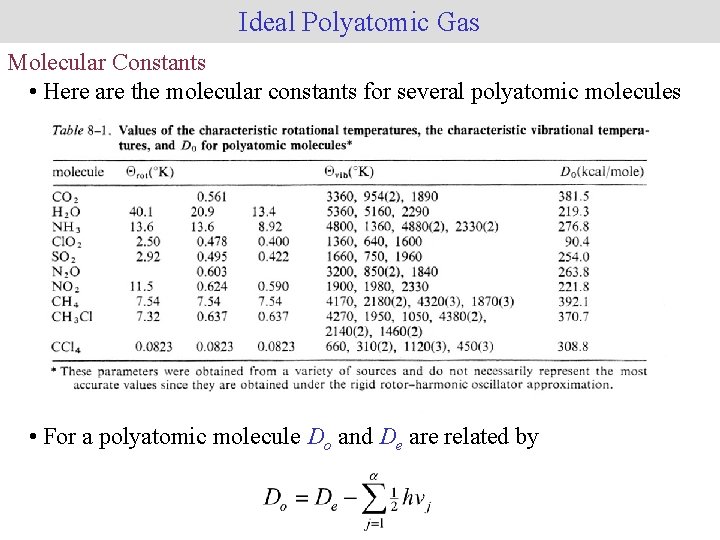
Ideal Polyatomic Gas Molecular Constants • Here are the molecular constants for several polyatomic molecules • For a polyatomic molecule Do and De are related by

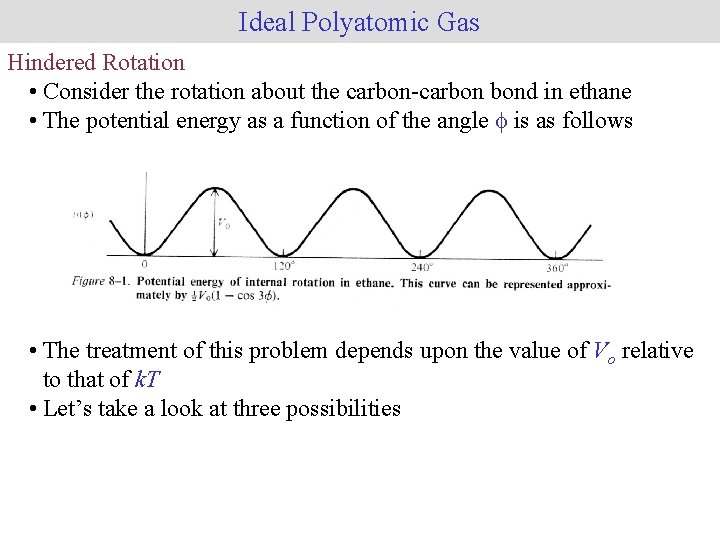
Ideal Polyatomic Gas Hindered Rotation • Consider the rotation about the carbon-carbon bond in ethane • The potential energy as a function of the angle f is as follows • The treatment of this problem depends upon the value of Vo relative to that of k. T • Let’s take a look at three possibilities

Ideal Polyatomic Gas Hindered Rotation • k. T >> Vo: in this case the internal rotation is essentially free and can be treated by methods similar to that for the rigid rotor • k. T << Vo: in this case the molecule is trapped at the bottom of the wells and the motion is that of a simple torsional vibration, which can be treated by a method similar to that used for the simple harmonic oscillator • k. T ≈ Vo: in this case neither of the above approximations is valid and the full quantum mechanical problem must be solved – the solutions have been tabulated for many common molecules • Unfortunately, for many molecules of practical significance, the latter case is found