Particles Waves What is Light part 2 Interference

Particles & Waves What is Light? (part 2): Interference

What is light? �Early scientists argued over the nature of light. �Was it composed of particles? �Was it a continuous wave? Newton (1700) –Particles (a guess) Thomas Young (1800) – a continuous wave (Double Slit experiment) Max Planck (1900) – particles (Photoelectric effect) Modern day idea : both (depending how you observe it!) This leads light to be considered to have: Wave Particle duality

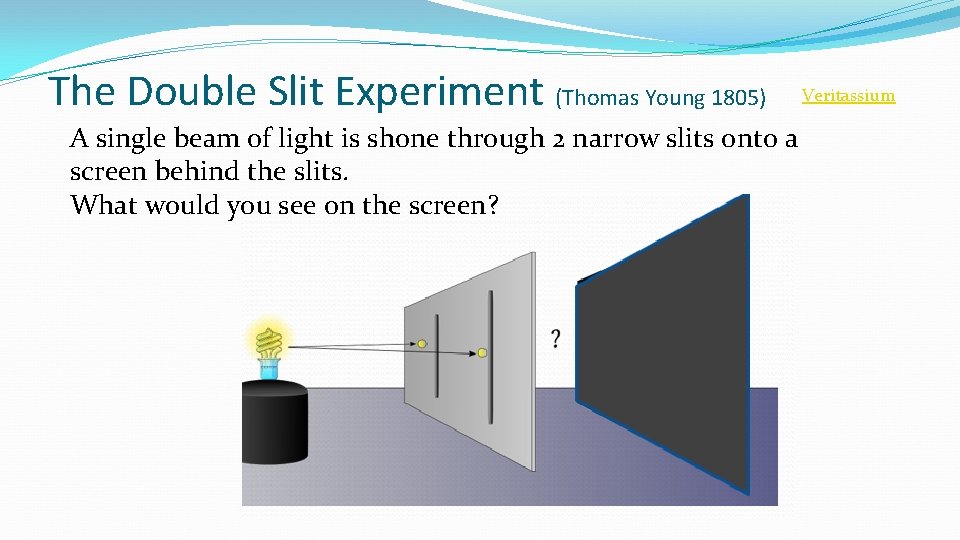
The Double Slit Experiment (Thomas Young 1805) A single beam of light is shone through 2 narrow slits onto a screen behind the slits. What would you see on the screen? Veritassium

Young’s double slit experiment �When the slits are very narrow and very close together (less than a millimetre), the following pattern is seen… Thomas Young used an orange sodium light source that only gave out one colour of light monochromatic light A series of bright and dark regions is observed. Thomas Young realised that the only way to explain this was to consider that light travelled as a continuous wave and that the light waves going through each slit were interfering with each other to produce an observable interference pattern

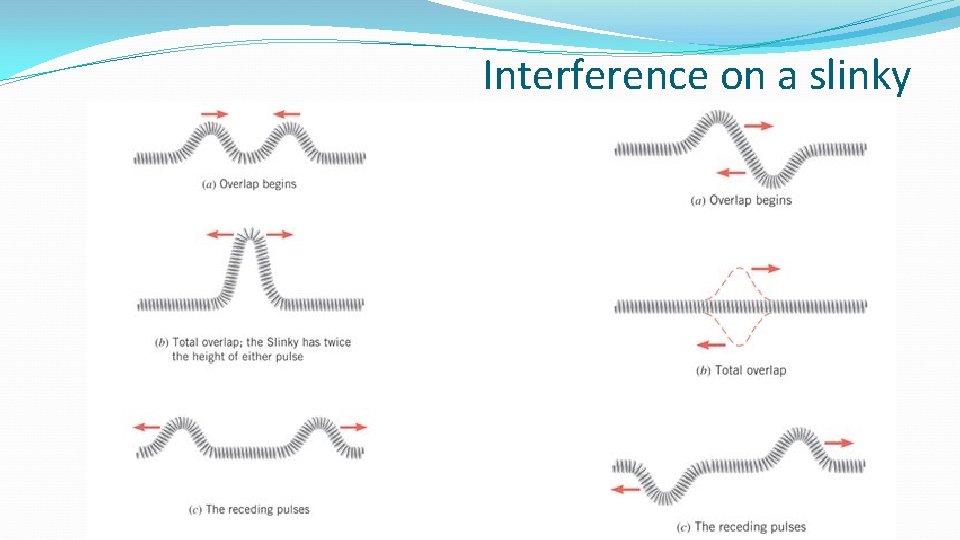
Interference on a slinky

Interference of sound waves Set up 2 loudspeakers 1 m apart emitting the same frequency of sound waves. (about 1000 Hz) The speakers are emitting coherent waves…. . they have the same frequency, wavelength and are in phase. Walk past them (about 3 m away) and you should detect louder and quieter regions as the sound waves interfere with each other !

Try this………. �On a sheet of plain paper……. . �Mark 2 points 10 cm apart on the left hand side �With a set of compasses draw concentric half circles from each point increasing by 1 cm each time. These are coherent ripples �Draw as many as you can from each point �Mark each point where the waves intersect with a small circle.

Explaining the pattern • Waves from a single light source pass through both narrow slits and form semi-circular waves. (by diffraction ) • These coherent waves interfere with each other. • When a crest meets a crest a maximum amplitude is produced. This is called constructive interference • When a crest meets a trough a minimum (or zero) amplitude is produced. This is called destructive interference. These regions of constructive and destructive interference produce the interference pattern

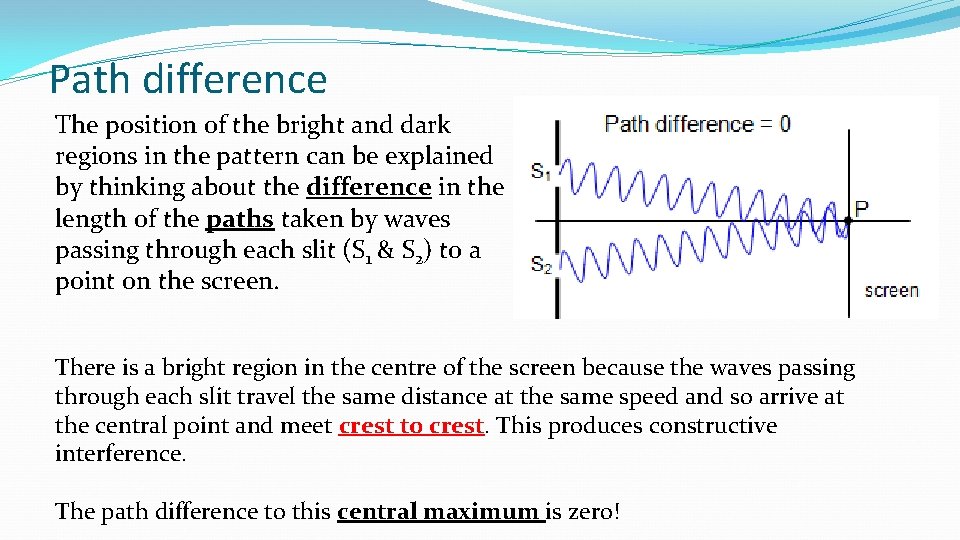
Path difference The position of the bright and dark regions in the pattern can be explained by thinking about the difference in the length of the paths taken by waves passing through each slit (S 1 & S 2) to a point on the screen. There is a bright region in the centre of the screen because the waves passing through each slit travel the same distance at the same speed and so arrive at the central point and meet crest to crest. This produces constructive interference. The path difference to this central maximum is zero!

Other bright regions…(maxima) �The other bright regions in the pattern on the screen must also be constructive interference too…. . a crest meets a crest at those points. �The only way this can happen is if the path difference is equal to a whole number of wavelengths The path difference to the first bright spot out from the middle is equal to 1 whole wavelength. The path difference to the 2 nd maximum = 2λ The path difference to the mth maximum = mλ (where m = 0, 1, 2, 3…)

What about the dark regions? (minima) Dark region corresponds to positions where the waves meet out of phase i. e. crest to trough. This produces destructive interference. The path difference to the first dark region (minimum) from the middle must be half a wavelength The path difference to the mth minimum = (where m = 0, 1, 2, 3…. . ) A little bit of geometry can be used to allow us to determine the wavelength of the light!

Deriving the equation: If point P is the first maximum out from the centre then the path difference S 2 P – S 1 P= λ Looking at the yellow right angle triangle…. . d = separation of the slits λ = wavelength of the light θ = the same as the angle between the central maximum and the first fringe at point P. λ (measured from the midpoint of the 2 slits) Therefore: So for any bright region : (where m is the number of the fringe) (This derivation is Not examinable!!)

Using the equation This equation can be used to determine the wavelength of monochromatic light from it’s interference pattern produced with a grating. We will use it to determine the wavelength of light from a red laser. All we need to measure is: D = distance to the wall x = distance from central max to the mth bright fringe d = the separation of the slits on the grating Using D and x we can calculate θ and then use A grating has multiple slits that gives a brighter pattern. Slit separation = 1/number of lines per metre to calculate the wavelength of the laser light.

Measuring the wavelength of a laser Results: �Distance to the wall = 1 m �Distance from central max to 1 st order fringe = 19. 4 cm �Separation of the slits = 3. 33 x 10 -6 m (300 lines per mm) Therefore wavelength of the laser = 634 nm (check it on the laser!) (School laser = 632. 8 nm)

Changing the slit separation �A small slit separation gives a wider interference pattern for the same light source (λ): as ‘d’ decreases, θ must increase. �A larger slit separation (or fewer lines per mm) gives a pattern where the fringes are closer together for the same light source(λ): as ‘d’ is increased θ must decrease. (This is why an interference pattern is only seen with narrow slits less than a millimetre apart. Slit separations of more than 1 mm do not produce an observable interference pattern)

Interference of white light The central maximum is white All wavelengths interfere constructively at this point. Every other maximum is a spectrum. Violet is closest to the central maximum in every spectrum. Since Violet has a smaller wavelength than red so the angle θ is smaller for violet than red in every spectrum (veritassium)

Summary �Light waves can interfere and an interference pattern can be produced. �Interference is a property of Waves! �Light must be behaving like a wave. �The grating equation allows the wavelength of light to be calculated from an interference pattern. �The wavelength of light is very small �Red is approx. 700 nm blue =approx. 450 nm