Particle Simulations Benjamin Glasser Particle Simulations Overview Physics

Particle Simulations Benjamin Glasser Particle Simulations

Overview • Physics of a collision – Experimental perspective • Instantaneous collisions • Sustained contacts http: //www. ux 1. eiu. edu/~cfadd/1150/ 07 Mom/Images/Newt. Pend. gif • Particle Simulations – Hard particle models • Event-driven – Soft particle models • Time stepping • Continuum models http: //www. ux 1. eiu. edu/~cfadd/11 50/07 Mom/Images/boing. gif Particle Simulations 2

Why? • To better understand, control, and optimize – Fluidization processes • Fluid bed reactors • Catalyst manufacture – Solids handling operations • Powder mixing • Hopper flow – Geophysical flows http: //www. rrdc. com/images/p h_peru_rockslide_lrg. jpg • Avalanches • Mudslides – Geophysical formations • Sand dunes • Martian topography Particle Simulations http: //photojournal. jpl. nasa. gov/jpeg. Mod/PIA 02405_mo dest. jpg 3

History • Leonardo da Vinci (1452 -1519) – first to device a simple and convincing experiment demonstrating dry friction. • Charles de Coulomb (1736 -1806) – Coulomb laws of dry friction between solids – would be extended to granular materials. • Michael Faraday (1791 -1872) – examined how vibrations affect sand piles. • William Rankine (1820 -1872) – examined friction in granular materials. • H. Jannsen (1880’s) – model of stresses in silos (granular material in a cylinder) • Lord Rayleigh (1842 -1919) – further work on stresses in containers • Osborne Reynolds (1842 -1912) – dilatency – expansion of material during shear • Ralph Bagnold (1950’s) – sand dunes, role of particle-particle interactions vs. fluid-particle interactions Particle Simulations 4

Benefits • • Ability to see “inside” granular flows Relatively cheap Permit theoretical investigations Investigate transitions between fluid-like and solid-like behavior Safer to run computer simulations Validate granular experiments Trace every particle http: //www. nature. com/n – Part of a force chain? • Versatility to be used for similar systems • Quick answers ature/journal/v 435/n 7045 /images/4351041 af 1. 2. jpg – Industry pleasing • Manipulate parameters – Coefficient of restitution – Coefficient of friction Poschel and Scwager. Computational Granular Dynamics. Springer, New York, 2005. Particle Simulations 5

A Simple Scenario Two particles approach one another with known initial velocity in a frontal (normal) impact Before: m 1 v 2 Conservation of momentum! 2 unknowns (u 1 and u 2) Require another equation Particle Simulations m 2 After: m 1 m 2 u 1 u 2 W. Goldsmith, Impact: Theory of Physical Behavior of Colliding Solids, 1960 6

A Simple Scenario If kinetic energy were conserved (elastic spheres): Then: and However, energy is not conserved inelastic collisions Particle Simulations 7

Inelastic Collisions • Initial velocity is v, rebound velocity is –ev • Unique to granular materials • Why? – Permanent deformation • Microcracks • Deformed surface – Acoustic Waves • Dissipated through heat Particle Simulations http: //www. mathworks. co m/access/helpdesk/help/te chdoc/math/ballode. gif 8

Coefficient of Normal Restitution • ε is the coefficient of normal restitution • • Ratio of pre-collisional to post-collisional velocities Source: Jacques Duran, Sands, Powders, and Grains, Springer, 1999. • Change in Kinetic Energy • Function of approaching velocity • Common values: Glass spheres 100 cm/s 0. 95 - 9 Steel spheres 100 cm/s 0. 91 - 0. 95 Brass spheres 100 cm/s 0. 9 Particle Simulations 9

Matrix Equations • Reference: System center of gravity – Particle - Particle Source: Jacques Duran, Sands, Powders, and Grains, Springer, 1999. – Particle – Wall (infinite mass, rigid body) u 0: velocity of wall u 1: particle velocity Particle Simulations 10

Normal Collision - No Friction § Only translational motion § x and y are components of linear momentum • ux = -evx • • u y = vy • 1 = 0 w 1 y x Particle Simulations 11

Spin and Friction § Spherical, Spinning Ball - Vertical Wall § Precollisional velocities § Compute: • vx • vy • w 0 • ux • uy • w 1 w 0 w 1 y y x x Particle Simulations 12

Normal Collision - Friction m: coefficient of friction between the ball and the wall Can distinguish between two cases based on m Case I: Source: Jacques Duran, Sands, Powders, and Grains, Springer, 1999. § Gliding velocity remains positive and non-zero w 1 y x Coulomb Rotation a: radius § True when: 4 Equations, 4 Unknowns (X, ux, uy, w 1) Particle Simulations 13

Normal Collision - Friction Case II: § Gliding velocity drops to 0 during the collision w 1 y x Rotation Pure rotation Particle Simulations True when: 14

Non-Frontal Collision with Friction v 2 w 2 • Two particles w 1 – Diameter d 1 and d 2 – Mass m 1 and m 2 – Unit vector normal to contact 1 n 2 v 1 • – Relative velocity at point of contact • Relative linear velocity Contribution from spin Particle Simulations The magnitude of the relative velocity |vc| increases when the individual velocities point in opposite directions and when the rotations are in the same direction 15

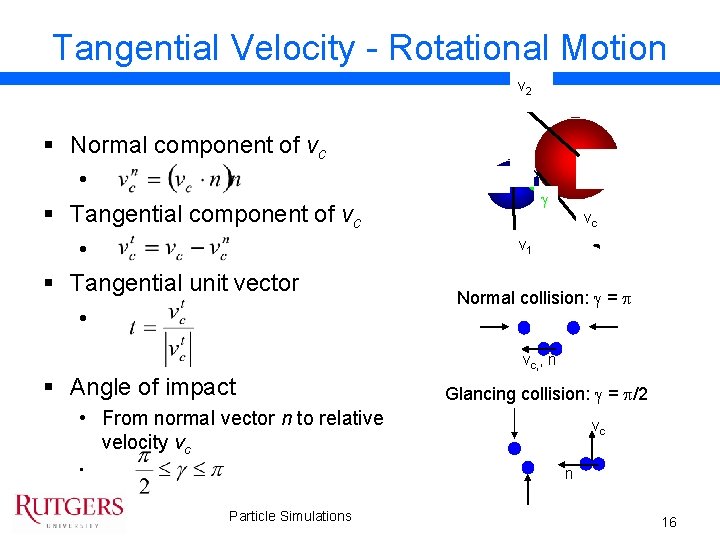
Tangential Velocity - Rotational Motion v 2 § Normal component of vc • § Tangential unit vector • 1 2 n g vc v 1 Normal collision: g = p vc, , n § Angle of impact Glancing collision: g = p/2 • From normal vector n to relative velocity vc • vc n Particle Simulations 16

Momentum Change • Linear change of momentum from a collision • Tangential contribution to angular momentum (torque) – Normal component of DP has no contribution for i=1, 2 – Ii: moment of inertia of particle i – The change in angular momentum is the same for both particles Particle Simulations 17

Outcome of the Collision Making use of the equations, one can compute the outcome of the collision Linear Velocity Where: DP = DPt + DPn The translation velocities before and after the collision are still related by this Angular Velocity Particle Simulations 18

Rolling • The previous equations describe all collisions on the basis of Coulomb’s Law (m) and e and nothing else • Ignored an important physical mechanism: rolling – Heuristic model to agree with experiments w 1 w 2 – Fire two spheres together with initial spin and examine the outcomes – Coefficient of tangential restitution, b • Equal to the smallest of two values: • b 0 – Rolling; b 1 – Sliding/Gliding Particle Simulations 19

Critical Angle – g 0 Applies for this form of the momentum equation For g > g 0: Rolling regime For g < g 0: Sliding/Gliding regime Small values of g correspond to dry friction (previous result) S. F. Forrester et al. , Phys. Fluids, 6, p. 1108 (1994) Particle Simulations 20

Sustained Contacts Jacques Duran, Sands, Powders, What about particles that are not completely rigid? Source: and Grains, Springer, 1999. Spheres can deform Can have interpenetration of the spheres, resulting in long contact times Consider 2 identical spheres – Mass, M – Radius, R R R relative velocity v x Hertz’s elastic energy Stored by each sphere during contact where Fan and Zhu, Principles of Gas-Solid Flow, 1998 E – Young’s modulus s – Poison’s ratio Ratio of transverse strain to longitudinal strain Particle Simulations 21

Sustained Contact Quantities • Upon impact the kinetic energy is converted into a reduced kinetic energy and stored elastic energy – Energy balance: • Velocity drops to zero when the two spheres have overlapped by a distance 0 • The entire duration of the collision (up to x 0 and recoil) Important: t only depends weakly on v – exponent is 1/5. Thus the duration of impact is only a weak function of the initial relative velocity Particle Simulations 22

Example Calculation Consider aluminum beads (r = 2. 70 g/cc) 1. 5 mm in diameter moving towards one another at 5 cm/s. E = 6 x 1011 dynes/cm 2 D=1. 5 mm s = 0. 3 What is the duration of contact? Answer: k = 7 x 1010 dynes/cm 3/2 m = 4. 77 x 10 -3 g t = 1. 15 x 10 -5 s Particle Simulations 23

Issues • Exceed elasticity limit – Plastic, not elastic deformations – Model can be adjusted to handle this • Energy dissipation – Sound waves – Heat • Spin complications – Can handle similar to rigid spheres Particle Simulations 24

Particle Simulations • Follow trajectories of individual particles – Incorporate statics and dynamics • Methods Source: Jacques Duran, Sands, Powders, and Grains, Springer, 1999. – Particle dynamics Source: Thorsten Poschel, Thomas Schwager, Computational Granular Dynamics, Springer, 2005. • Hard Particles • Soft Particles – Cellular automata Baxter and Behringer (1990) Cellular Automata of Granular Flows. Phys. Review A. , 42, 1017 -1020 • Motion evolves according to simple rules based on lattice sites – Monte-Carlo Rosato et al. (1987) Monte Carlo simulation of particulate matter segregation. Powder Technology, 49, 59 -69 • Analogous to molecules but change probabilities to match particles • Assumption of molecular chaos Particle Simulations 25

Boundary Conditions • Wall constructed from individual particles • Containers do not follow Newton’s equation of motion – Predetermined path as a function of time • Vibrated bed • Moving plate • Rotating vessel • Periodic boundaries – Can mimic infinitely-wide regions Particle Simulations 26

Initial Conditions • Depending on the algorithm (predictorcorrector), you may need to define higher order derivatives • Most long-term behavior is independent of initial conditions • Often, random (non-overlapping) positions and velocities are assigned Particle Simulations 27

Hard Particles • Event Driven (ED) • Strictly binary collisions • No integration of the equations of motion – More efficient Without gravity v 10 With gravity v 20 Collision at (xc, yc) Collision at (xc, yc + 1/2 gt 2) • Without gravity – straight line paths • With gravity – parabolas • Time to collision is identical Particle Simulations 28

Particle Motion • Consider a particle – Position vector xi – Velocity vector vi – Initial position (t=0) • xi = xi 0 • vi = vi 0 y xi 0 = (x, y) vi 0 = (vx, vy) di x – Undeterred position at time t Particle Simulations 29

Collision Prediction Two particles collide if: j di/2 dj/2 i Insert the equation of motion: (same force on each particle, so the accelerations are equal as well and cancel) Expand : Real root > 0 Particle Simulations collision 30

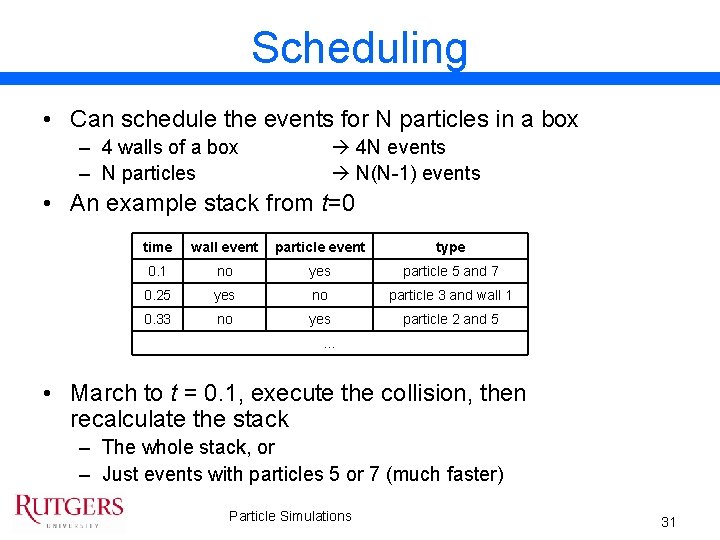
Scheduling • Can schedule the events for N particles in a box – 4 walls of a box – N particles 4 N events N(N-1) events • An example stack from t=0 time wall event particle event type 0. 1 no yes particle 5 and 7 0. 25 yes no particle 3 and wall 1 0. 33 no yes particle 2 and 5 … • March to t = 0. 1, execute the collision, then recalculate the stack – The whole stack, or – Just events with particles 5 or 7 (much faster) Particle Simulations 31

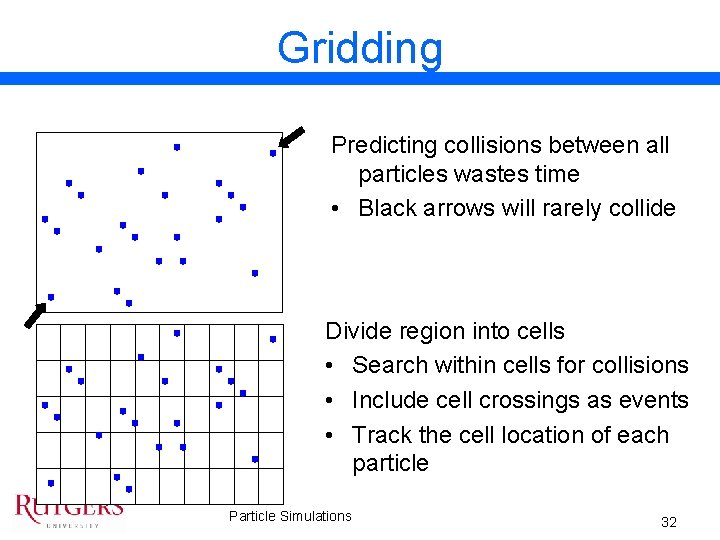
Gridding Predicting collisions between all particles wastes time • Black arrows will rarely collide Divide region into cells • Search within cells for collisions • Include cell crossings as events • Track the cell location of each particle Particle Simulations 32

Inelastic collapse Left and right particle collide with the middle particles alternately until the motion of all three particles is zero Poschel and Scwager. Computational Granular Dynamics. Springer, New York, 2005. Only for a constant coefficient of restitution – Not valid for real materials – Experiments suggest e is a function of v Particle Simulations 33

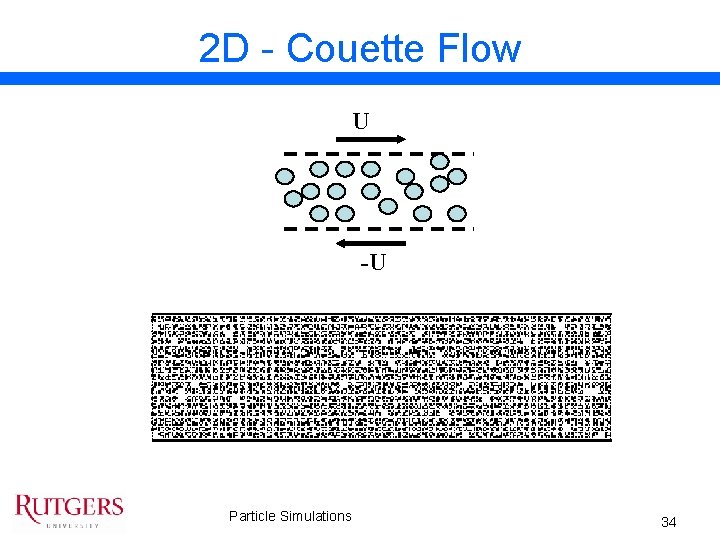
2 D - Couette Flow U -U Particle Simulations 34

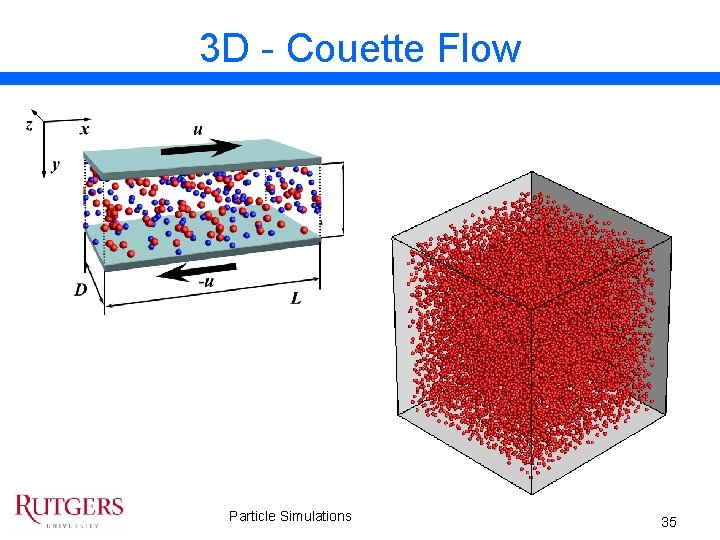
3 D - Couette Flow Particle Simulations 35

Soft Particles • • Force-based Time stepping Small overlap allowed Useful for x – Statics – Dense quasi-static flows • To follow particles: F is the normal force on particles proportional to amount of overlap Particle Simulations 36

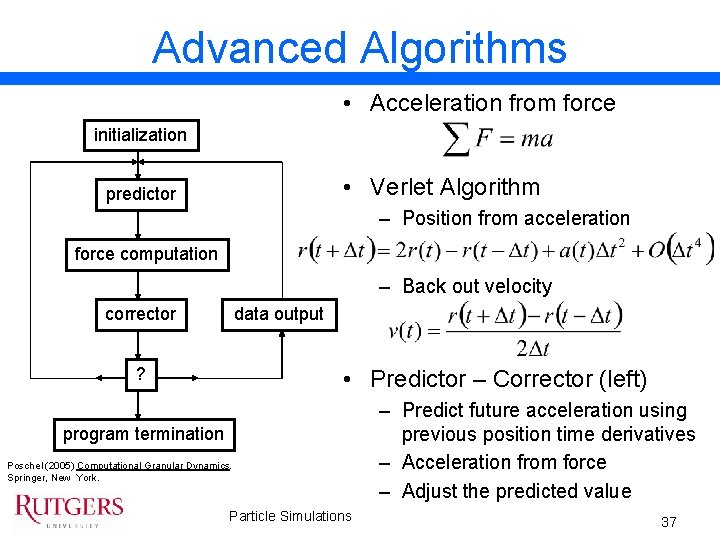
Advanced Algorithms • Acceleration from force initialization • Verlet Algorithm predictor – Position from acceleration force computation – Back out velocity corrector data output ? • Predictor – Corrector (left) program termination Poschel (2005) Computational Granular Dynamics. Springer, New York. Particle Simulations – Predict future acceleration using previous position time derivatives – Acceleration from force – Adjust the predicted value 37

Contact Models • Spring and Dashpot – e may be related to kn and gn Poschel (2005) Computational Granular Dynamics. Springer, New York. • Mutual compression of particles i and j Particle Simulations 38

Force Calculation • In addition to Fn – Gravity – Wall forces – Interstitial fluid – Spin – Cohesion F 2 Fw F 3 Fg Total of all is the resultant force on the particle, F Particle Simulations 39

More Contact Models Hertz Kuwabara and Kono Poschel (2005) Computational Granular Dynamics. Springer, New York. Walton and Braun (right) Can also include friction in the mechanism Particle Simulations 40

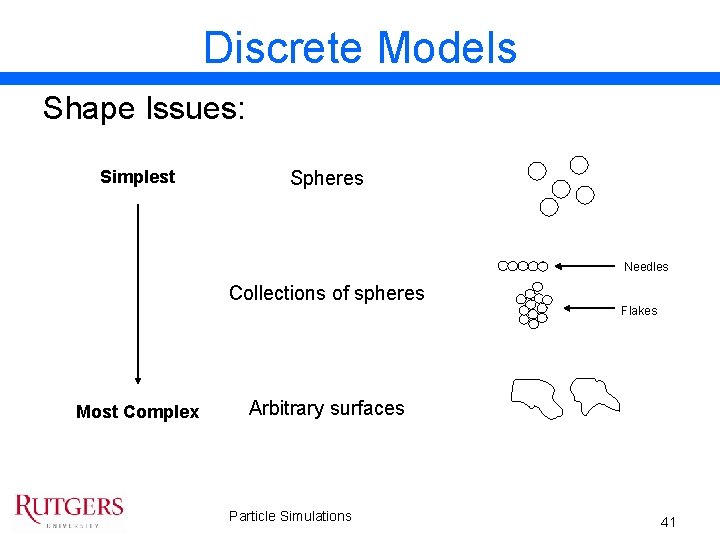
Discrete Models Shape Issues: Simplest Spheres Needles Collections of spheres Most Complex Flakes Arbitrary surfaces Particle Simulations 41

Results: Constant inter-particle force Model • Optimized Condition: 20, 000 particles, 2 mm diameter, in an axially smaller rotating drum of 9 cm radius and 1 cm length are considered. The sidewalls are made frictionless to avoid end wall effects. • Inter-particle or particle-wall cohesive force is varied such that K=4575 • Fast-Flo Lactose • Size: 100 micron Avalanches start appearing at K = 30 and become bigger at K =45. Distinct angles of repose are visible at top and bottom of “cascade” layer. RPM = 7 K = 45 ; RPM = 20 sp = 0. 8 ; dp = 0. 1 ; sw = 0. 5 dw = 0. 5 ; Credit: F. Muzzio Particle Simulations 42

Results: Constant inter-particle force Model Dynamic friction within the particles and the cohesion are increased to simulate the flow of more cohesive material. Wall friction is increased. K = 60 ; RPM = 20 Avicel-101; Size : 50 m; RPM = 7 sp = 0. 8 ; dp = 0. 6 ; sw = 0. 8 ; dw = 0. 8 K = 75 ; RPM = 20 Reg. Lactose; Size : 60 m; RPM = 7 sp = 0. 8 ; dp = 0. 6 ; sw = 0. 8 ; dw = 0. 8 Similarities: 8 Increase in size of avalanches. 8 Mixture of splashing and timid bulldozing. Particle Simulations 8 Mixture of chugging and bulldozing. 8 Periodic Avalanches 8 Bigger Avalanches Credit: F. Muzzio 43

Uniform Binary System Comparison of model and experiment • Optimized Condition: 10, 000 red and 10, 000 green particles of same size (radius: 1 mm) are loaded side by side along the axis of the drum. The drum of radius 9 cm and length of 1 cm is considered. The sidewalls are made frictionless to avoid wall effects. • Inter-particle or particle-wall cohesive force is varied such that K=0 – 120 Glass beads (40 m) K=0 Colored Avicel (50 m) K=60 RPM=10 RPM = 20 • No avalanches. • Mixes well in 3 -4 revolutions • Avalanches appearing • Slower mixing Credit: F. Muzzio Particle Simulations 44

Non-uniform Binary System Experiment: Blue (30 mm) and Red glass beads (50 mm) of equal mass are axially loaded side by side in a drum of radius = 7. 5 cm and length 30 cm. Simulation: 8000 blue particles (1 mm) and 2370 red particles(1. 5 mm) of same density are loaded side by side along the axis of the drum. Red and blue particles of are of the same total mass. RPM =12 RPM =20 Inter-particle Force Model FRR = KRR WB (red-red pair) FRB = KRB WB (red-blue pair) FBB = KBB WB (blue-blue pair) WB is the weight of a blue particle. Credit: F. Muzzio Particle Simulations Non-cohesive binary mixture : Axial Size Segregation is evident in both (K. M. Hill et. al Phys. the simulation and Rev. E. , 49, 1994). experiments. 45

Example –A Particle/Wall Contact 2 D Disk - Flat, Vertical Wall • • R kn Dt m v p 0 xw = 0. 5 mm = 10 N mm-3/2 = 0. 25 s = 0. 148 kg = (vx 0, vy 0) = (1 mm s-1, 0 mm s-1) = (xx 0, xy 0) = (1. 2 mm, 1 mm) = 0 (line from origin to +∞) y x Particle Simulations y x 46

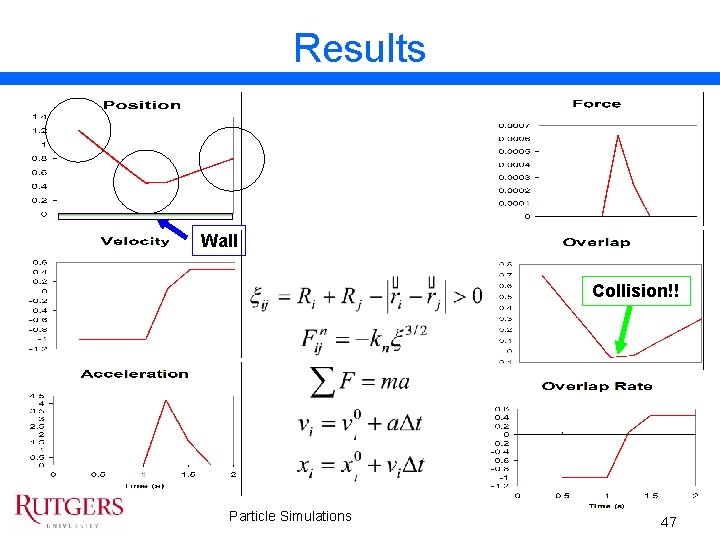
Results Wall Collision!! Particle Simulations 47

Hard vs. Soft • When to use hard (event) instead of soft (force) – Average collision duration << Time between collisions • Granular gases cosmic dust clouds – Unknown interaction force Poschel (2005) Computational Granular Dynamics. Springer, New York. • Non-linear materials • Complicated particle shapes • Can experimentally determine pre- and post-collisional velocities Particle Simulations 48

Drawbacks • Computationally expensive – Dt << t to calculate forces – 20, 000 particles • Real time of seconds to minutes • Dynamic issues – Strain hardening – Contact erosion over time Particle Simulations 49

Continuum • Discrete particles replaced (averaged out) with continuous medium • Quantities such as velocity and density are assumed to be smooth functions of position and time • Volume element (dv) contains multiple particles • Time (dt) should be large compared to time required for a particle to cross dv Truesdall, C. and Muncaster, R. G. (1980) – Fundamentals of Maxwell’s Kinetic Theory of a Simple Monatonic Gas. Academic Press, pp. xvi. Particle Simulations 50

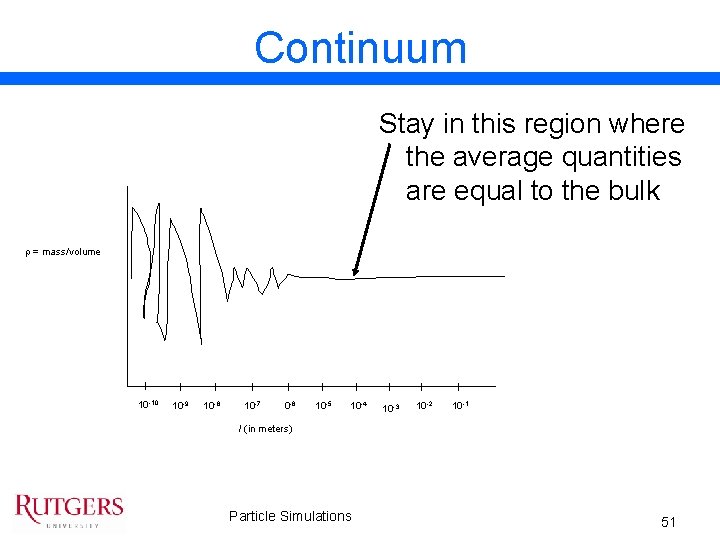
Continuum Stay in this region where the average quantities are equal to the bulk r = mass/volume 10 -10 10 -9 10 -8 10 -7 10 -6 10 -5 10 -4 10 -3 10 -2 10 -1 l (in meters) Particle Simulations 51

Continuum Simulation for Granular Flows Average over a small region in a granular flow. Consider a mass balance over a stationary volume element of size ΔxΔyΔz. Rate of mass accumulation = rate of mass in – rate of mass out Δz Granular Flow Dividing by ΔxΔyΔz and taking limits, we obtain Δx Δy or We can extend this approach to calculate momentum and energy balance. § Particle Dynamic Simulations – Limited by computational resources § Continuum Simulations with physically realistic closures (Use a set of equations for design, control and optimization) ð More efficient design, scaling & control through Continuum modeling Particle Simulations 52

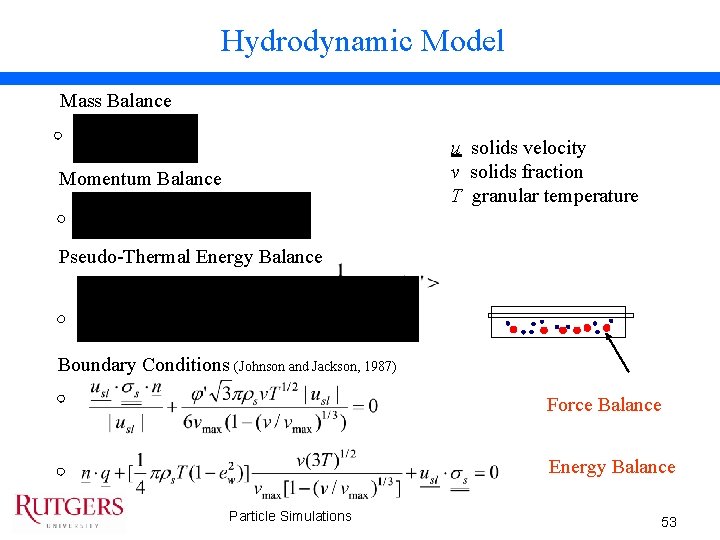
Hydrodynamic Model Mass Balance u solids velocity v solids fraction T granular temperature Momentum Balance Pseudo-Thermal Energy Balance Boundary Conditions (Johnson and Jackson, 1987) Force Balance Energy Balance Particle Simulations 53

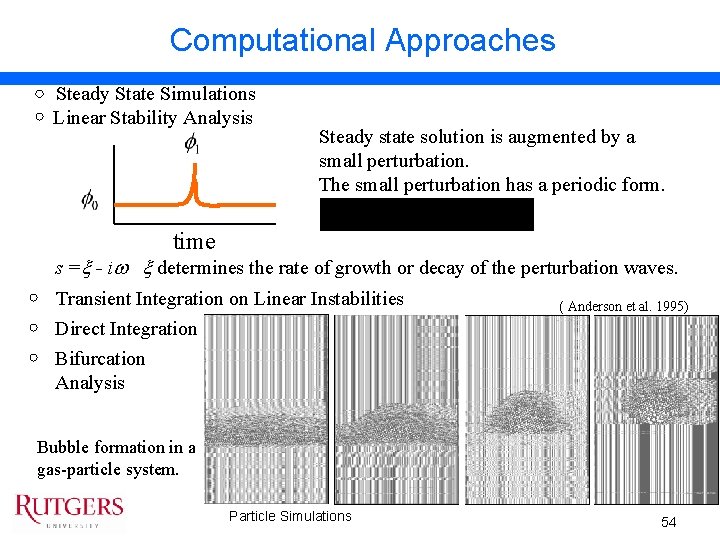
Computational Approaches Steady State Simulations Linear Stability Analysis Steady state solution is augmented by a small perturbation. The small perturbation has a periodic form. time s = - i determines the rate of growth or decay of the perturbation waves. Transient Integration on Linear Instabilities Direct Integration Bifurcation Analysis ( Anderson et al. 1995) Bubble formation in a gas-particle system. Particle Simulations 54

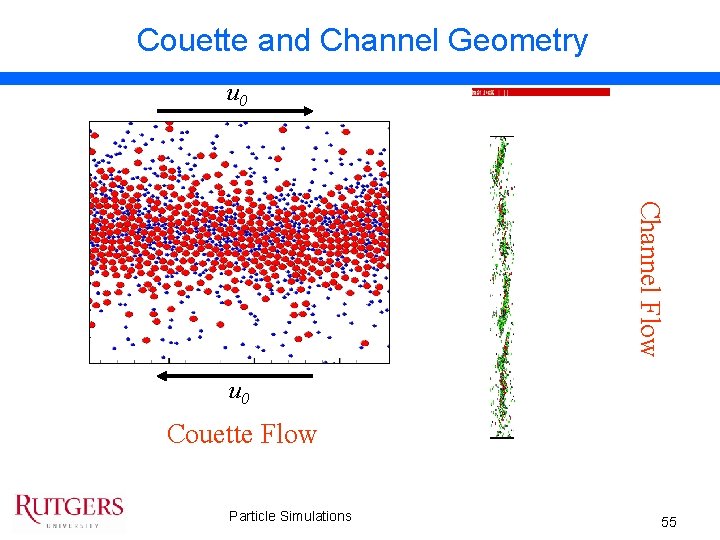
Couette and Channel Geometry u 0 Channel Flow u 0 Couette Flow Particle Simulations 55

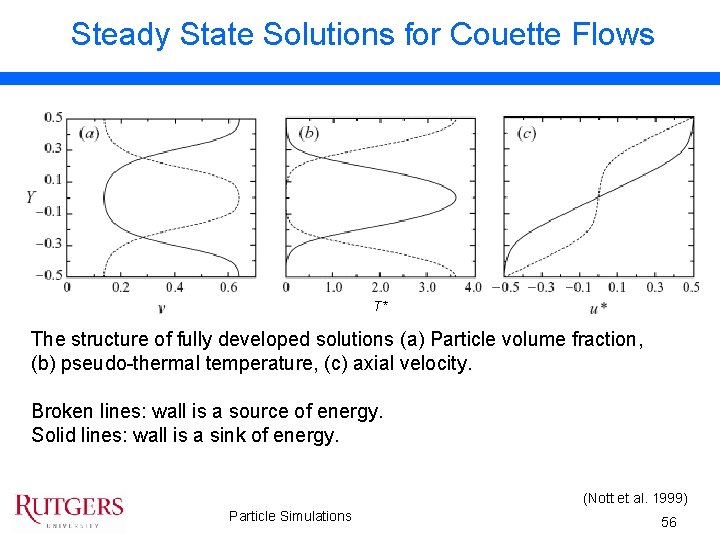
Steady State Solutions for Couette Flows T* The structure of fully developed solutions (a) Particle volume fraction, (b) pseudo-thermal temperature, (c) axial velocity. Broken lines: wall is a source of energy. Solid lines: wall is a sink of energy. (Nott et al. 1999) Particle Simulations 56

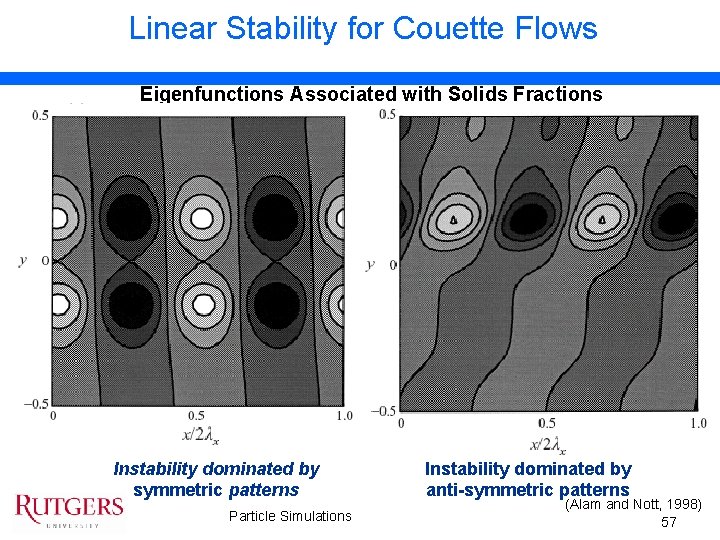
Linear Stability for Couette Flows Eigenfunctions Associated with Solids Fractions Instability dominated by symmetric patterns Particle Simulations Instability dominated by anti-symmetric patterns (Alam and Nott, 1998) 57

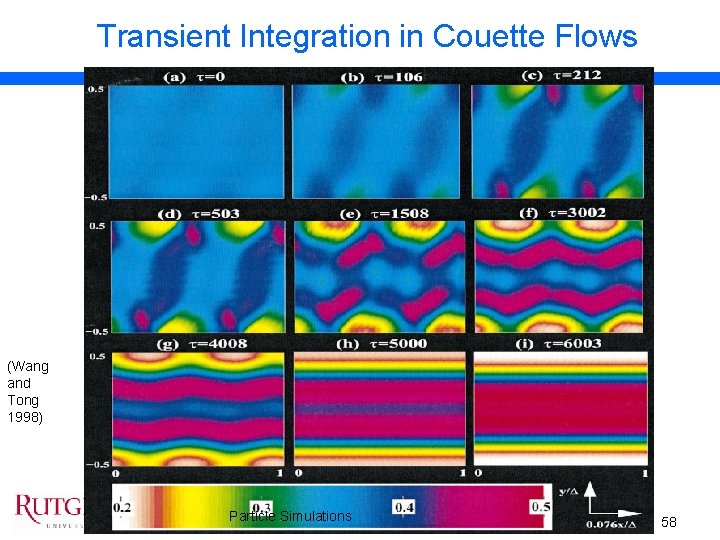
Transient Integration in Couette Flows (Wang and Tong 1998) Particle Simulations 58

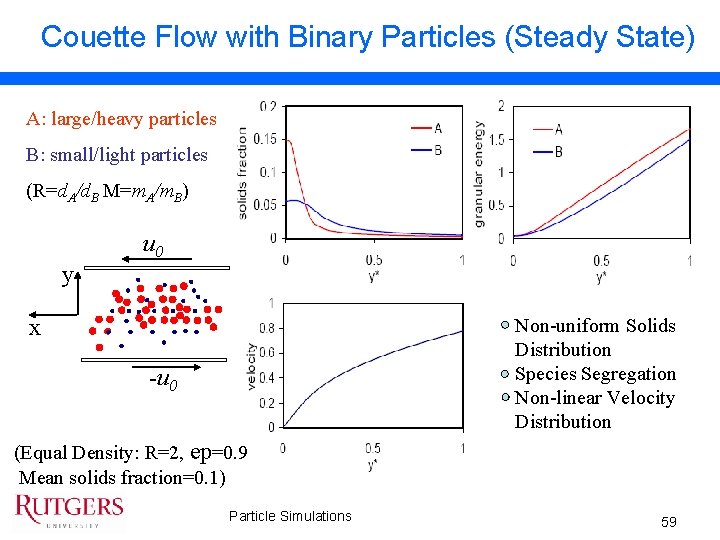
Couette Flow with Binary Particles (Steady State) A: large/heavy particles B: small/light particles (R=d. A/d. B M=m. A/m. B) y u 0 x Non-uniform Solids Distribution Species Segregation Non-linear Velocity Distribution -u 0 (Equal Density: R=2, ep=0. 9 Mean solids fraction=0. 1) Particle Simulations 59

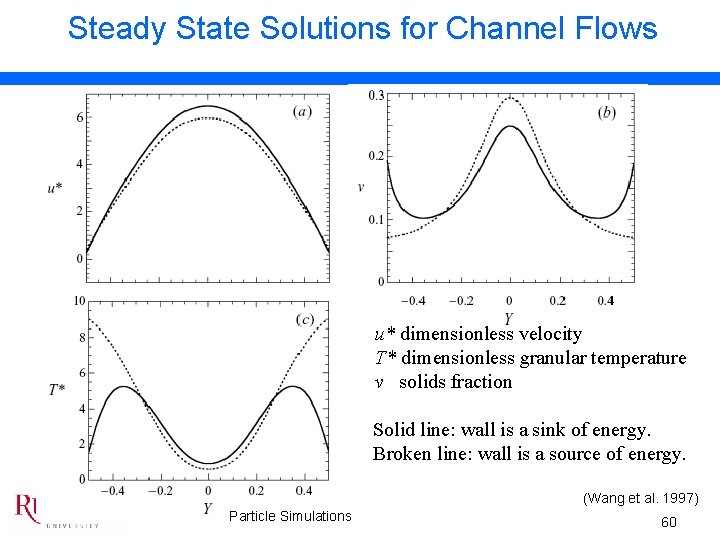
Steady State Solutions for Channel Flows u* dimensionless velocity T* dimensionless granular temperature v solids fraction Solid line: wall is a sink of energy. Broken line: wall is a source of energy. (Wang et al. 1997) Particle Simulations 60

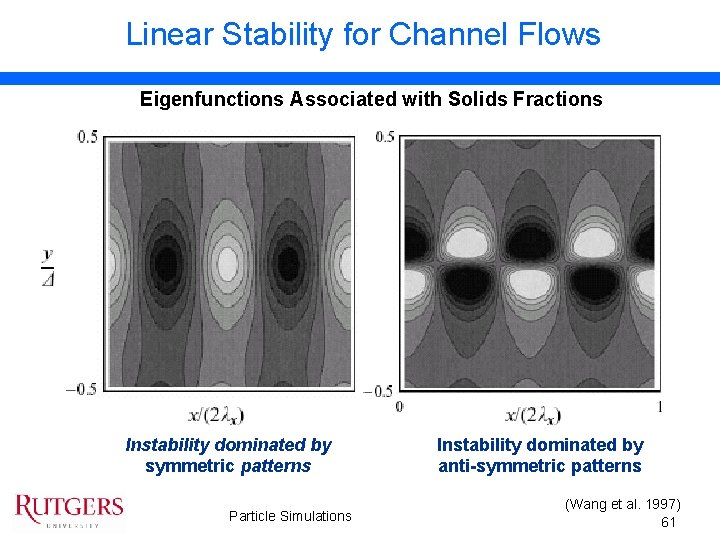
Linear Stability for Channel Flows Eigenfunctions Associated with Solids Fractions Instability dominated by symmetric patterns Particle Simulations Instability dominated by anti-symmetric patterns (Wang et al. 1997) 61

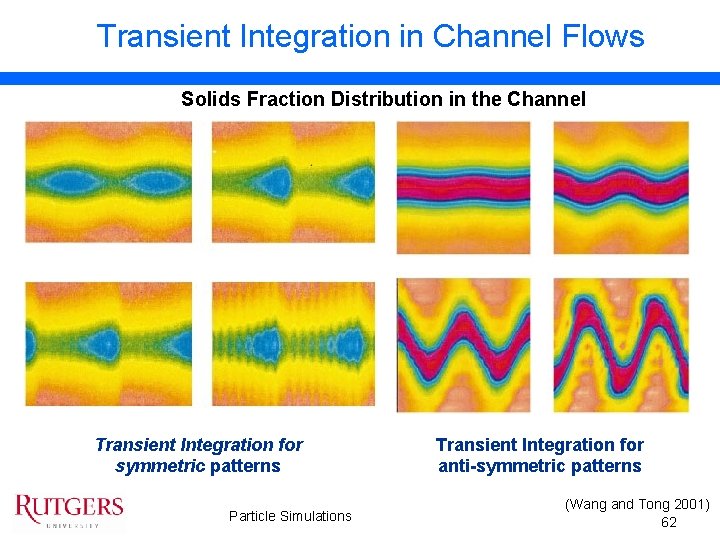
Transient Integration in Channel Flows Solids Fraction Distribution in the Channel Transient Integration for symmetric patterns Particle Simulations Transient Integration for anti-symmetric patterns (Wang and Tong 2001) 62

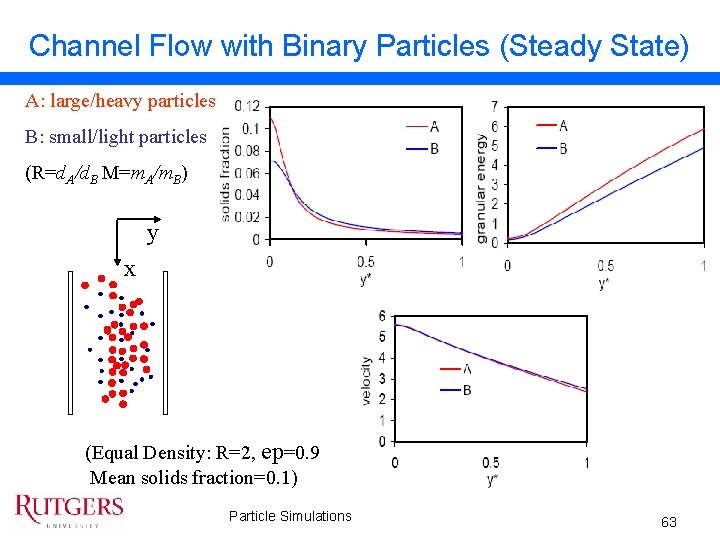
Channel Flow with Binary Particles (Steady State) A: large/heavy particles B: small/light particles (R=d. A/d. B M=m. A/m. B) y x (Equal Density: R=2, ep=0. 9 Mean solids fraction=0. 1) Particle Simulations 63