Particle physics precision precision and precision or three

Particle physics: precision, precision and precision… …or three decades without unexpected discoveries Mihail Chizhov Sofia University, Bulgaria

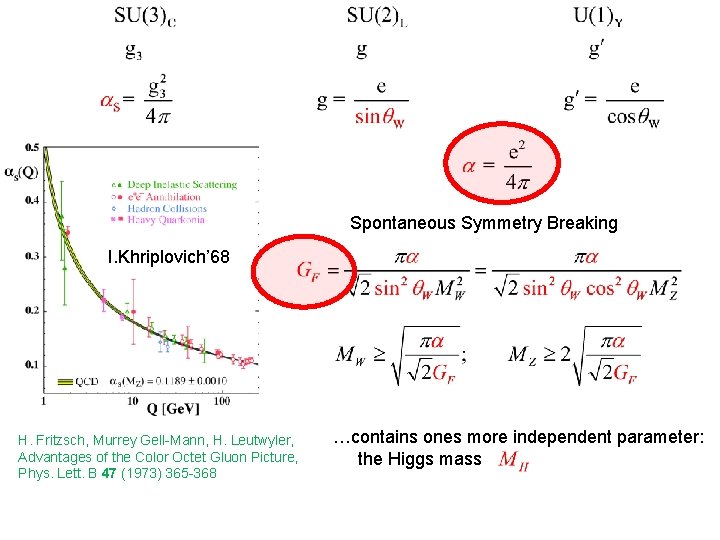
Spontaneous Symmetry Breaking I. Khriplovich’ 68 H. Fritzsch, Murrey Gell-Mann, H. Leutwyler, Advantages of the Color Octet Gluon Picture, Phys. Lett. B 47 (1973) 365 -368 …contains ones more independent parameter: the Higgs mass

T. Kinoshita & A. Sirlin, Phys. Rev. 113 (1959) 1652 T. van Ritbergen & R. G. Stuart, Phys. Rev. Lett. 82 (1999) 488 Theoretical uncertainty in the determination of GF is less than 0. 3 ppm, the final goal of Mu. Lan experiment is 0. 5 ppm.

Choosing the third constant

while direct W-boson mass measurements give Quantum corrections !!!

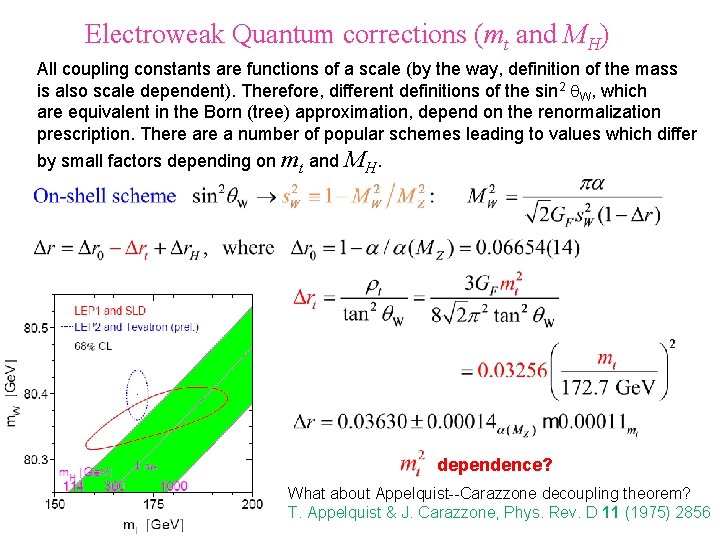
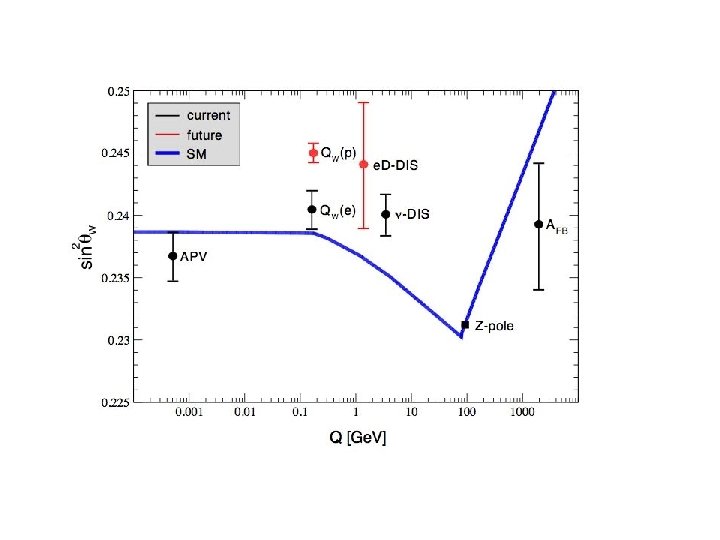
Electroweak Quantum corrections (mt and MH) All coupling constants are functions of a scale (by the way, definition of the mass is also scale dependent). Therefore, different definitions of the sin 2 q. W, which are equivalent in the Born (tree) approximation, depend on the renormalization prescription. There a number of popular schemes leading to values which differ by small factors depending on mt and MH. dependence? What about Appelquist--Carazzone decoupling theorem? T. Appelquist & J. Carazzone, Phys. Rev. D 11 (1975) 2856

In QED and QCD the vacuum polarization contribution of a heavy fermion pair is suppressed by inverse powers of the fermion mass. At low energies, the information on the heavy fermions is then lost. This ‘decoupling’ of the heavy fields happens in theories with only vector couplings and an exact gauge symmetry, where the effects generated by the heavy particles can always be reabsorbed into a redefinition of the low-energy parameters. The SM involves, however, a broken chiral gauge symmetry. Therefore, the electroweak quantum corrections offer the possibility to be sensitive to heavy particles, which cannot be kinematically accessed, through their virtual loop effect. The vacuum polarization contributions induced by a heavy top generate corrections to the W± and Z propagators, which increase quadratically with the top mass [M. Veltman, Nucl. Phys. B 123 (1977) 89]. Therefore, a heavy top does not decouple. For instance, with mt = 171 Ge. V, the leading quadratic correction to amounts to a sizeable 3% effect. The quadratic mass contribution originates in the strong breaking of weak isospin generated by the top and bottom quark masses, i. e. , the effect is actually proportional to. Owing to an accidental SO(3)C symmetry of the scalar sector (the so-called custodial symmetry), the virtual production of Higgs particles does not generate any quadratic dependence on the Higgs mass at one loop [again M. Veltman]. The dependence on MH is only logarithmic. The numerical size of the corresponding correction to varies from a 0. 1% to a 1% effect for MH in the range from 100 to 1000 Ge. V.

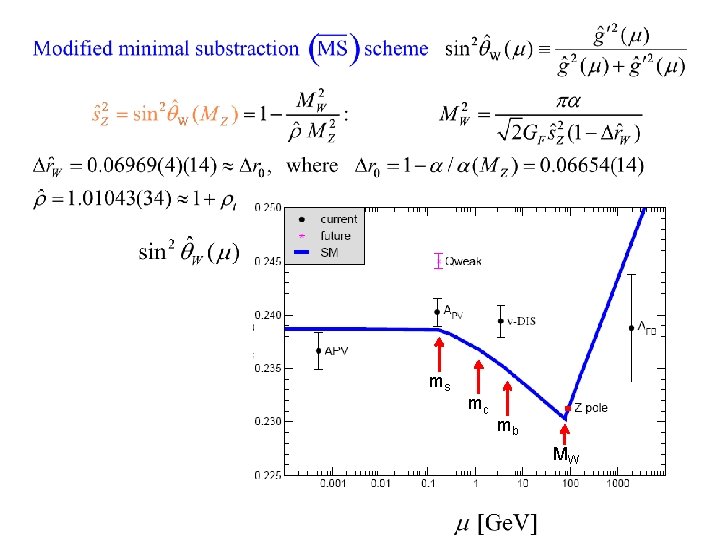
ms mc mb MW

Atomic parity violation (APV) At tree level, r = k = 1, l = 0. For atomic parity violation and the SLAC polarized electron experiment,

For heavy atoms one determines the “weak charge” The parity-nonconserving measurements (PNC) are interpreted in terms of the weak nuclear charge QW, which quantifies the strength of the electroweak coupling between atomic electrons and quarks in the nucleus. The relation between QW and the PNC amplitude, EPNC, can be represented as EPNC = k QW, where k is an atomic-structure factor. Apparently, the interpretation requires atomicstructure calculations of k with an accuracy that matches the experimental uncertainty in EPNC. So far the most accurate measurement has been carried out in 133 Cs. The theoretical uncertainties for the other atoms, thallium, lead and bismuth are larger than 3%.

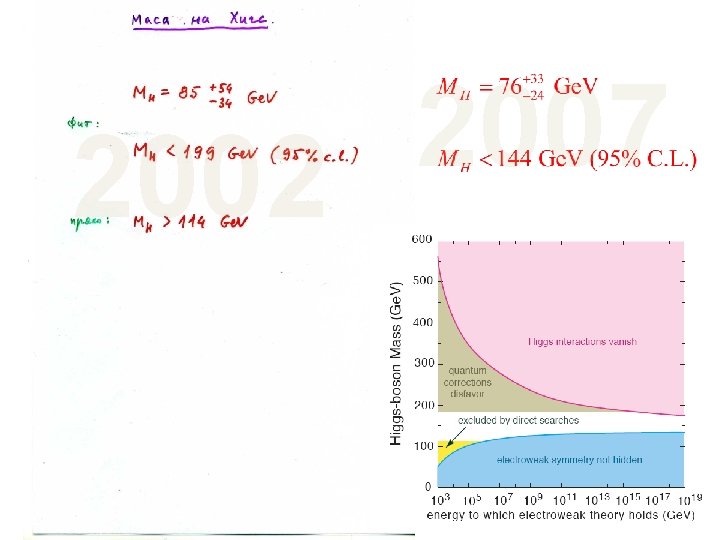
2002

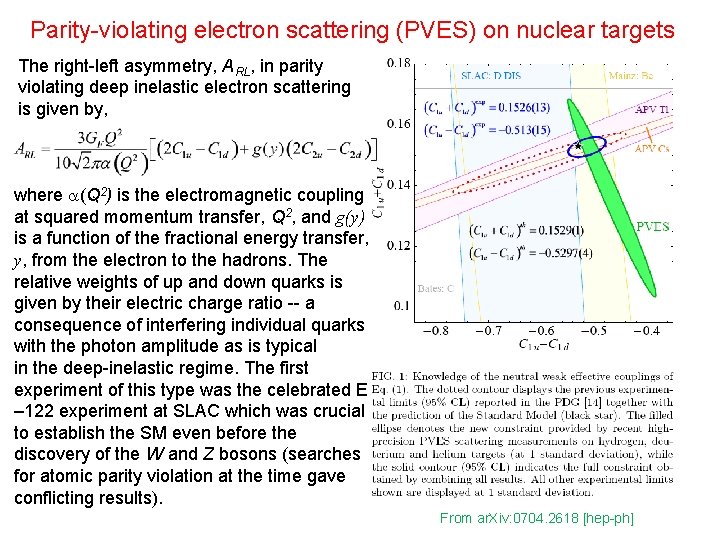
Parity-violating electron scattering (PVES) on nuclear targets The right-left asymmetry, ARL, in parity violating deep inelastic electron scattering is given by, where a(Q 2) is the electromagnetic coupling at squared momentum transfer, Q 2, and g(y) is a function of the fractional energy transfer, y, from the electron to the hadrons. The relative weights of up and down quarks is given by their electric charge ratio -- a consequence of interfering individual quarks with the photon amplitude as is typical in the deep-inelastic regime. The first experiment of this type was the celebrated E – 122 experiment at SLAC which was crucial to establish the SM even before the discovery of the W and Z bosons (searches for atomic parity violation at the time gave conflicting results). From ar. Xiv: 0704. 2618 [hep-ph]

Polarized Møller (electron-electron) Scattering An experiment free of QCD issues has been completed recently by the E– 158 Collaboration. They obtained the first measurement of the parity violating Møller asymmetry, The resulting Qe. W = − 0. 0403± 0. 0053, is in reasonable agreement with the SM prediction. Q-weak A very similar experiment, in fact using the same kind of target (hydrogen), will measure the analogous weak charge of the proton, Qp. W = 2 C 1 u +C 1 d at average Q 2= 0. 03 Ge. V 2. With an expected polarization of 85± 1% the Q-weak Collaboration anticipates to measure the parity violating asymmetry,

Nu. Te. V Nu. Tev Collaboration, Phys. Rev. Lett. 88 (2002) 091802 3 s S. Davidson et al. , JHEP 02 (2002) 037

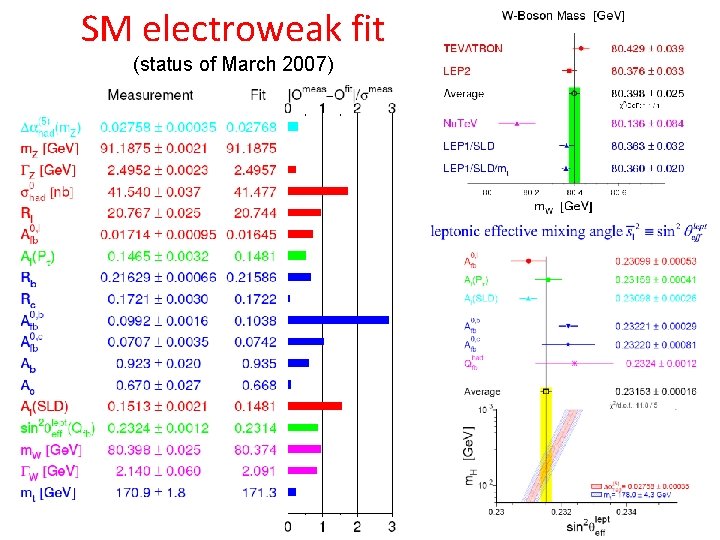
SM electroweak fit (status of March 2007)

2002

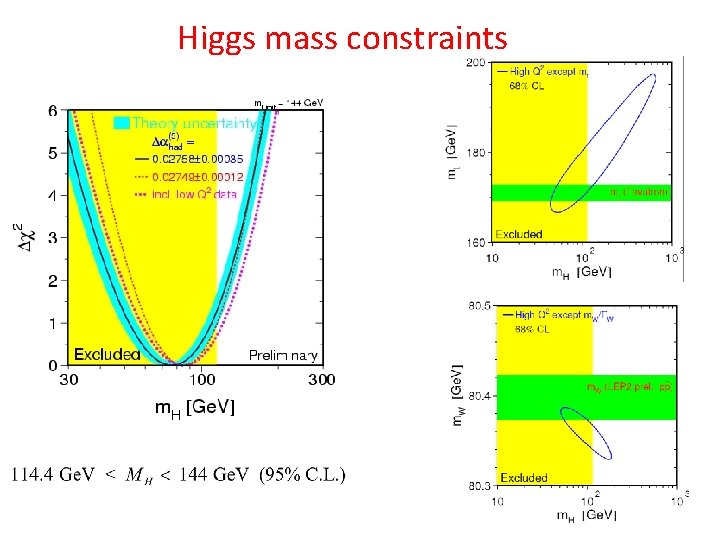
Higgs mass constraints

2007 2002