Particle Physics 5 th Handout Electroweak Theory 1

Particle Physics 5 th Handout Electroweak Theory 1. Divergences: cancellation requires introduce W, introduce Z, introduce Higgs 2. Gauge theories: gauge symmetries bosons, introduction of W+Z; Problems with massive W+Zs the Higgs. http: //ppewww. ph. gla. ac. uk/~parkes/teaching/PP/PP. html Chris Parkes

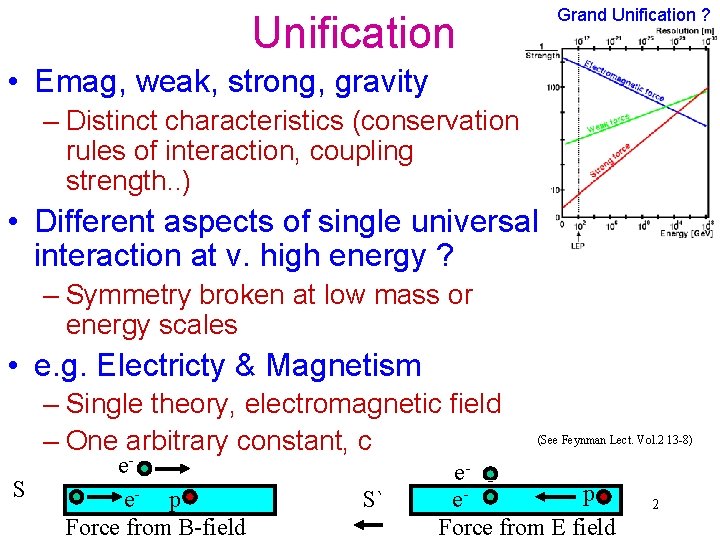
Grand Unification ? Unification • Emag, weak, strong, gravity – Distinct characteristics (conservation rules of interaction, coupling strength. . ) • Different aspects of single universal interaction at v. high energy ? – Symmetry broken at low mass or energy scales • e. g. Electricty & Magnetism – Single theory, electromagnetic field – One arbitrary constant, c S ee- p Force from B-field S` (See Feynman Lect. Vol. 2 13 -8) ep e. Force from E field 2

Electroweak • Electromagnetic and Weak – Different aspects of single electroweak interaction – Same coupling e – Low energy broken symmetry – Massless , massive W+, W-, Z

Divergences See Perkins, Intro to HEP, 3 rd edition chapter 9 • Predicted amplitudes for physical processes finite at all energies, orders of coupling constants – QED arbitrary parameters h, e, m(electron) • Fermi Weak Theory – point-like contact interaction • Elastic Scattering process – Scattered intensity cannot exceed incident intensity – Unitarity limit • Cross-section exceeds wave theory limit – xsec grows as s, – i. e. at some point more particles out than you put in ! 4

Divergences – Add W • Introduce W boson – Propagator – ‘spread’ interaction over finite range W Propagator term • For q 2 large, tends to WCoupling strength, propagator • Cancels s dependence – i. e. well behaved at high energy • BUT diverergences appear in other processes • Need to systematically cancel them 5

Divergences – Add Z • Diagrams contribute to amplitude • Total xsec well behaved • Divergences with QED diagrams as well as W – Adding Neutral currents solves divergences 6

Divergence in Electroweak 1) Electroweak - Cancel all divergences – well behaved theory – Photon and weak couplings related – unification – Same intrinsic coupling strength (numerical factors neglected) 2) Works exactly if electron mass=0 – For finite electron mass need to add Higgs boson also

Unification Conditions (g. Z depends on particles at vertex, discuss form later) Predicts mass MW At low energy W interaction strength given by GF Fermi constant 8

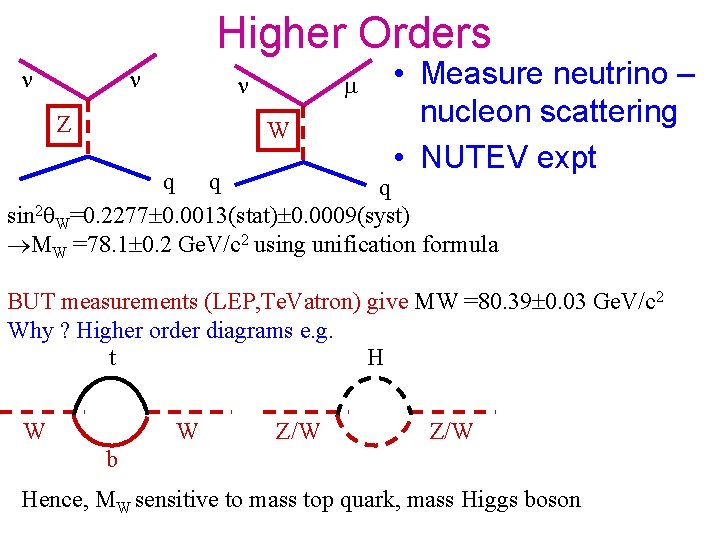
Higher Orders Z W • Measure neutrino – nucleon scattering • NUTEV expt q q q sin 2θW=0. 2277 0. 0013(stat) 0. 0009(syst) MW =78. 1 0. 2 Ge. V/c 2 using unification formula BUT measurements (LEP, Te. Vatron) give MW =80. 39 0. 03 Ge. V/c 2 Why ? Higher order diagrams e. g. H t W W Z/W b Hence, MW sensitive to mass top quark, mass Higgs boson

• In Q. M. connection between Global transformations and conserved quantities, e. g. 1. 2. 3. Translational Invariance Linear momentum conservation Rotational Invariance Angular momentum conservation Translations in time Energy conservation Noether’s theorem – Symmetries (invariances) naturally lead to conserved quantities Emmy Noether Gauge Transformations Schrodinger or Dirac eqn of form: So, ψ’ still satisfies eqn of motion no change in 10 Physics invariant under Global transformation of this form (known as U(1))

Local Gauge Transform - QED • Now consider local transformation Phase θ different at every point is space-time • Ψ’ no longer a solution of eqn of motion for free particle • Add Electromagnetism – – Can now be made invariant ! i. e. invariance under U(1) local transformation electromagnetic field • (Conserved quantity is electric charge) • Interpretation: 1. Change of phase change in E, p • Exactly compensated by changes in emag. Field 2. Emag field carries changes away • Virtual photons • so, photon massless 3. To cancel over all space-time range must be 11

Local Gauge Transform - QCD • This time use colour state of quark • 3 component vector Λ in r, g, b, space • Symmetry group is SU(3) • λ are matrices which transform the colour state – 8 basis states • i. e. SU(3) gauge symmetry 8 massless, coloured gluons 12

Weak Interactions • So QED local gauge QCD • What about weak ? • Need nature of particle also to change • Transform • Symmetry group SU(2) – Λ is a 2 component vector – Τ are the matrix states 13

Weak Transform Generators of SU(2) T are Pauli matrices: 3 basis states W+, W-, W 0 Arrange particles in pairs in generations: Left-handed doublet Right-handed singlet Weak force acts on LH Caveat: RH neutrinos? Weak Isospin space – up and down components e. g. 14

Electroweak Transform • Combined Electroweak – Symmetry SU(2)x. U(1) – Triplet (W , W 0) and singlet (B 0) of massless ( range) fields – Predicts W+, W-, neutral currents, photon – Explains Fermi theory, cancels divergences • Two problems remain: 1. W 0 same form and strength as W • But not true experimentally And g. Z depends on particles at vertex 2. W+, W-, W 0 all predicted massless • But heavy, W ~ 80 Ge. V/c 2 , Z ~91 Ge. V/c 2 15

Problem 1: neutral bosons 0 0 0 • Clearly , Z related to W , B but how ? • Mixtures • W - weak force – couples left-handed particle states discussed earlier • Z – mixture weak & electromagnetic – Emag part couples to electric charge of particle • Same for LH, RH parts – Weak part couples to weak isospin • i. e. only to RH part of particle – e. g. ν – only weak component of coupling e- - weak part & emag part for charge 1 u - weak part & emag part for charge 2/3 Mixtures give rise to unification condition relate , W, Z couplings 16 and explain g. Z variation with particle type

Problem 2: Masses for W & Z • Gauge invariance leads to zero masses – Need to cancel at infinite range – QED – massless – QCD – massless g • BUT not for (Electro)Weak • Overcome by introducing Higgs Field Mechanism to: • give particles masses • make theory gauge invariant Higgs boson is the quanta of the Higgs field. Only particle in SM not discovered

Higgs Mechanism http: //hepwww. ph. qmw. ac. uk/epp/higgs. html • Cocktail party – People at party ! – Higgs field is NOT empty • An ex-PM arrives – People cluster around her – She acquires mass from the Higgs field • Rumour passes through room – Cluster of people – Excitation of Higgs field – Higgs boson

Higgs Field • Introduce doublet of scalar fields • Vacuum state – Not zero • Emag bowl shaped – Vacuum field 0 • Higgs field, “Mexican Hat”-like – Vacuum expectation value of field, v • Ground state is degenerate – Spontaneous symmetry breaking Redefine all fields wrt physical vacuum Potential Energy not symmetric about this point Symmetry between W and B fields is broken 19

Higgs Mechanism Predictions • 1) W and Z acquire masses – Masses from interaction of gauge fields with non-zero vac. expectation value, v, of Higgs Field • 2) Neutral spin-zero Higgs bosons H – Quanta of Higgs field from gauge invariance • 3) Particle masses – Particles travel through Higgs field and acquire masses – Fermions/bosons also interact with Higgs boson H f – Coupling proportional to particle mass f 20 Standard Model does not predict Higgs mass, W/Z mass, fermion masses

Electroweak Summary • Electroweak theory provides well-behaved theory without divergences • Gauge invariance leads to introduction of weak force • Higgs Mechanism leads to particle masses • Tests of Theory: – Find Neutral Currents – Discover W, Z bosons – Measure W, Z couplings and masses – Find Higgs Boson ?