Particle Motion Refresher on translational kinematics and kinetics

Particle Motion Refresher on translational kinematics and kinetics. Linear momentum, Newton’s laws, coordinate frames. Examples from aircraft performance, orbital mechanics, and launch vehicle trajectories.

Newton’s Second Law ~f = m~a • Applicable to mass particles with constant mass and zero volume – extensible to rigid bodies • Not as simple as it looks – Determination of the force usually requires free -body diagram – can be extremely complicated – Determination of the acceleration sometimes involves complicated kinematics – Acceleration is second derivative of position vector with respect to time

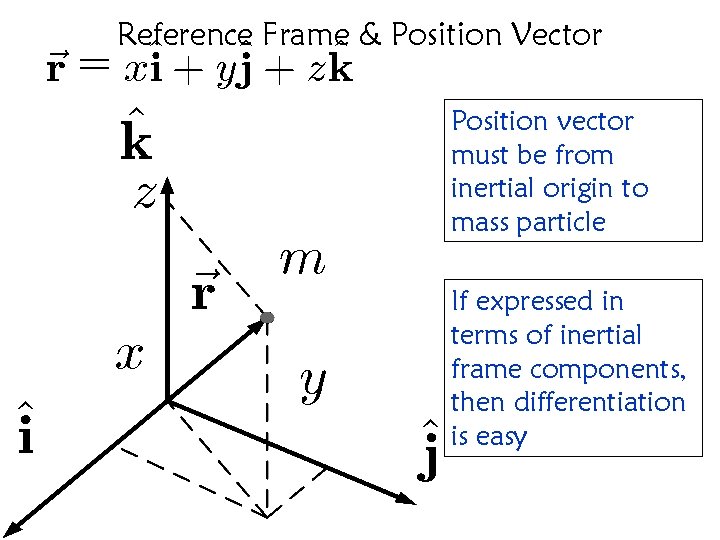
Reference Frame & Position Vector ^ ~r = x^i + y^j + z k Position vector must be from inertial origin to mass particle ^ k z ~r x ^i m y ^j If expressed in terms of inertial frame components, then differentiation is easy

Inertial Origin • An inertial origin is a point that is not accelerating with respect to any other inertial origin – Alternatively, an inertial origin is a point for which Newton’s laws are applicable – There is no known inertial origin, but for most problems an origin can be found that is “inertial enough” – For some problems, an Earth-fixed reference point is sufficient, whereas for others, the rotation of the Earth must be considered

Inertial Reference Frame • An inertial reference frame is a set of three unit vectors that are mutually perpendicular, with their origins at a single inertial origin, and whose directions remain fixed with respect to inertial space – Alternatively, an inertial reference frame is a frame for which Newton’s laws are applicable – Usually the d&c analyst must determine the simplest frame that is “inertial enough” – What about these vehicles? • Paper airplane, Cessna 152, B 2, container ship, Space Shuttle, Apollo 11, Cassini, Rama

Reference Frames • A reference frame is a set of three mutually perpendicular (orthogonal) unit vectors • Typical notations include • Typical reference frames of interest for vehicles include – – – ECI (Earth-centered inertial) Perifocal (Earth-centered, orbit-based inertial) ECEF (Earth-centered, Earth-fixed, rotating) Orbital (Earth-centered, orbit-based, rotating) Wind (vehicle-centered, rotating) Body (vehicle-fixed, rotating)

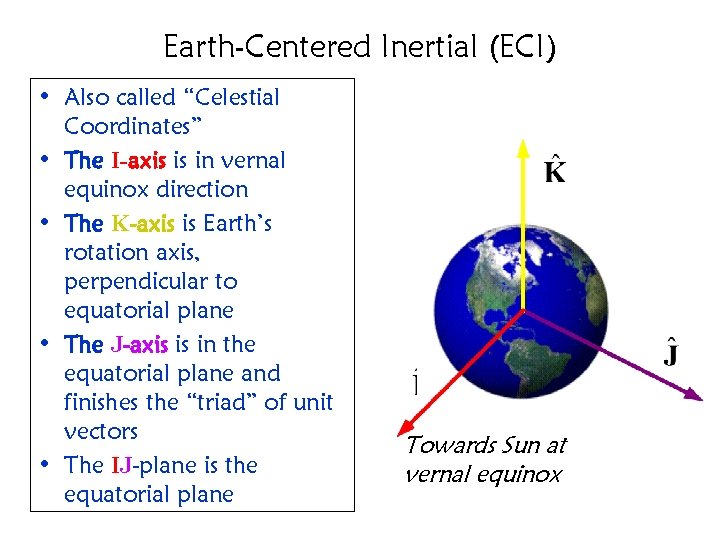
Earth-Centered Inertial (ECI) • Also called “Celestial Coordinates” • The I-axis is in vernal equinox direction • The K-axis is Earth’s rotation axis, perpendicular to equatorial plane • The J-axis is in the equatorial plane and finishes the “triad” of unit vectors • The IJ-plane is the equatorial plane Towards Sun at vernal equinox

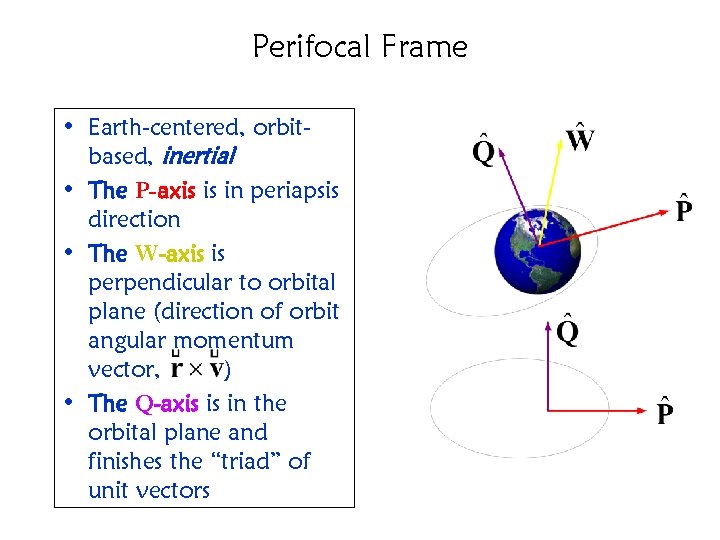
Perifocal Frame • Earth-centered, orbitbased, inertial • The P-axis is in periapsis direction • The W-axis is perpendicular to orbital plane (direction of orbit angular momentum vector, ) • The Q-axis is in the orbital plane and finishes the “triad” of unit vectors

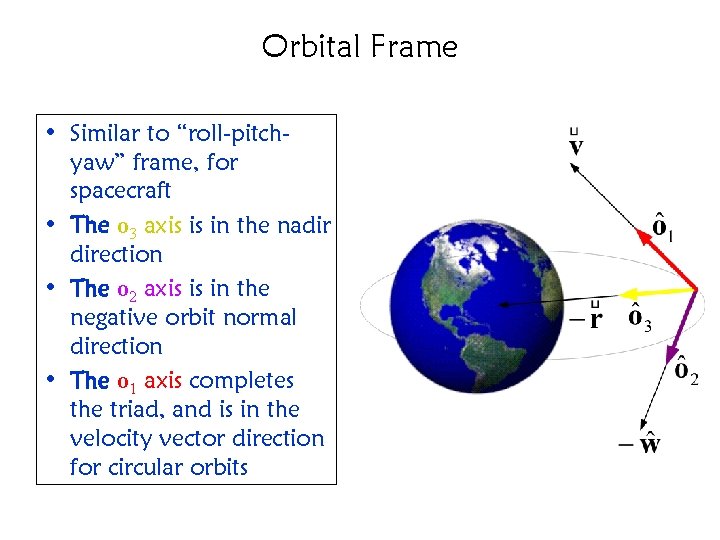
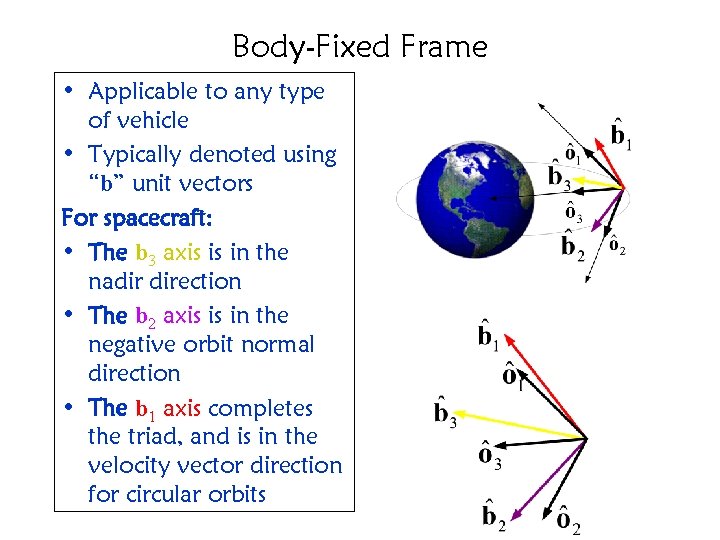
Orbital Frame • Similar to “roll-pitchyaw” frame, for spacecraft • The o 3 axis is in the nadir direction • The o 2 axis is in the negative orbit normal direction • The o 1 axis completes the triad, and is in the velocity vector direction for circular orbits

Body-Fixed Frame • Applicable to any type of vehicle • Typically denoted using “b” unit vectors For spacecraft: • The b 3 axis is in the nadir direction • The b 2 axis is in the negative orbit normal direction • The b 1 axis completes the triad, and is in the velocity vector direction for circular orbits

Vector, Frame, and Matrix Notation n. Symbolo ~v ^i ; ^i 1 n F 2 o 3 i ^i vi vb Rbi µ ~ ! ~ bi ! ! bi b ! bi a Meaning vector, an abstract mathematical object and length n with direction o the three unit base vectors of a reference frame the reference frame with base vectors ^i 1 ; ^i 2 ; ^i 3 a column matrix whose 3 elements are the unit vectors of a column matrix whose 3 elements are the components F of the vector ~v expressed in i a column matrix whose 3 elements are the components F of the vector ~v expressed in b F F rotation matrix that transforms vectors from i to b a column matrix whose 3 elements are the Euler angles µ 1 , µ 2 , µ 3 an angular velocity Fvector F angular velocity of Fb with respect to Fi expressed in Fb angular velocity of b with respect to i expressed in a F i

Position, Velocity and Acceleration Vectors ^ ~r = x^i + y^j + z k d ^ ~v = ~r_ = x_^i + y_^j + z_ k dt ^ ~a = ~v_ = x Ä^i + yÄ^j + zÄk ^ k z ~r x ^i m y ^j Derivatives are simple because unit vectors are constant, in direction and magnitude

Application of ~f = m~a ³ the components ´ of the force vector Need to know ~f ^ = f ^i + f ^j + f k x y z ^i + yÄ^j + zÄk ^ = m x Ä ) fx fy fz = mÄ x = mÄ y = mÄ z Three second-order ordinary differential equations. Linearity and coupling depend on nature of forces.

Simple Feedback Control Forces ¡ ¡ Suppose=the forces take the following form fx fy = fz = x x _ k k ¡ px ¡ dx k k y y _ ¡ py ¡ dy kpz z kdz z_ Here the “k” terms are feedback gains, whose values are selected kp by the d&c analyst. The k terms are proportional to the position errors, and d the terms are proportional to the velocity errors, or to the derivatives of the position errors, hence the controller is a “PD” controller

Equations of Motion with PD Control ) First, define some new variables, termed the states x_ 1 = x 4 x 1 = x x 2 = y x_ 2 = x 5 x 3 = z x_ 3 = x 6 ¡ ¡ 1 = x 4 x_ ( kpx x 1 kdx x 4 ) x_ 4 = fx =m = m x 5 = y_ ¡ 1 ¡ ( kpy x 2 kdy x 5 ) x_ 5 = fy =m = x#6 = z_ m ¡ ¡ 1 2 = f =m = ( kpz x 3 kdz x 6 ) _ x 6 6 z R x m x_ = f (x) x is the state vector x_ = f (x; x 0 ; k)

Linear System of Equations (PD Control) • Because of the unique form of these equations, they can be written in matrix form – Each “right-hand side” appears as a summation of constants multiplying states, with the states always appearing linearly – Thus, the equations comprise a system of linear, constant-coefficient ordinary differential equations x_ = f (x) = Ax

Linear System (PD) (continued) Simple rearrangement of the equations of motion leads 2 to the block matrix form: 6 6 0 0 0 1 0 0 6 6 0 0 1 0 6 6 0 0 0 1 ¡ 0 x_ = 4 kpx =m ¡ 0 kdx =m ¡ 0 0 kpy =m ¡ 0 kdy =m ¡ 0 · ¸ 0 0 0 kpz =m 0 0 kdz =m = ¡ 0 1 ¡ diag(kp )=m diag(kd )=m x = Ax Because A is constant, the system is easily solved: x(t) = e. At x 0 3 7 7 7 5 x

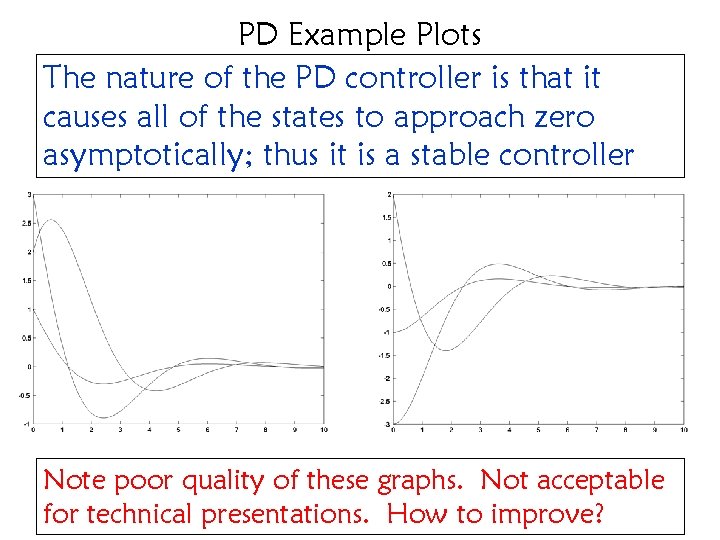
PD Example Plots The nature of the PD controller is that it causes all of the states to approach zero asymptotically; thus it is a stable controller Note poor quality of these graphs. Not acceptable for technical presentations. How to improve?

PD Example Exercise • The lecture notes include the Matlab code for numerical integration of this system of equations – Implement the Matlab code and carry out some simple experimentation with varying gains and initial conditions – Compare the numerically integrated solution to the exact solution on the previous slide • We will return to the closed form solution later in the course

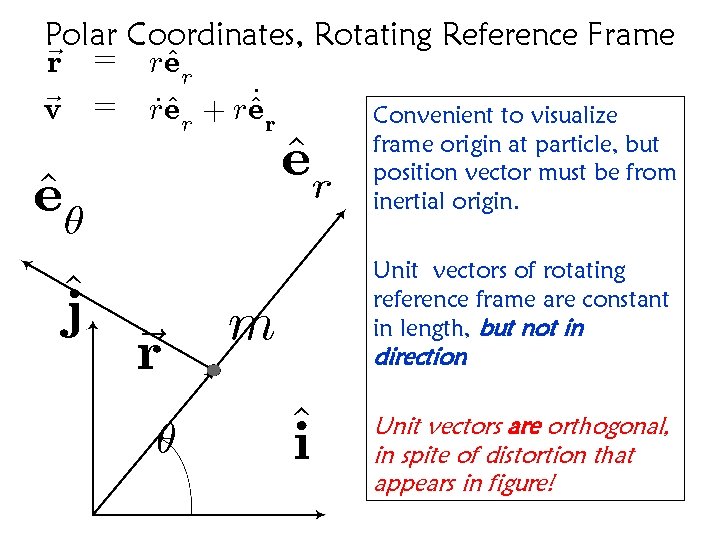
Polar Coordinates, Rotating Reference Frame ~r = r^ er ^_ r ~v = r^ _ er + r e Convenient to visualize ^r e ^µ e ^j ~r µ frame origin at particle, but position vector must be from inertial origin. Unit vectors of rotating reference frame are constant in length, but not in m direction ^i Unit vectors are orthogonal, in spite of distortion that appears in figure!

Rate of Change of the Unit Vectors • The unit vectors change because the angle changes • Denote small change in time t and corresponding change in angle with t and • Consequently, the required derivatives can be written as ¢^ er ¢µ _e _e = lim ^r = lim ^µ = µ^ e ! ! µ ¢t ¢t ¢t 0 ¡ _e ^_ µ = ³ µ^ e ´ ³ ´ r Exercise: convince yourself _e ~v = r^ _ er + rµ^ this limit is correct µ ¡ ^ + rµÄ + 2 r_ µ_ e ^ ~a = rÄ rµ_ 2 e r µ

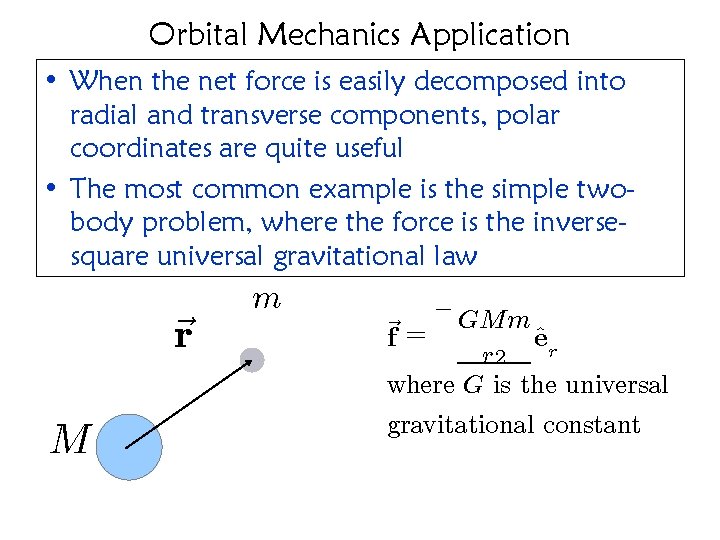
Orbital Mechanics Application • When the net force is easily decomposed into radial and transverse components, polar coordinates are quite useful • The most common example is the simple twobody problem, where the force is the inversesquare universal gravitational law m ~r M ~f = ¡ GMm ^r e r 2 where G is the universal gravitational constant

Simple Orbit Example ¡ mthat GM=1; then the Suppose we select units such ~ ^r e fr = force is r 2 Application of Newton’s 2 nd law leads to the two ¡ ¡ 1 equations: scalar nonlinear ordinary differential rÄ rµ_2 rµÄ + 2 r_ µ_ = r 2 = 0 Why are these equations nonlinear? Exercise: derive these equations

Rewrite as x_ = f (x) ) Define new state variables x_ 1 = x 3 x 1 = r x 2 = µ x_ 2 = x 4 x 3 = r_ x#4 = µ_ x 2 R 4 ¡ 1 x_ 3 = x 1 x 2 4 x 2 ¡ 2 x x 1 3 4 x_ 4 = x 1 x_ = f (x) Note the nonlinearities, as well as the singularity for zero radius

Orbital Mechanics Example (cont) • We can identify a special solution to the equations of motion • Suppose x 1=constant (circular orbit), then x 3=0, so x 4=constant also (constant angular rate) • From the d. e. for x 3 (which must be zero), we can x 3 x 2 = 1 deduce that 1 4 • This result is a form of Kepler’s Third Law, which relates the orbital period to the orbital radius – the “ 1” is a result of our choice of units such that GM=1 Exercise: verify the equivalence between this result and Kepler’s Third Law

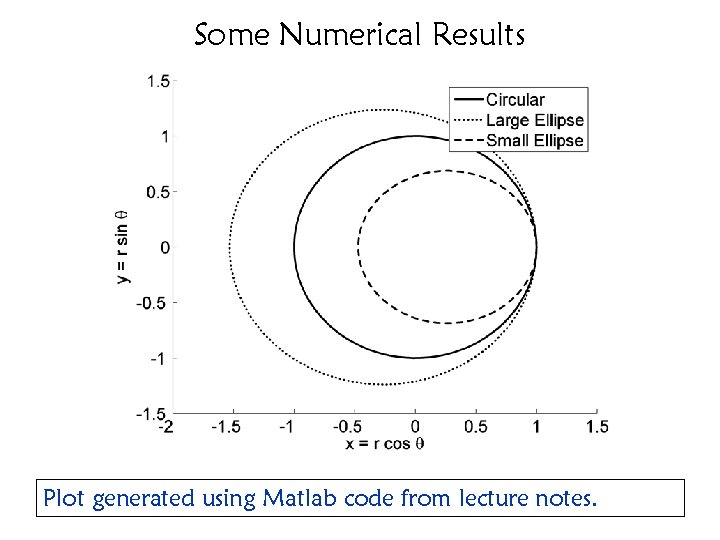
Some Numerical Results Plot generated using Matlab code from lecture notes.

Particle Motion … so far … f=ma Reference frames, inertial origins and frames Position, velocity, acceleration State vector form of EOM “PD” control example Rotating reference frame, polar coordinates Simple orbital motion

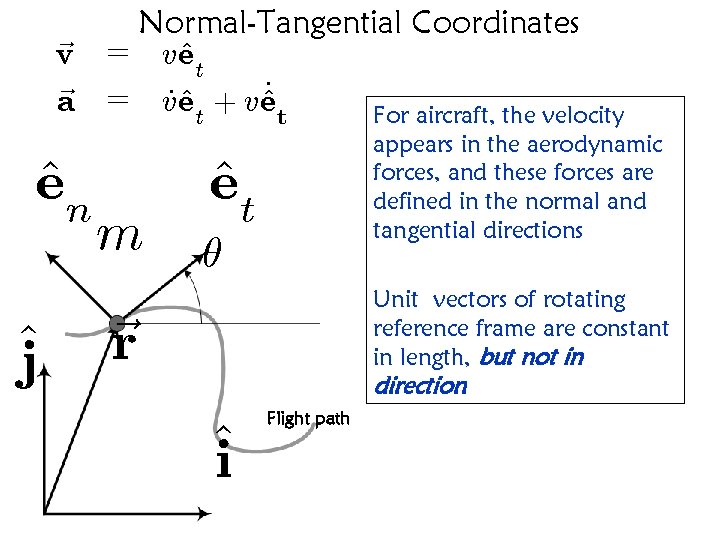
Normal-Tangential Coordinates • For a circular orbit, the radial-transverse frame and coordinates are also normal and tangential to the spacecraft flight path, respectively • We can also define a frame that has these properties for non-circular orbits, but the gravitational force is more complicated in such a frame • This “normal-tangential” frame is well-suited for problems involving aircraft trajectories, since lift and drag are aerodynamic forces defined in the normal and tangential directions, respectively

Normal-Tangential Coordinates ~v = v^ et ~a = v^ ^_ t _ et + v e For aircraft, the velocity ^n e ^j m appears in the aerodynamic forces, and these forces are defined in the normal and tangential directions ^t e µ Unit vectors of rotating reference frame are constant in length, but not in ~r direction ^i Flight path

Rate of Change of the Unit Vectors • The unit vectors change because the angle changes • Denote small change in time t and corresponding change in angle with t and • Consequently, the various derivatives can be written as ^_ t e ^_ n e ~v = = = ~a = _e µ^ ¡n _e µ^ t ^t ve _e _ et + v µ^ v^ n Exercise: convince yourself … Note that if is increasing, then the radius of curvature of the flight ^n path e emanates from the positive direction, whereas if is decreasing, then the radius of curvature emanates ^n e from the negative direction. The normal acceleration (and hence the net normal force) is in the same sense.

Normal-Tangential Coordinates • The speed can generally be written in terms of _ and the radius of curvature as thevangular = r µrate c • Hence the acceleration vector can be written as ^t + ~a = v_ e v 2 e ^n rc • This acceleration vector can be used in a straightforward way in developing the equations of motion for an aircraft modeled as a point mass moving in a vertical plane

Simplest Aircraft Translational Motion The four forces: Lift L, perpendicular to flight path Drag D, parallel to flight path Weight W, toward center of Earth Thrust T, generally inclined wrt flight path ^n e L c T T e n i l d hor D W ^t e

nd Law Application¡of Newton’s 2 ¡ ^t : T cos ®T D W sin µ = mv_ e ¡ v 2 ^n : T sin ®T + L W cos µ = m e rc • The simplest) problem is 1 the case of straight, level, non-accelerating = for T=0 ) rflight, c – Straight µ=0 – Level ¡ – Equations simplify: ^t : T ¡ D e ^n : L W e = 0

Thrust Required for Straight, Level Flight • Solve thrust=drag, lift=weight equations obtain required thrust T =to W=(L=D) R • Obvious conclusion: required thrust is minimized when L/D is maximized • Further analysis requires stating lift and drag in terms of velocity and dynamic pressure q = 1 ½v 2 2 • Dynamic pressure: where is atmospheric density

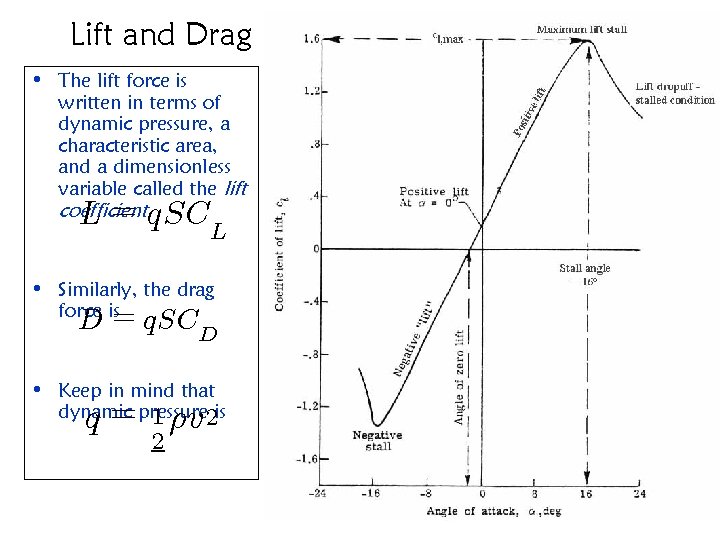
Lift and Drag • The lift force is written in terms of dynamic pressure, a characteristic area, and a dimensionless variable called the lift coefficient L = q. SCL • Similarly, the drag force is= D q. SCD • Keep in mind that dynamic pressure 1 2 is q = ½v 2

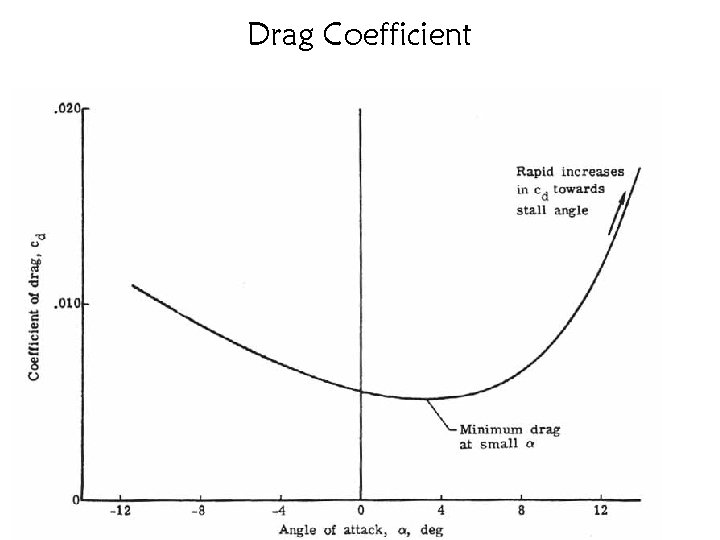
Drag Coefficient

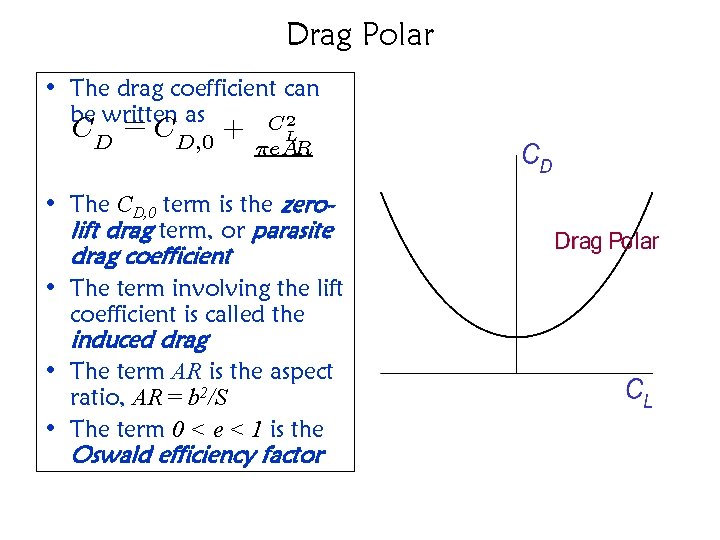
Drag Polar • The drag coefficient can be written C 2 = as CD CD; 0 + L ¼e. AR • The CD, 0 term is the zerolift drag term, or parasite drag coefficient • The term involving the lift coefficient is called the induced drag • The term AR is the aspect ratio, AR = b 2/S • The term 0 < e < 1 is the Oswald efficiency factor

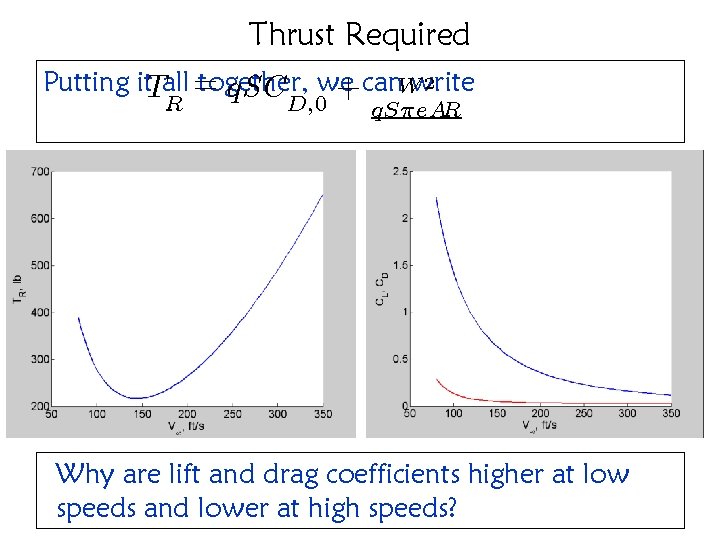
Thrust Required 2 Putting it. Tall = together, q. SC we + can. Wwrite R D; 0 q. S¼e. AR Why are lift and drag coefficients higher at low speeds and lower at high speeds?

Lagrange’s Equations • Brief treatment applicable only to systems of n particles subject only to conservative forces • Basic idea: – Write down the position vectors of the n particles in terms of independent generalized coordinates – Differentiate the position vectors to get velocity vectors in terms of generalized velocities – Write down the kinetic energy, T – Write down the potential energy, V – Form the Lagrangian, L=T-V – Take derivatives of the Lagrangian to get the differential equations of motion

Lagrange’s Equations (2) • The position vectors must be written in terms of independent generalized coordinates, denoted qk, k=1, …, N – For example, for a particle with unconstrained motion in three dimensions, one might use q 1=x, q 2=y, q 3=z – For a particle constrained to move on a circle in a plane (e. g. , a pendulum), there is only one degree of freedom, so one might use q 1=q – In general, the position vectors are written as ~ri = ~ri (q) _ ~vi = ~r_ i (q; q) – Consequently, the velocity vectors are

Lagrange’s Equations (3) • The potential energy depends only on the positions ) =particle V = Vof(~rthe V (q) i ¢ • The. T kinetic velocities = 1 §energy n m ~ ~v =on _ vdepends q) T (q; 2 i=1 i i i • Thus the Lagrangian depends on ¡ generalized _ velocities q) L = T coordinates V = L(q; and

Lagrange’s Equations (4) ¡ ¢¢¢ • Take the derivatives of the Lagrangian: d @L @L = 0; k = 1; dt @q_k @qk ; N • This step gives N second-order ordinary differential equations describing the motion of the n particles • If there were non-conservative forces acting on the system of particles, then the right-hand sides of these equations would have non-zero terms, called generalized forces.

Lagrange’s Equations Example Consider a single particle of mass m connected to a linear spring with spring constant k, suspended in a constant gravitational field with acceleration g, and constrained to move in a vertical plane, i. e. , an elastic planar pendulum. Assume, for simplicity, that the unstretched length of the spring is zero. Use polar coordinates, measured from the fixed end of the spring. The = r^ position of the ~rparticle ewith respect to this inertial origin is r The potential energy = associated with the spring is Vs kr 2 =2 ¡ The potential energy = associated with gravity is Vg where µ mgr cos µ is the angle between ^r e and the downward direction

Lagrange’s Equations Example (2) ³ ´ _ _ ~v = ~r = r^ eµ _ er + rµ^ 1 ³¢ 1 ´ = = T m~v ~v m r_ 2 + r 2 µ_2 2 2 ¡ ¡ 1 1 L = T V = m r_ 2 + r 2 µ_ 2 kr 2 + mgr cos µ 2 2 All that remains is to take the required derivatives of this scalar function with respect to the generalized coordinates and velocities, obtaining the two secondorder di®erential equations of motion: ¡ ¡ mÄ r mrµ_ 2 + kr mg cos µ = 0 mr 2 µÄ + 2 mrr_ µ_ + mgr sin µ = 0 An interesting exercise is to re-derive these equations by direct application of Newton's Second Law.