Particle Identification Cherenkov Radiation Transition Radiation TimeofFlight 2











- Slides: 40


Particle Identification Cherenkov Radiation Transition Radiation Time-of-Flight 2

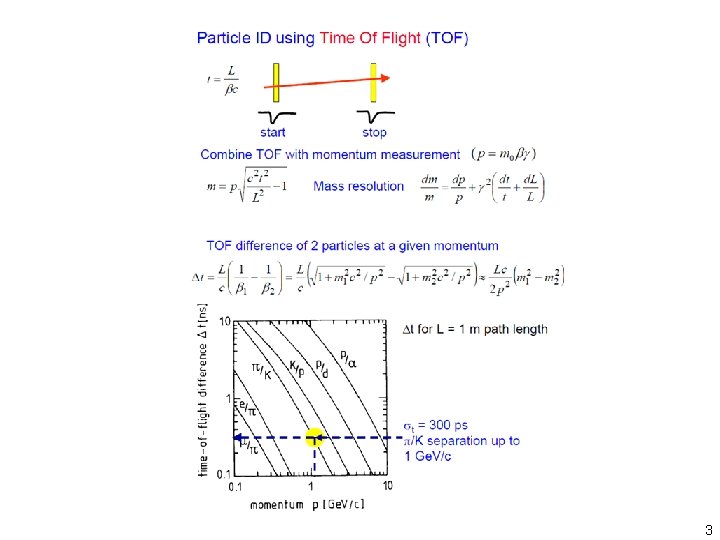
3

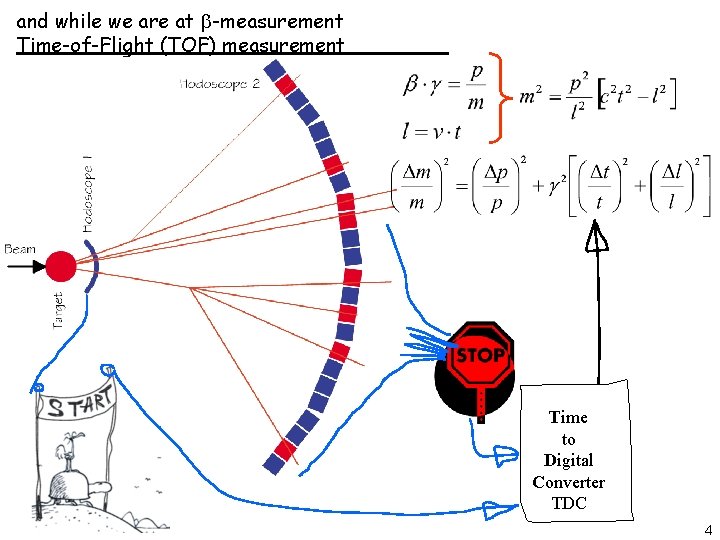
and while we are at b-measurement Time-of-Flight (TOF) measurement Time to Digital Converter TDC 4

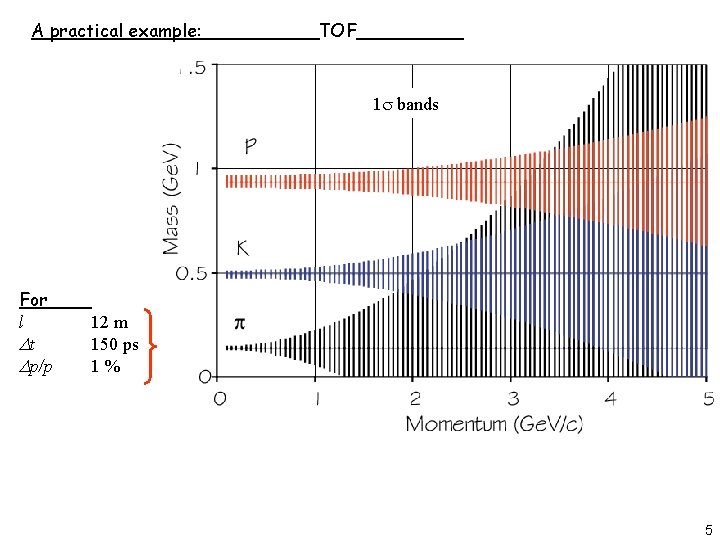
A practical example: TOF 1 s bands For l Dt Dp/p 12 m 150 ps 1% 5

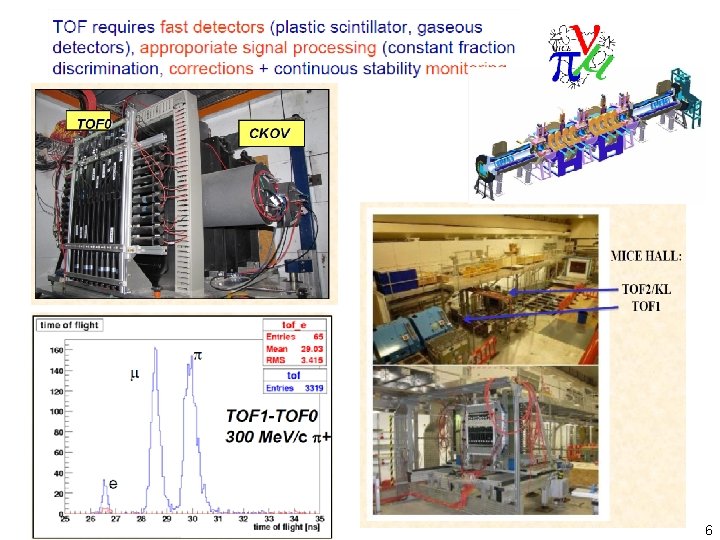
6

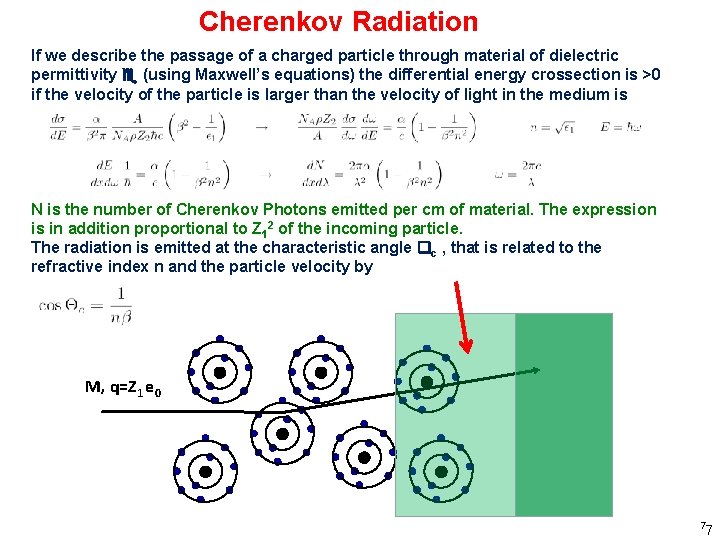
Cherenkov Radiation If we describe the passage of a charged particle through material of dielectric permittivity (using Maxwell’s equations) the differential energy crossection is >0 if the velocity of the particle is larger than the velocity of light in the medium is N is the number of Cherenkov Photons emitted per cm of material. The expression is in addition proportional to Z 12 of the incoming particle. The radiation is emitted at the characteristic angle c , that is related to the refractive index n and the particle velocity by M, q=Z 1 e 0 7 7

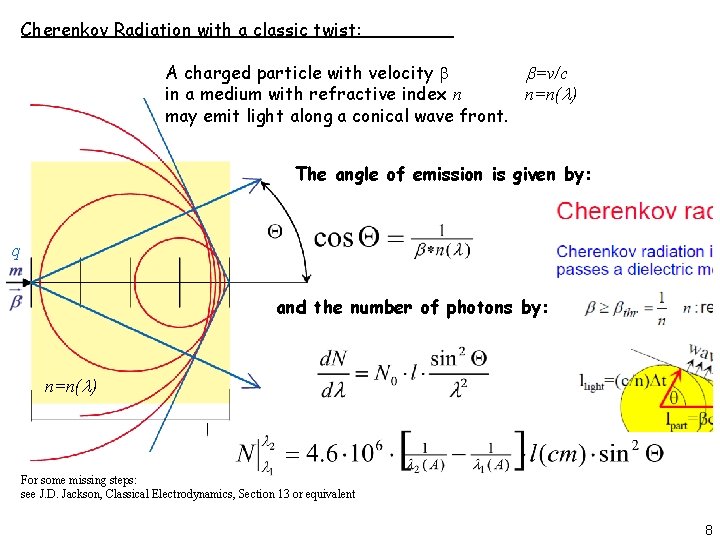
Cherenkov Radiation with a classic twist: A charged particle with velocity b b=v/c in a medium with refractive index n n=n(l) may emit light along a conical wave front. The angle of emission is given by: q and the number of photons by: n=n(l) For some missing steps: see J. D. Jackson, Classical Electrodynamics, Section 13 or equivalent 8

12

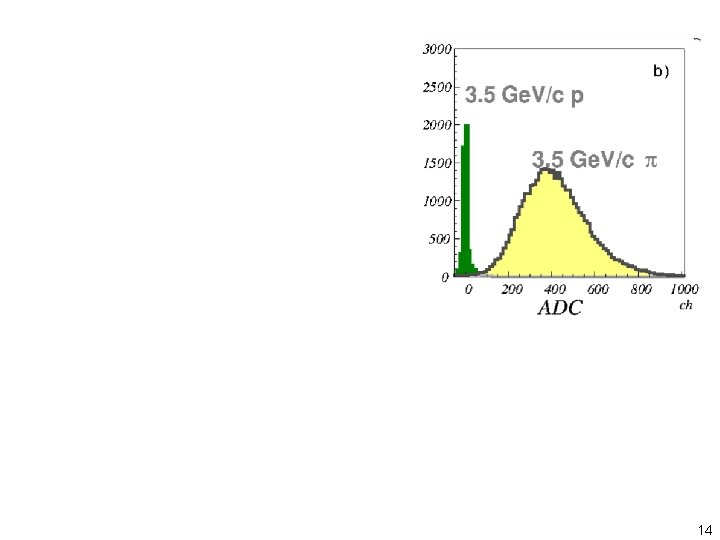
14

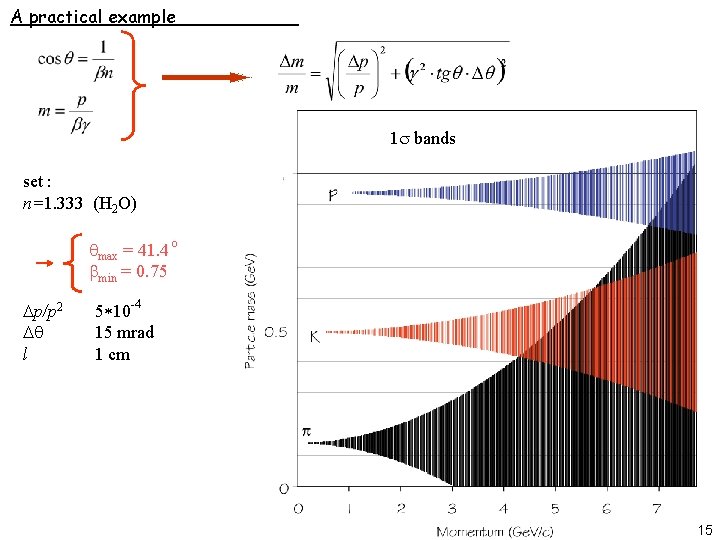
A practical example 1 s bands set : n=1. 333 (H 2 O) qmax = 41. 4 o bmin = 0. 75 p/p 2 q l 5*10 -4 15 mrad 1 cm 15

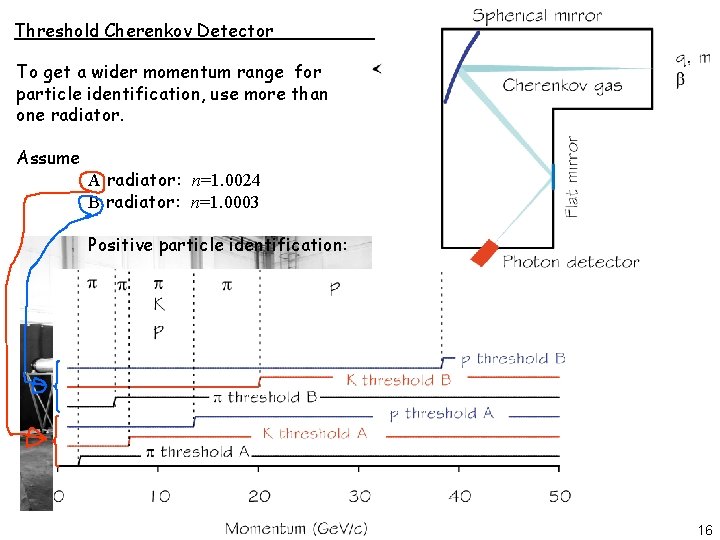
Threshold Cherenkov Detector To get a wider momentum range for particle identification, use more than one radiator. Assume A radiator: n=1. 0024 B radiator: n=1. 0003 Positive particle identification: A gas Cherenkov counter as used to tag particles in the secondary beams Apr 1963 Photo number: CERN-IT-6304088 16

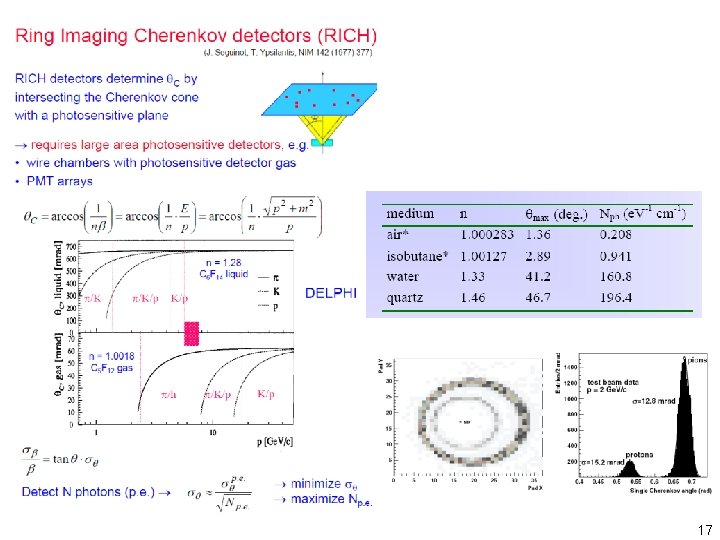
17

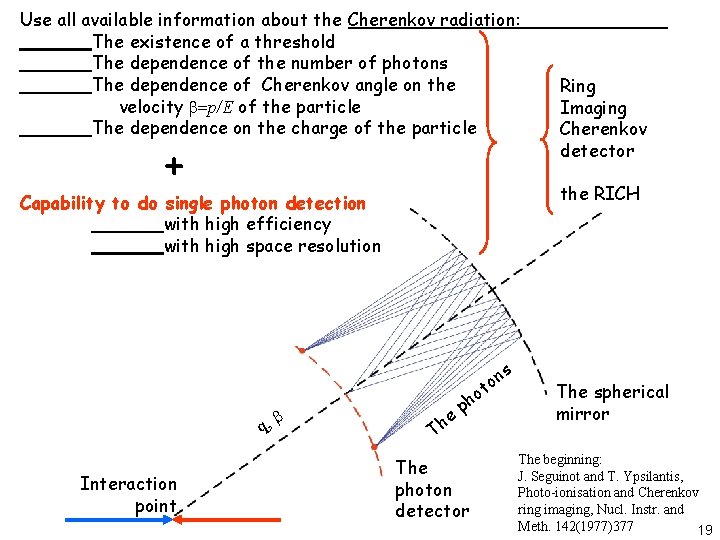
Use all available information about the Cherenkov radiation: The existence of a threshold The dependence of the number of photons The dependence of Cherenkov angle on the velocity b=p/E of the particle The dependence on the charge of the particle + the RICH Capability to do single photon detection with high efficiency with high space resolution s n to q, b Interaction point Ring Imaging Cherenkov detector e h T o ph The photon detector The spherical mirror The beginning: J. Seguinot and T. Ypsilantis, Photo-ionisation and Cherenkov ring imaging, Nucl. Instr. and Meth. 142(1977)377 19

20

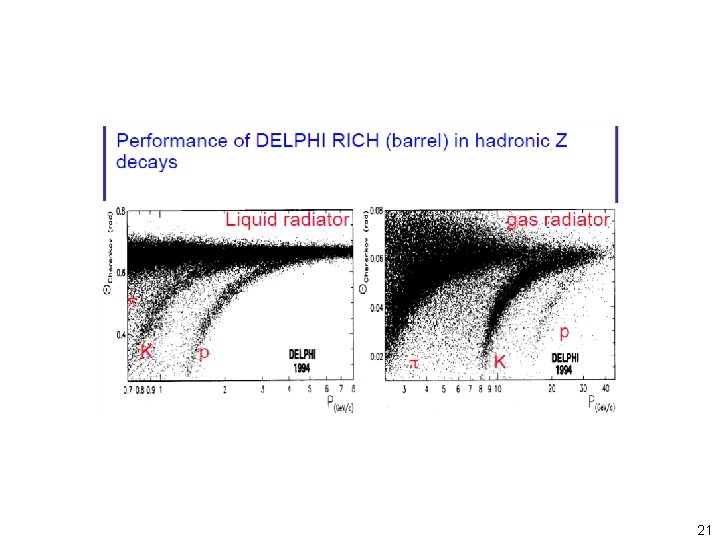
21

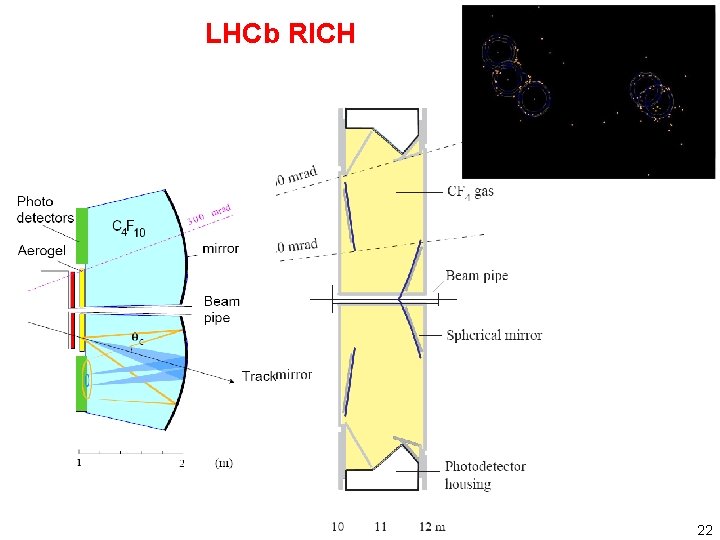
LHCb RICH 22

LHCb RICH 2 23

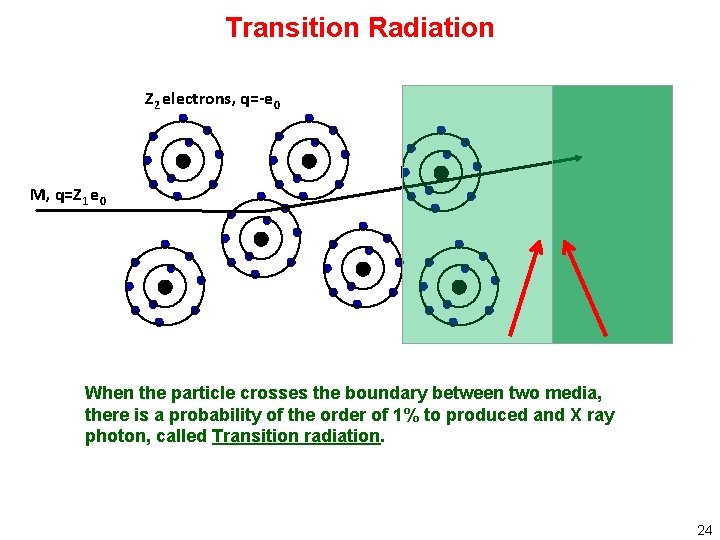
Transition Radiation Z 2 electrons, q=-e 0 M, q=Z 1 e 0 When the particle crosses the boundary between two media, there is a probability of the order of 1% to produced and X ray photon, called Transition radiation. 24

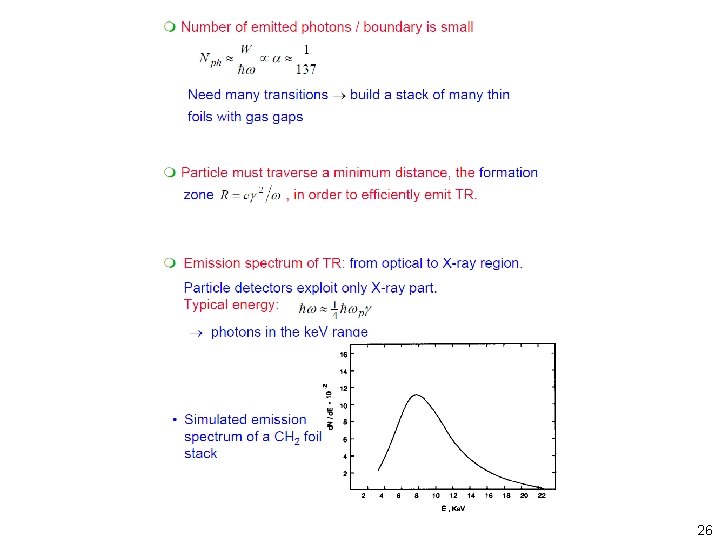
25

26

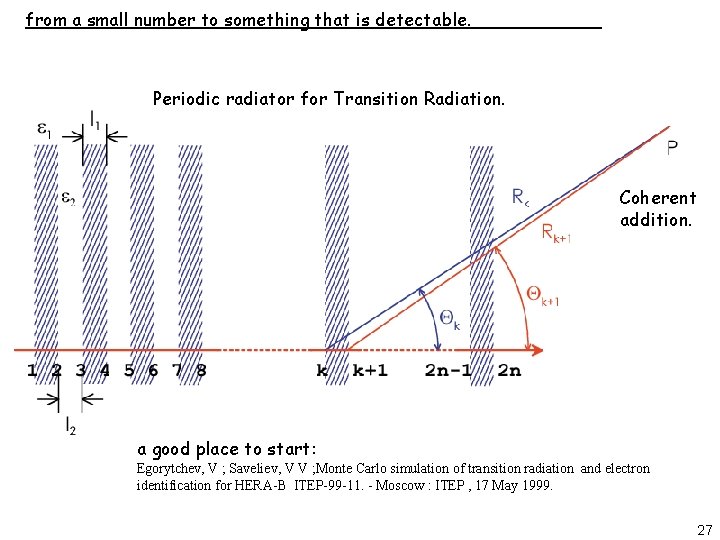
from a small number to something that is detectable. Periodic radiator for Transition Radiation. Coherent addition. a good place to start: Egorytchev, V ; Saveliev, V V ; Monte Carlo simulation of transition radiation and electron identification for HERA-B ITEP-99 -11. - Moscow : ITEP , 17 May 1999. 27

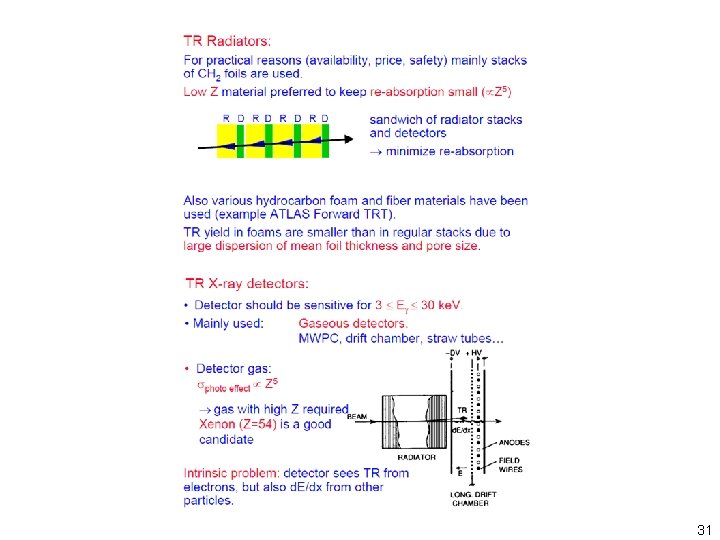
31

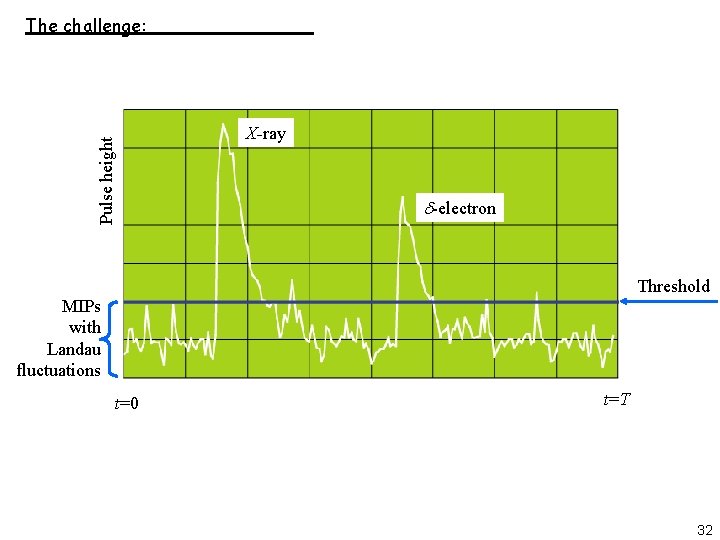
Pulse height The challenge: X-ray d-electron Threshold MIPs with Landau fluctuations t=0 t=T 32

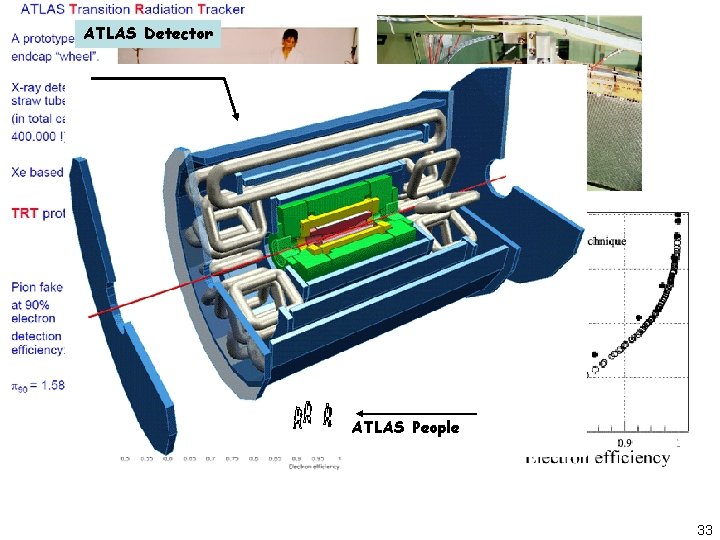
ATLAS Detector test-beam data ATLAS People 33

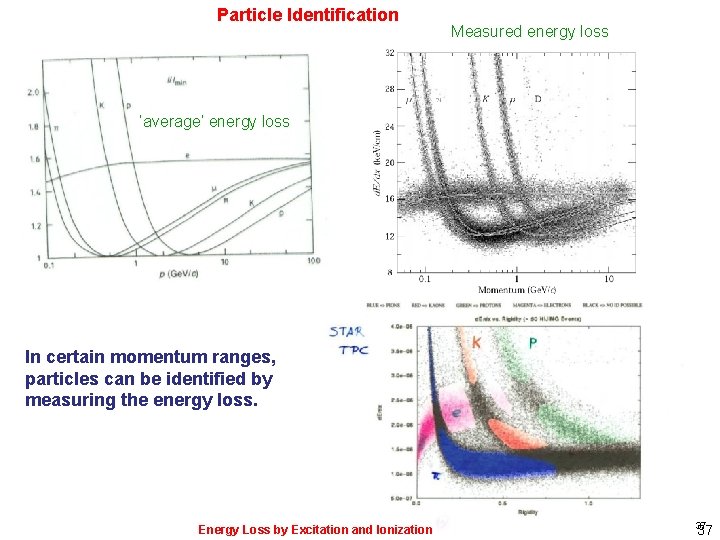
Particle Identification Measured energy loss ‘average’ energy loss In certain momentum ranges, particles can be identified by measuring the energy loss. Energy Loss by Excitation and Ionization 37 37

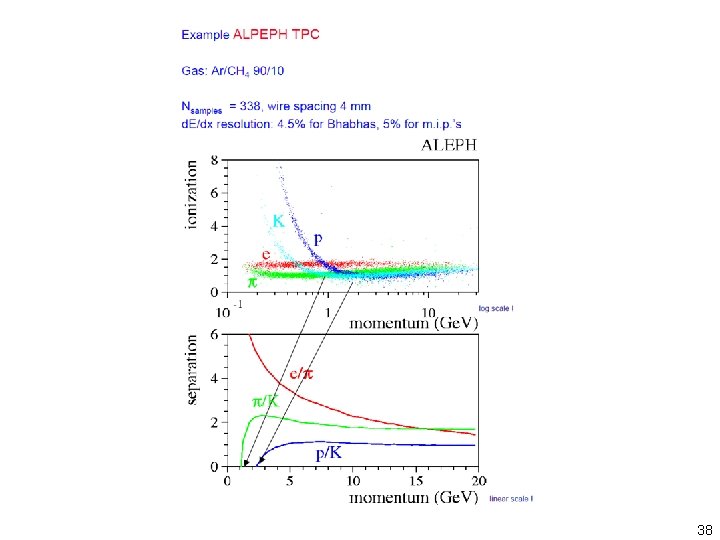
38

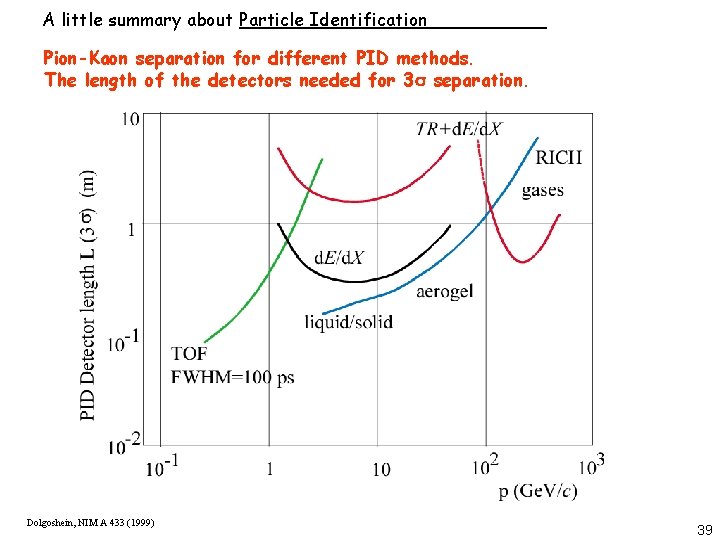
A little summary about Particle Identification Pion-Kaon separation for different PID methods. The length of the detectors needed for 3 s separation. Dolgoshein, NIM A 433 (1999) 39

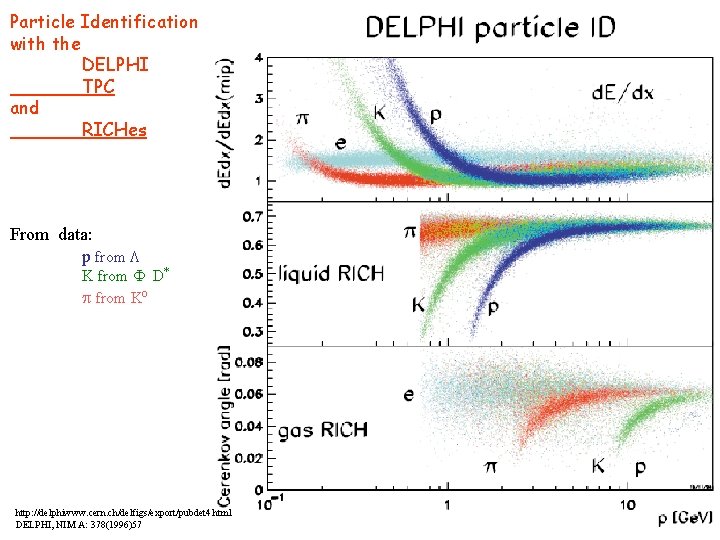
Particle Identification with the DELPHI TPC and RICHes From data: p from L K from F D* p from Ko http: //delphiwww. cern. ch/delfigs/export/pubdet 4. html DELPHI, NIM A: 378(1996)57 40

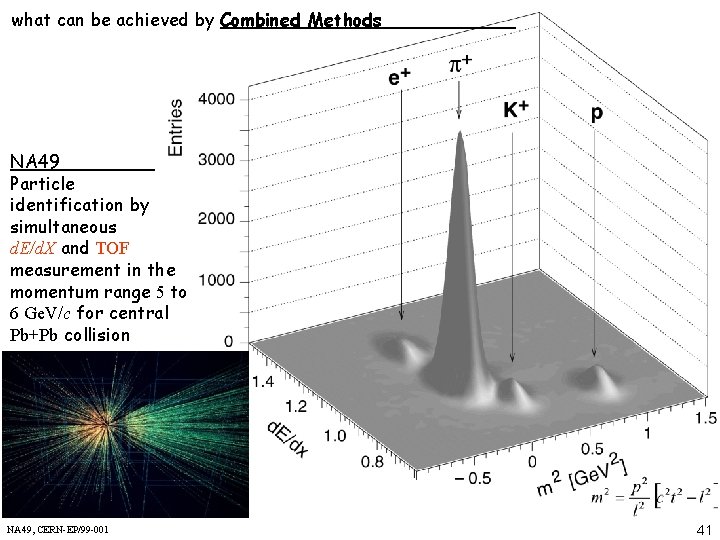
what can be achieved by Combined Methods NA 49 Particle identification by simultaneous d. E/d. X and TOF measurement in the momentum range 5 to 6 Ge. V/c for central Pb+Pb collision NA 49, CERN-EP/99 -001 41

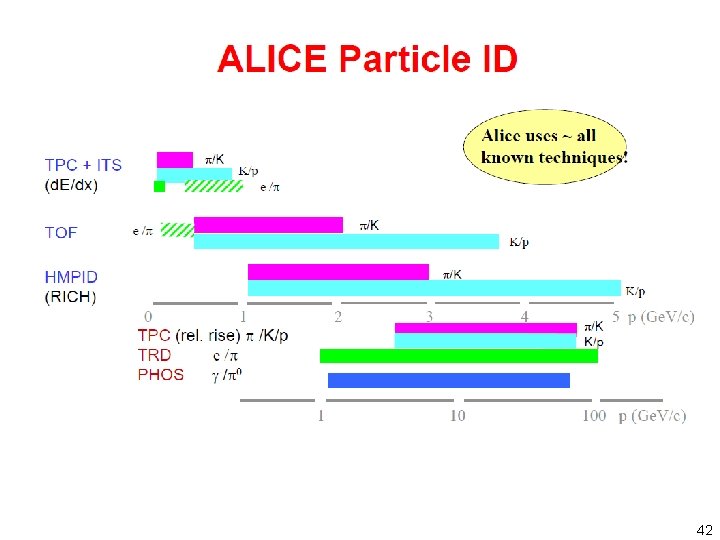
42

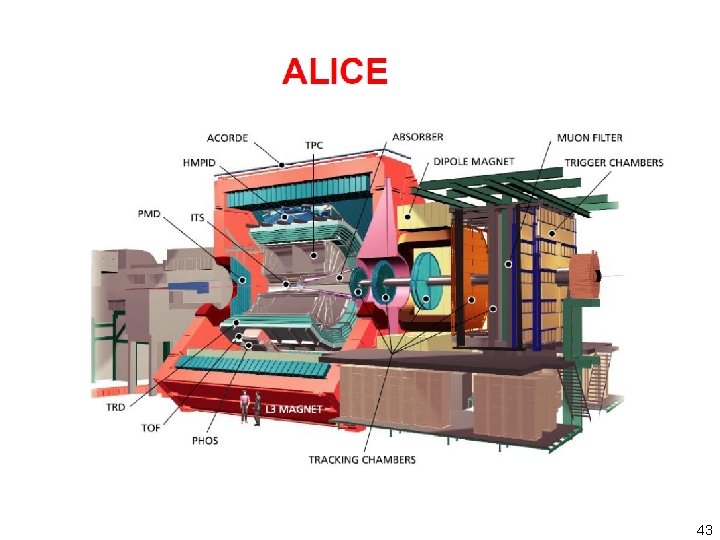
43

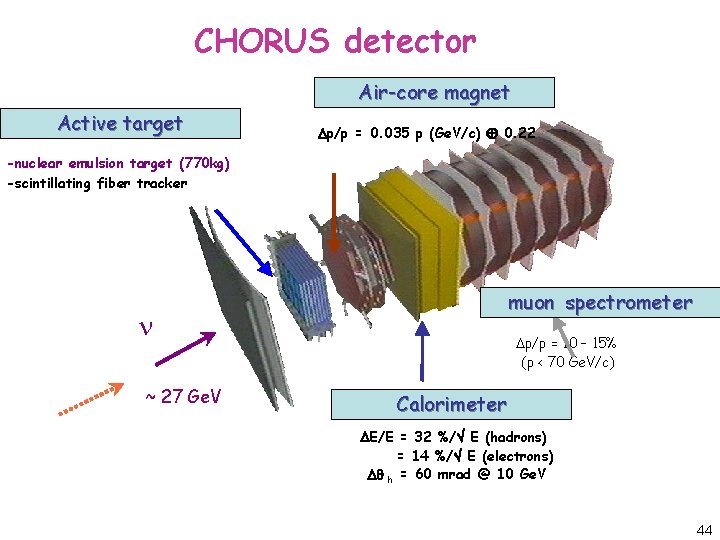
CHORUS detector Air-core magnet Active target p/p = 0. 035 p (Ge. V/c) 0. 22 -nuclear emulsion target (770 kg) -scintillating fiber tracker muon spectrometer ~ 27 Ge. V p/p = 10 – 15% (p < 70 Ge. V/c) Calorimeter E/E = 32 %/ E (hadrons) = 14 %/ E (electrons) h = 60 mrad @ 10 Ge. V 44

CHORUS detector T=5° Nucl. Instr. Meth A 401 (1997) 7 45

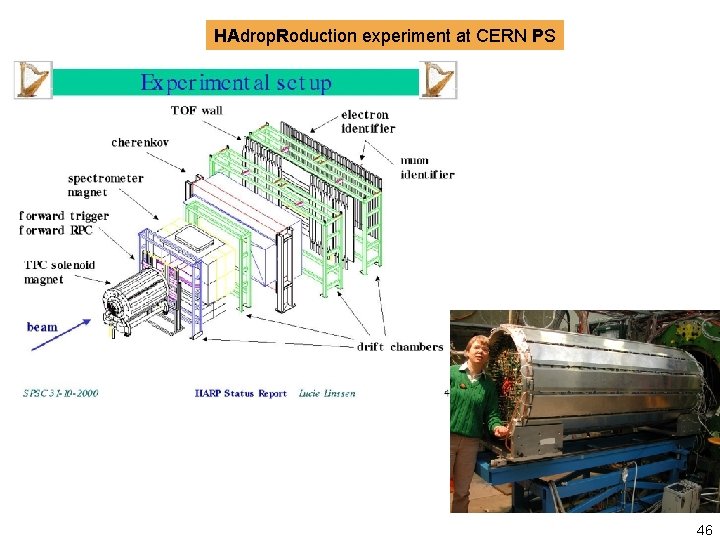
HAdrop. Roduction experiment at CERN PS 46

47




Изплозвани лекции от CERN Summer Student Program • Christian Joram 2001 • Olav Ullaland 2006 • Werner Riegler 2010 51