Particle Filters In Robotics or How the World
Particle Filters In Robotics or: How the World Became To Be One Big Bayes Network Sebastian Thrun Carnegie Mellon University of Pittsburgh
Robotics Research Today Particle Filters In Robotics 4 Open Problems Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Robotics Yesterday Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Robotics Today Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Robotics Tomorrow? Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Robotics Research Today Particle Filters In Robotics 4 Open Problems Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Robotics @ CMU, 1997 with W. Burgard, A. B. Cremers, D. Fox, D. Hähnel, G. Lakemeyer, D. Schulz, W. Steiner Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Robotics @ CMU, 1998 with M. Beetz, M. Bennewitz, W. Burgard, A. B. Cremers, F. Dellaert, D. Fox, D. Hähnel, C. Rosenberg, N. Roy, J. Schulte, D. Schulz Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
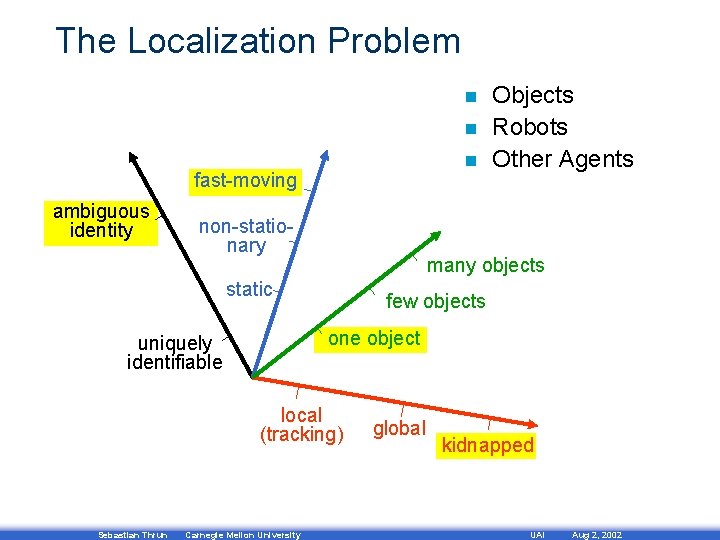
The Localization Problem n n n fast-moving ambiguous identity non-stationary many objects static few objects one object uniquely identifiable local (tracking) Sebastian Thrun Objects Robots Other Agents Carnegie Mellon University global kidnapped UAI Aug 2, 2002
Probabilistic Localization m map z 1 observations x 1 robot poses u 2 controls laser data Sebastian Thrun “Bayes filter” • HMMs z • DBNs 2 • POMDPs • Kalman filters x • 2 Particle filters x 3 • Condensation • etc z 3 . . . u 3 xt ut map m Carnegie Mellon University UAI Aug 2, 2002
![Bayes Filter Localization [Nourbakhsh et al 94] [Simmons/Koenig 95] [Kaelbling et al 96] Sebastian](http://slidetodoc.com/presentation_image_h2/6c2130a8c68f1ab6a596212e7b9e3e64/image-11.jpg "Bayes Filter Localization [Nourbakhsh et al 94] [Simmons/Koenig 95] [Kaelbling et al 96] Sebastian")
Bayes Filter Localization [Nourbakhsh et al 94] [Simmons/Koenig 95] [Kaelbling et al 96] Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
![What is the Right Representation? Kalman filter [Schiele et al. 94], [Weiß et al.](http://slidetodoc.com/presentation_image_h2/6c2130a8c68f1ab6a596212e7b9e3e64/image-12.jpg "What is the Right Representation? Kalman filter [Schiele et al. 94], [Weiß et al.")
What is the Right Representation? Kalman filter [Schiele et al. 94], [Weiß et al. 94], [Borenstein 96], [Gutmann et al. 96, 98], [Arras 98] Histograms (metric, topological) [Nourbakhsh et al. 95], [Simmons et al. 95], [Kaelbling et al. 96], [Burgard et al. 96], [Konolige et al. 99] Sebastian Thrun Carnegie Mellon University Multi-hypothesis [Weckesser et al. 98], [Jensfelt et al. 99] Particles [Kanazawa et al 95] [de Freitas 98] [Isard/Blake 98] [Doucet 98] UAI Aug 2, 2002
Particle Filters For Localization Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
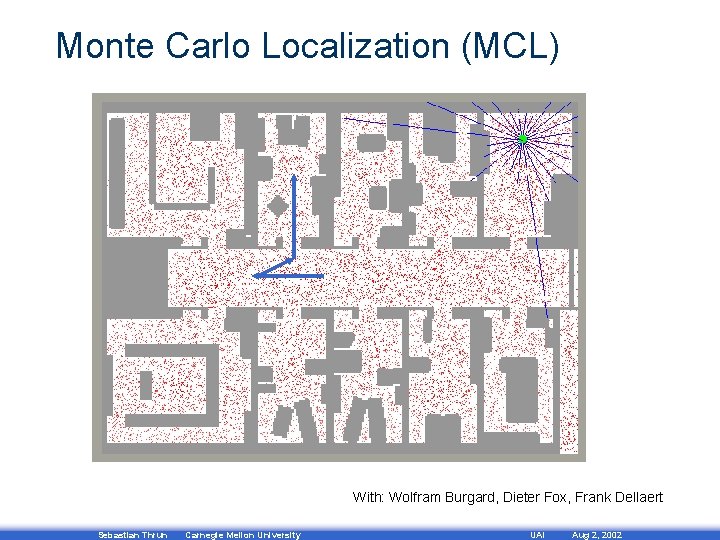
Monte Carlo Localization (MCL) With: Wolfram Burgard, Dieter Fox, Frank Dellaert Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Monte Carlo Localization With: Frank Dellaert Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Particle Filter in High Dimensions fast-moving ambiguous identity non-stationary many objects/features static few objects one object uniquely identifiable local (tracking) Sebastian Thrun Carnegie Mellon University global kidnapped UAI Aug 2, 2002
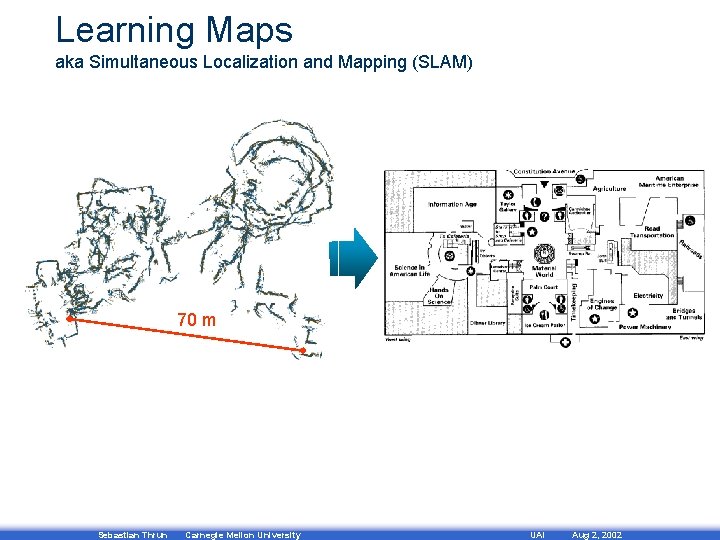
Learning Maps aka Simultaneous Localization and Mapping (SLAM) 70 m Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
The SLAM Problem Sebastian Thrun Carnegie Mellon University with known data association UAI Aug 2, 2002
![EKF Approach O(N 2) [Smith, Self, Cheeseman, 1985] Sebastian Thrun Carnegie Mellon University UAI](http://slidetodoc.com/presentation_image_h2/6c2130a8c68f1ab6a596212e7b9e3e64/image-21.jpg "EKF Approach O(N 2) [Smith, Self, Cheeseman, 1985] Sebastian Thrun Carnegie Mellon University UAI")
EKF Approach O(N 2) [Smith, Self, Cheeseman, 1985] Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Kalman Filter Mapping: O(N 2) Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
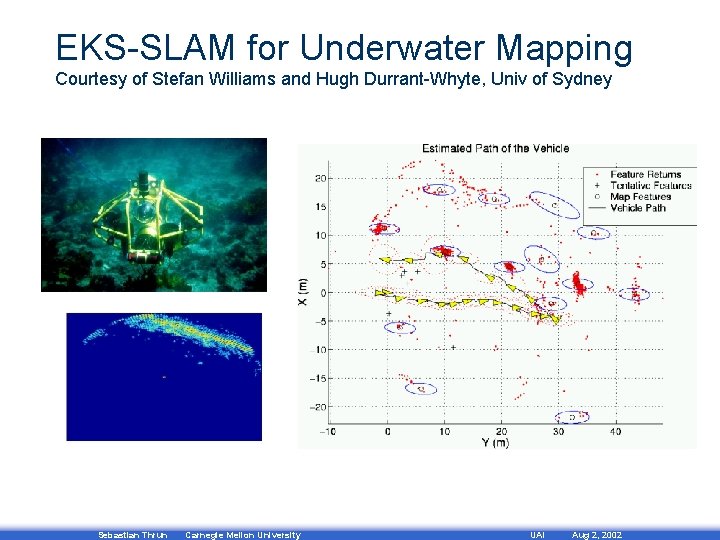
EKS-SLAM for Underwater Mapping Courtesy of Stefan Williams and Hugh Durrant-Whyte, Univ of Sydney Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Particle Filtering in Low Dimensions! sample pose robot poses Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Particle Filtering in High Dimensions? sample maps Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
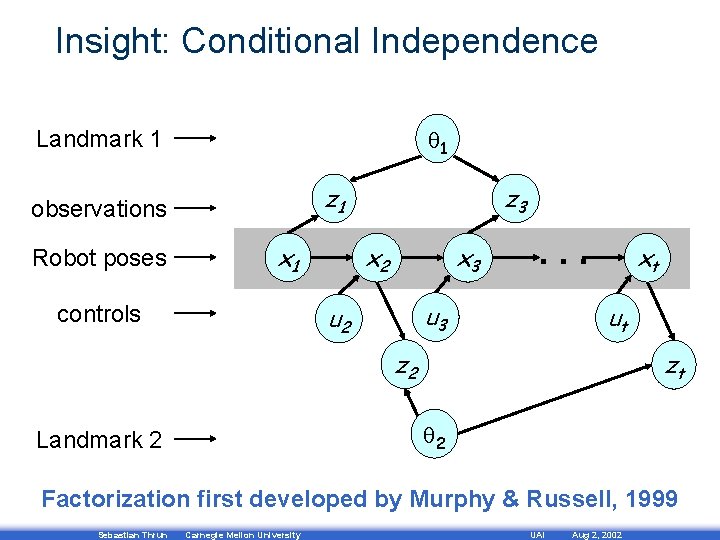
Insight: Conditional Independence 1 Landmark 1 z 1 observations Robot poses x 1 z 3 x 2 x 3 u 2 controls . . . xt ut z 2 zt 2 Landmark 2 Factorization first developed by Murphy & Russell, 1999 Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
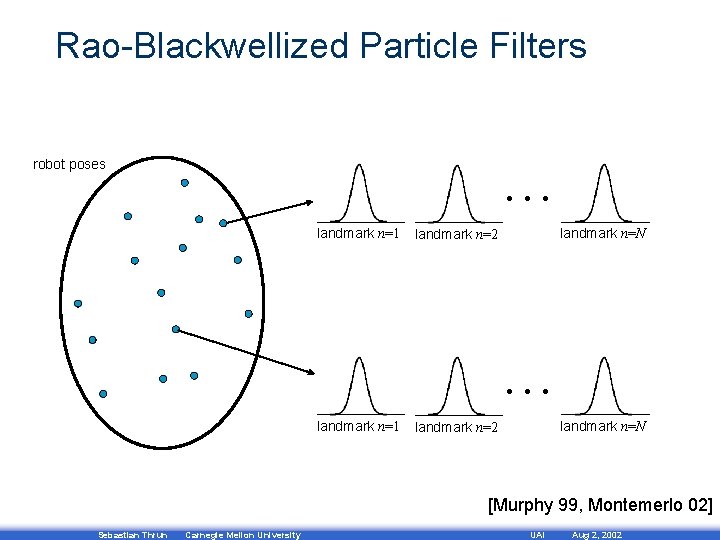
Rao-Blackwellized Particle Filters … robot poses landmark n=1 landmark n=N landmark n=2 … landmark n=1 landmark n=N landmark n=2 [Murphy 99, Montemerlo 02] Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
The Fast. SLAM Algorithm . 2. 7 Sebastian Thrun Carnegie Mellon University . 1 UAI Aug 2, 2002
Fast. SLAM - O(MN) n Update robot particles based on O(M) control ut Constant time per particle n Incorporate observation zt into Kalman filters n O(M) Constant time per particle Resample particle set O(MN) Linear time per particle M = Number of particles N = Number of map features Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
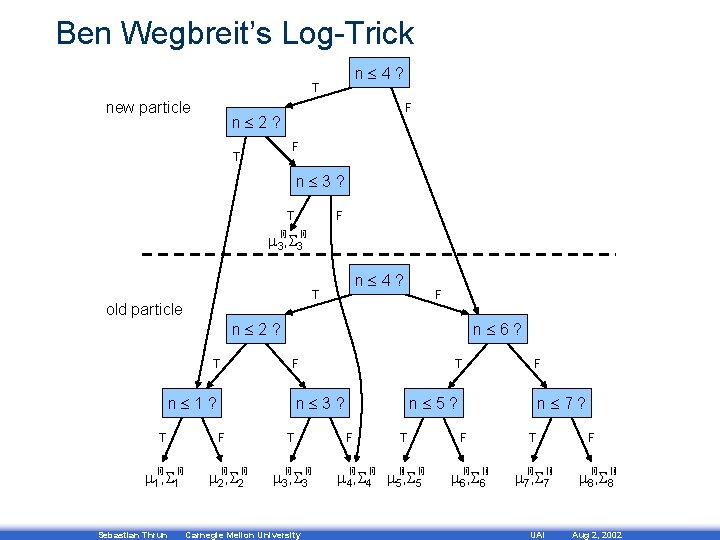
Ben Wegbreit’s Log-Trick n 4? T new particle F n 2? F T n 3? T F [i] m 3, S 3 old particle n k 6? F n k 1? [i] Sebastian Thrun T n k 3? F m 1, S 1 F n k 2? T T n k 4? T [i] m 2, S 2 [i] Carnegie Mellon University n k 1 5? F [i] m 3, S 3 F [i] T [i] n k 3 7? F [i] m 4, S 4 m 5, S 5 [i] T [i] m 6, S 6 [i] F [i] m 7, S 7 UAI [i] m 8, S 8 Aug 2, 2002
Fast. SLAM - O(M log. N) n n n Update robot particles based on control ut O(M) Constant time per particle Incorporate observation zt into Kalman filters Log time per particle Resample particle set O(M log. N) Log time per particle M = Number of particles N = Number of map features Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Advantage of Structured PF Solution Kalman: O(N 2) 500 features Fast. SLAM: O(Mlog. N) Moore’s Theorem: log. N 30 M: discussed later + global uncertainty, multi-modal + non-linear systems + sampling over data associations Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
3 Examples Particles + Kalman filters Particles + Point Estimators Particles + Particles Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Outdoor Mapping (no GPS) • 4 km excursion With Juan Nieto, Eduardo Nebot, Univ of Sydney Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
With Juan Nieto, Eduardo Nebot, Univ of Sydney Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
3 Examples Particles + Kalman filters Particles + Point Estimators Particles + Particles Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
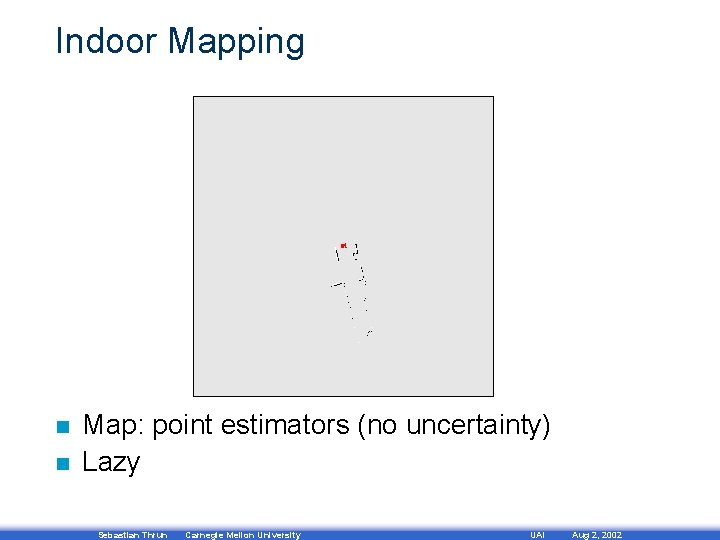
Indoor Mapping n n Map: point estimators (no uncertainty) Lazy Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
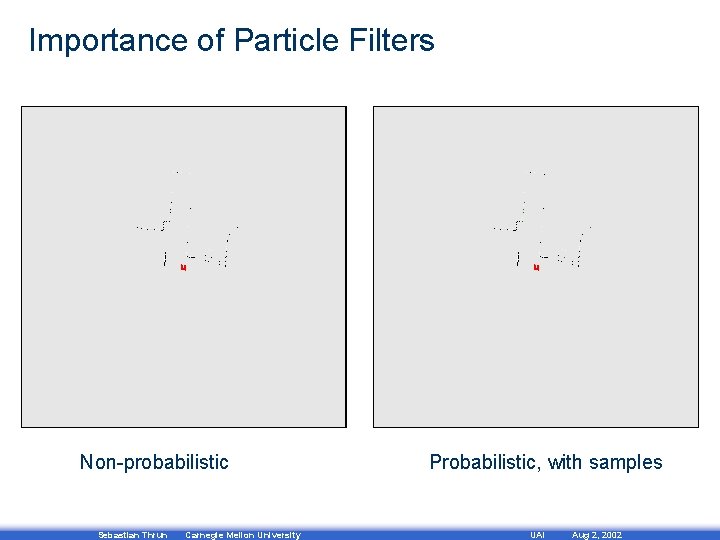
Importance of Particle Filters Non-probabilistic Sebastian Thrun Carnegie Mellon University Probabilistic, with samples UAI Aug 2, 2002
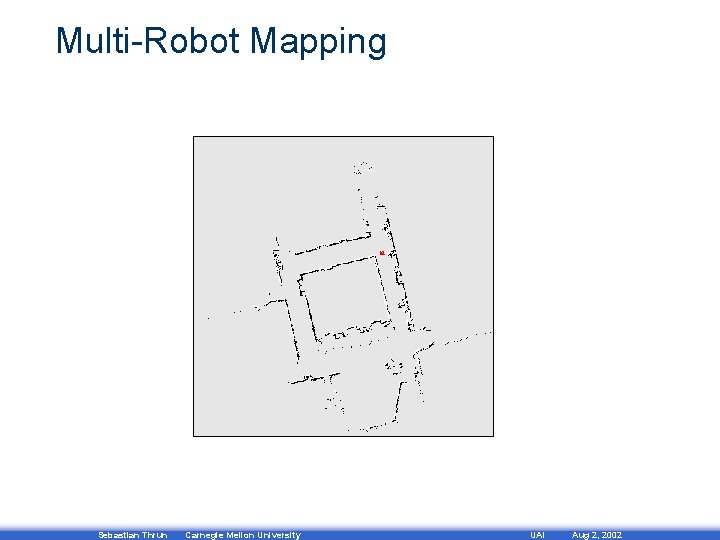
Multi-Robot Mapping Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Multi-Robot Exploration DARPA TMR Texas DARPA TMR Maryland With: Reid Simmons and Dieter Fox Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
3 Examples Particles + Kalman filters Particles + Point Estimators Particles + Particles Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Tracking Moving Features With: Michael Montemerlo Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
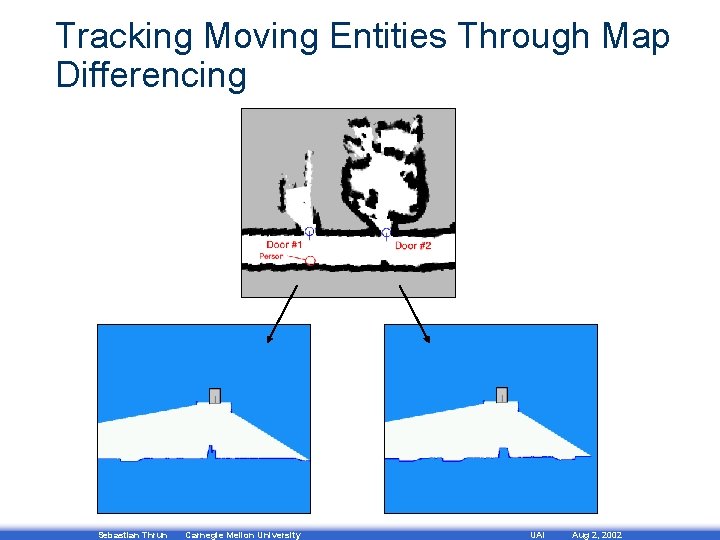
Tracking Moving Entities Through Map Differencing Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Map-Based People Tracking With: Michael Montemerlo Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
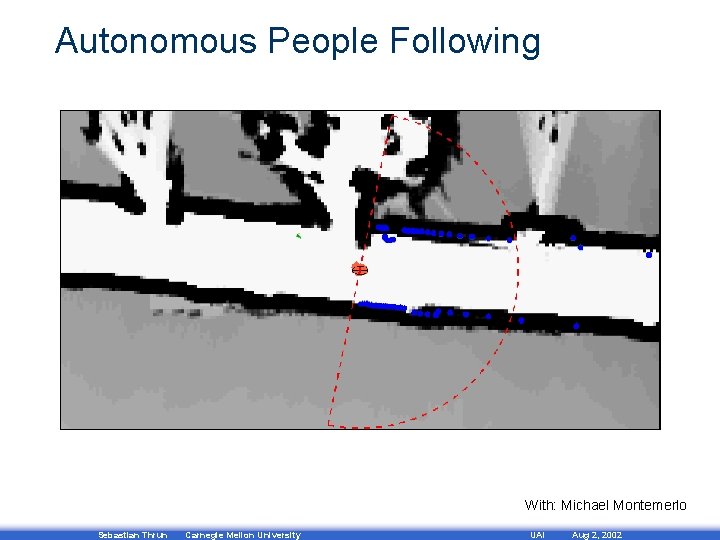
Autonomous People Following With: Michael Montemerlo Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Advantage of Structured PF Solution Kalman: O(N 2) 500 features Fast. SLAM: O(Mlog. N) Moore’s Theorem: log. N 30 M: discussed now! + global uncertainty, multi-modal + non-linear systems + sampling over data associations Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
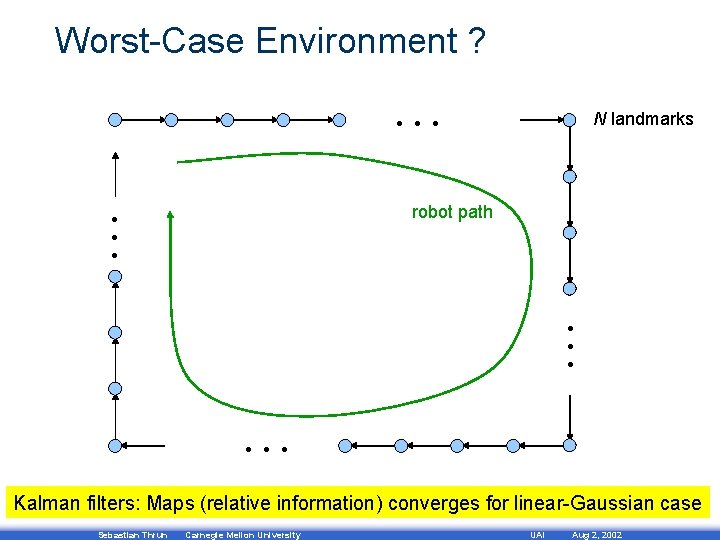
Worst-Case Environment ? … N landmarks … robot path … … Kalman filters: Maps (relative information) converges for linear-Gaussian case Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
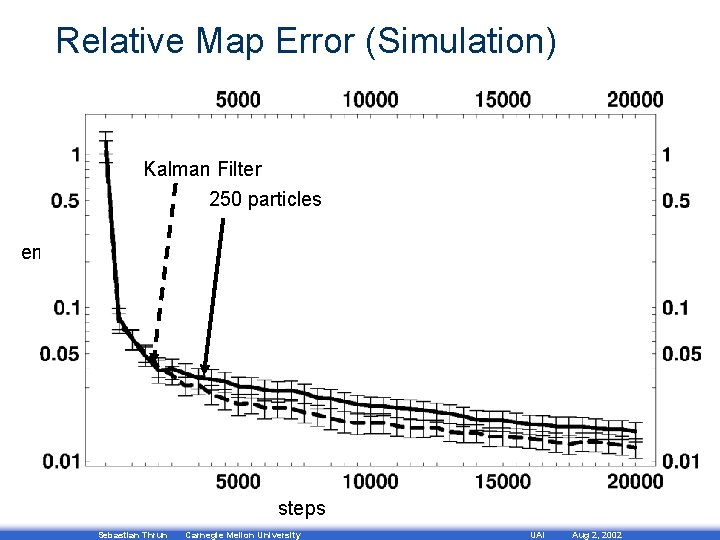
Relative Map Error (Simulation) Kalman Filter 250 particles error steps Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
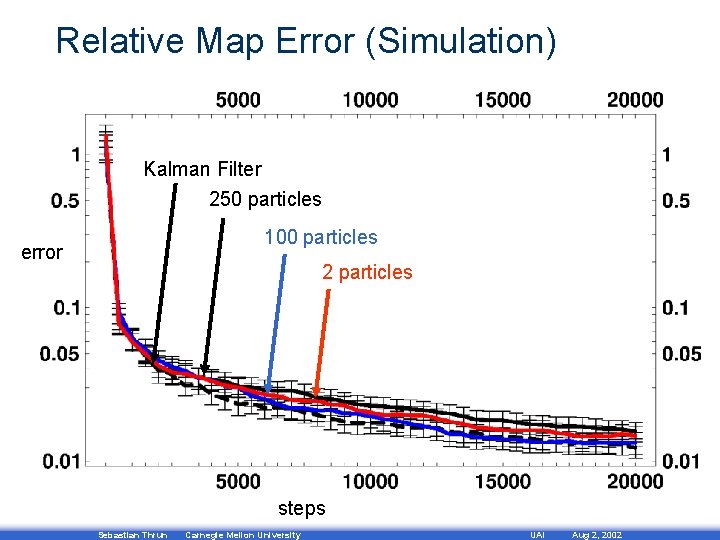
Relative Map Error (Simulation) Kalman Filter 250 particles 100 particles error 2 particles steps Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
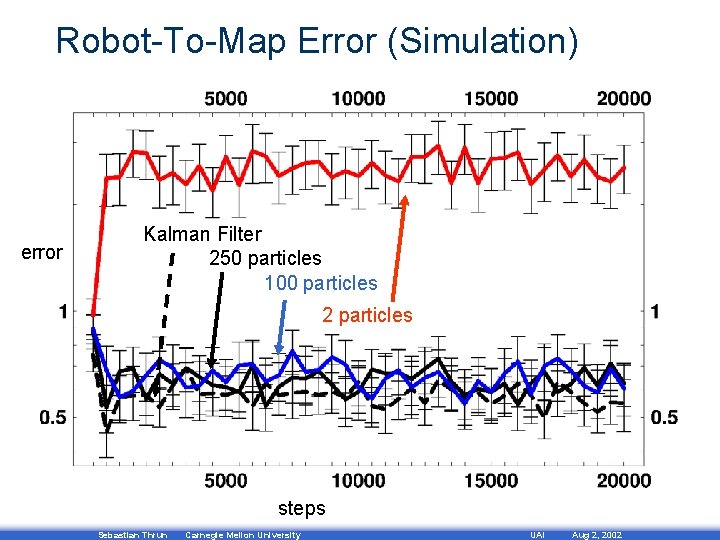
Robot-To-Map Error (Simulation) error Kalman Filter 250 particles 100 particles 2 particles steps Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Summary Results n O(N 2) O(MN) O(M log. N) O(log. N) O(N 2) O(log. N) n Scalable(? ) solution to data association problem Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Robotics Research Today Particle Filters In Robotics 4 Open Problems Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Can We Factorize Better? Static Factorization Dynamic Factorization Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
![Example: Multi-Robot Localization [Fox et al, 99] Sebastian Thrun Carnegie Mellon University UAI Aug](http://slidetodoc.com/presentation_image_h2/6c2130a8c68f1ab6a596212e7b9e3e64/image-54.jpg "Example: Multi-Robot Localization [Fox et al, 99] Sebastian Thrun Carnegie Mellon University UAI Aug")
Example: Multi-Robot Localization [Fox et al, 99] Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
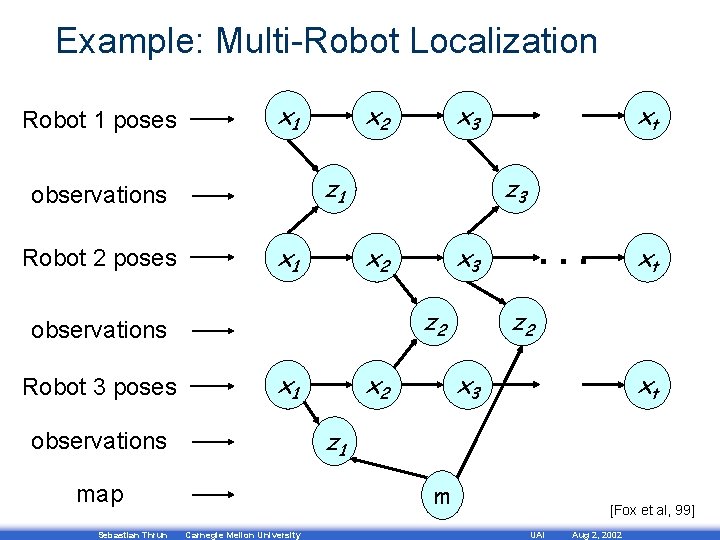
Example: Multi-Robot Localization Robot 1 poses x 1 x 2 xt z 2 x 3 xt z 1 observations m map Sebastian Thrun . . . x 3 z 2 x 1 xt z 3 observations Robot 3 poses x 3 z 1 observations Robot 2 poses x 2 Carnegie Mellon University [Fox et al, 99] UAI Aug 2, 2002
![Dynamic Factorization ? ? Task: calculate E[y|x] from samples error Robot y always use](http://slidetodoc.com/presentation_image_h2/6c2130a8c68f1ab6a596212e7b9e3e64/image-56.jpg "Dynamic Factorization ? ? Task: calculate E[y|x] from samples error Robot y always use")
Dynamic Factorization ? ? Task: calculate E[y|x] from samples error Robot y always use joint always factorize dynamically optimal # samples Robot x Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Can We Learn Control? n n Not an MDP Not discrete or low-dimensional Not knowledge-free Only thing that matters in robotics Sondik 71, Littman/Kaelbling/Cassandra 96, … Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
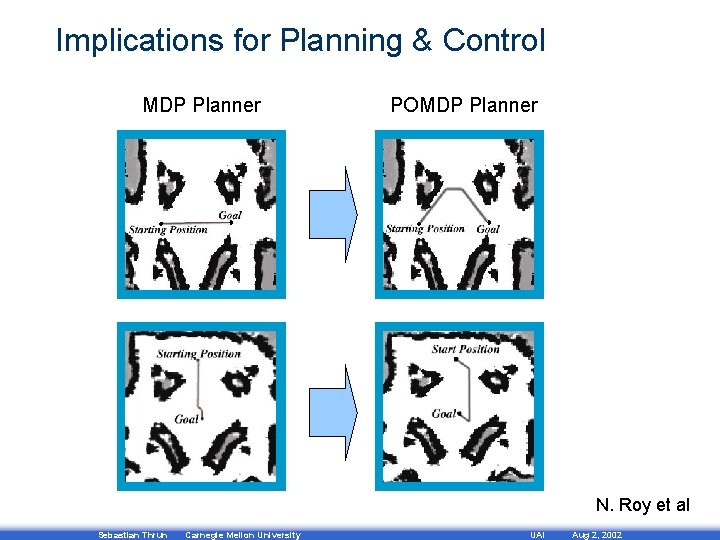
Implications for Planning & Control MDP Planner POMDP Planner N. Roy et al Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Can we Exploit Procedural Knowledge? Programming Learning prob<int> See Davidx. Andre’s = {{10, 0. 2}, and Stuart {11, 0. 8}}; Russell’s AAAI paper prob<int> y =this {{20, year! 0. 5}, {21, 0. 5}}; prob<int> z = x + y; prob<double> f = neuro. Net(y); with Frank Pfenning, CMU Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
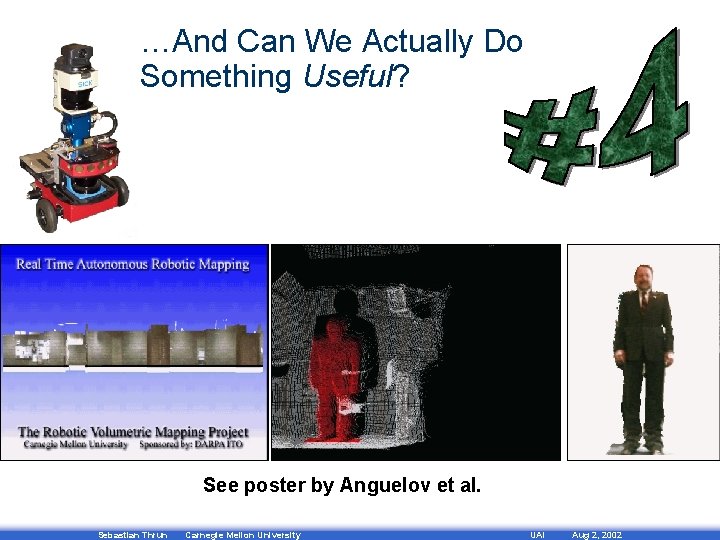
…And Can We Actually Do Something Useful? See poster by Anguelov et al. Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
The Nursebot Project University of Pittsburgh School of Nursing Prof. Jackie Dunbar-Jacob Prof. Sandy Engberg Prof. Margo Holm Prof. Deb Lewis Prof. Judy Matthews Prof. Barbara Spier School of Medicine Prof. Neil Resnick Prof. Joan Rogers Intelligent Systems Prof. Don Chiarulli University of Pittsburgh Computer Science Prof. Martha Pollack Carnegie Mellon University Computer Science, Robotics Prof. Sebastian Thrun Prof. Geoff Gordon Human Computer Interaction Prof. Sara Kiesler Financial Support National Science Foundation $1. 4 M ITR Grant $3. 2 M ITR Grant Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
The Nursebot Project Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Haptic Interface (In Development) Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
Wizard of Oz Studies By Sara Kiesler, Jenn Goetz Sebastian Thrun Carnegie Mellon University UAI Aug 2, 2002
- Slides: 64