Particle Filtering Sensors and Uncertainty Real world sensors

Particle Filtering

Sensors and Uncertainty • Real world sensors are noisy and suffer from missing data (e. g. , occlusions, GPS blackouts) • Use dynamics models and sensor models to estimate ground truth, unobserved variables, make forecasts, fuse multiple sensors

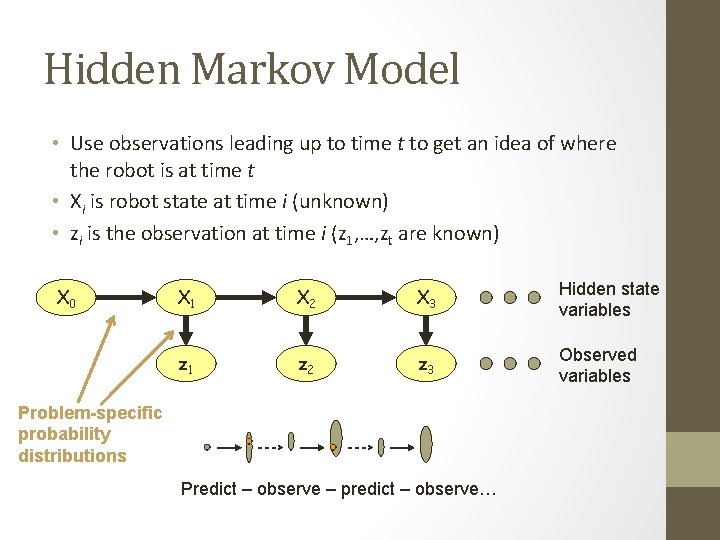
Hidden Markov Model • Use observations leading up to time t to get an idea of where the robot is at time t • Xi is robot state at time i (unknown) • zi is the observation at time i (z 1, …, zt are known) X 0 X 1 X 2 X 3 Hidden state variables z 1 z 2 z 3 Observed variables Problem-specific probability distributions Predict – observe – predict – observe…

Last Class • Kalman Filtering and its extensions • Exact Bayesian inference for Gaussian state distributions, process noise, observation noise • What about more general distributions? • Key representational issue • How to represent and perform calculations on probability distributions?

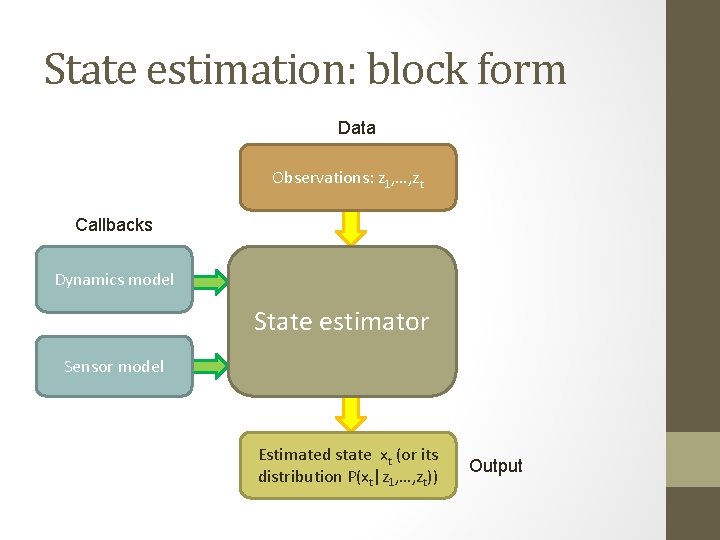
State estimation: block form Data Observations: z 1, …, zt Callbacks Dynamics model State estimator Sensor model Estimated state xt (or its distribution P(xt|z 1, …, zt)) Output

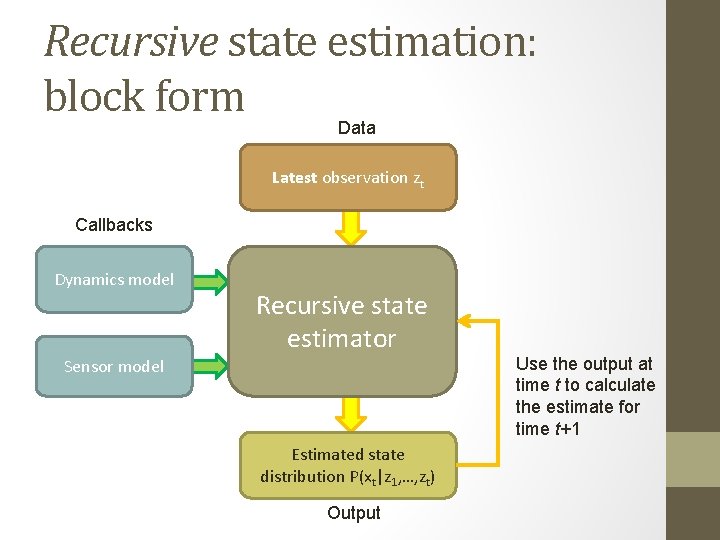
Recursive state estimation: block form Data Latest observation zt Callbacks Dynamics model Recursive state estimator Sensor model Estimated state distribution P(xt|z 1, …, zt) Output Use the output at time t to calculate the estimate for time t+1

Particle Filtering (aka Sequential Monte Carlo) • Represent distributions as a set of particles • Applicable to non-gaussian high-D distributions • Convenient implementations • Widely used in vision, robotics

Simultaneous Localization and Mapping (SLAM) • Mobile robots • Odometry • Locally accurate • Drifts significantly over time • Vision/ladar/sonar • Inaccurate locally • Global reference frame • Combine the two • State: (robot pose, map) • Observations: (sensor input)

General problem • xt ~ Bel(xt) (arbitrary p. d. f. ) [Dynamics model] • xt+1 = f(xt, u, ep) Process noise [Sensor model] • zt+1 = g(xt+1, eo) Observation noise • ep ~ arbitrary p. d. f. , eo ~ arbitrary p. d. f.

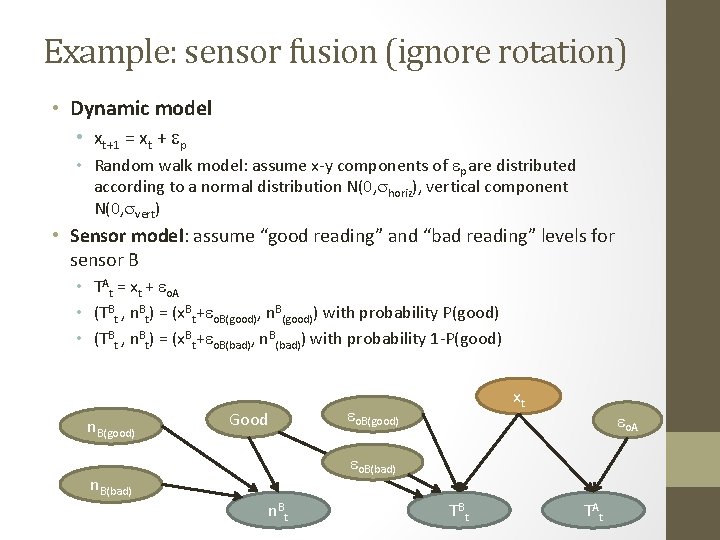
Example: sensor fusion • Two sensors estimate an underlying process, e. g. , pose estimation • State: position + orientation of frame • Sensor A: Inertial measurement unit • Sensor B: visual odometry, feature tracking • Sensor A is more noisy on average but is consistent • Sensor B is accurate most of the time but has occasional failures • State Xt: true pose at time t • Observation zt: (TAt, TBt, n. Bt) with n. Bt = # of feature matches in visual odometry between frames t and t-1

Example: sensor fusion (ignore rotation) • Dynamic model • xt+1 = xt + ep • Random walk model: assume x-y components of ep are distributed according to a normal distribution N(0, shoriz), vertical component N(0, svert) • Sensor model: assume “good reading” and “bad reading” levels for sensor B • TAt = xt + eo. A • (TBt , n. Bt) = (x. Bt+eo. B(good), n. B(good)) with probability P(good) • (TBt , n. Bt) = (x. Bt+eo. B(bad), n. B(bad)) with probability 1 -P(good) n. B(good) Good xt eo. B(good) eo. A eo. B(bad) n. B t TA t

Particle Representation • • Bel(xt) = {(wk, xk), k=1, …, n} wk are weights, xk are state hypotheses Weights sum to 1 Approximates the underlying distribution

Monte Carlo Integration • If P(x) ≈ Bel(x) = {(wk, xk), k=1, …, N} • EP[f(x)] = integral[ f(x)P(x)dx ] ≈ Sk wk f(xk) • What might you want to compute? • Mean: set f(x) = x • Variance: f(x) = x 2 (recover Var(x) = E[x 2]-E[x]2) • P(y): set f(x) = P(y|x) • Because P(y) = integral[ P(y|x)P(x)dx ]

Filtering Steps • Predict • Compute Bel’(xt+1): distribution of xt+1 using dynamics model alone • Update • Compute a representation of P(xt+1|zt+1) via likelihood weighting for each particle in Bel’(xt+1) • Resample to produce Bel(xt+1) for next step

Predict Step • Given input particles Bel(xt) • Distribution of xt+1=f(xt, ut, e) determined by sampling e from its distribution and then propagating individual particles • Gives Bel’(xt+1)

Particle Propagation

Update Step • Goal: compute a representation of P(xt+1 | zt+1) given Bel’(xt+1), zt+1 • P(xt+1 | zt+1) = a P(zt+1 | xt+1) P(xt+1) • P(xt+1) = Bel’(xt+1) (given) • Each state hypothesis xk Bel’(xt+1) is reweighted by P(zt+1 | xt+1) • Likelihood weighting: • wk P(zt+1|xt+1=xk) • Then renormalize to 1

Update Step • wk wk’ * P(zt+1 | xt+1=xk) • 1 D example: • g(x, eo) = h(x) + eo • eo ~ N(m, s) • P(zt+1 | xt+1=xk) = C exp(- (h(xk)-zt+1)2 / 2 s 2) • In general, distribution can be calibrated using experimental data

Resampling • Likelihood weighted particles may no longer represent the distribution efficiently • Importance resampling: sample new particles proportionally to weight

Sampling Importance Resampling (SIR) variant Predict Update Resample

Particle Filtering Issues • Variance • Std. dev. of a quantity (e. g. , mean) computed as a function of the particle representation ~ 1/sqrt(N) • Loss of particle diversity • Resampling will likely drop particles with low likelihood • They may turn out to be useful hypotheses in the future

Other Resampling Variants • Selective resampling • Keep weights, only resample when # of “effective particles” < threshold • Stratified resampling • Reduce variance using quasi-random sampling • Optimization • Explicitly choose particles to minimize deviance from posterior • …

Storing more information with same # of particles • Unscented Particle Filter • Each particle represents a local gaussian, maintains a local covariance matrix • Combination of particle filter + Kalman filter • Rao-Blackwellized Particle Filter • State (x 1, x 2) • Particle contains hypothesis of x 1, analytical distribution over x 2 • Reduces variance

Advanced Filtering Topics • Mixing exact and approximate representations (e. g. , mixture models) • Multiple hypothesis tracking (assignment problem) • Model calibration • Scaling up (e. g. , 3 D SLAM, huge maps)

Recap • Bayesian mechanisms for state estimation are well understood • Representation challenge • Methods: • Kalman filters: highly efficient closed-form solution for Gaussian distributions • Particle filters: approximate filtering for high-D, non. Gaussian distributions • Implementation challenges for different domains (localization, mapping, SLAM, tracking)

Project presentations • 5 minutes each • Suggested format Slide 1: Project title, team members Slide 2: Motivation, problem overview Slide 3: Demonstration scenario walkthrough. Include figures. Slide 4: Breakdown of system components, team member roles. System block diagram. • Slide 5: Integration plan. Identify potential issues to monitor • • • Integration plan • 3 -4 milestones (1 -2 weeks each) • Make sure you still have a viable proof-of-concept demo if you cannot complete final milestone • Take feedback into account in 2 page project proposal doc. • Due 3/26, but you should start on work plan ASAP.

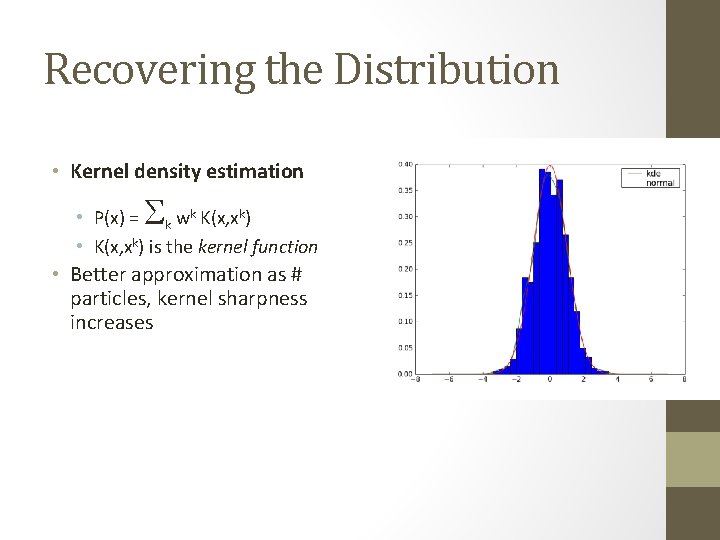
Recovering the Distribution • Kernel density estimation S • P(x) = k wk K(x, xk) • K(x, xk) is the kernel function • Better approximation as # particles, kernel sharpness increases