Particle Filtering ICS 275 b 2002 Dynamic Belief

Particle Filtering ICS 275 b 2002

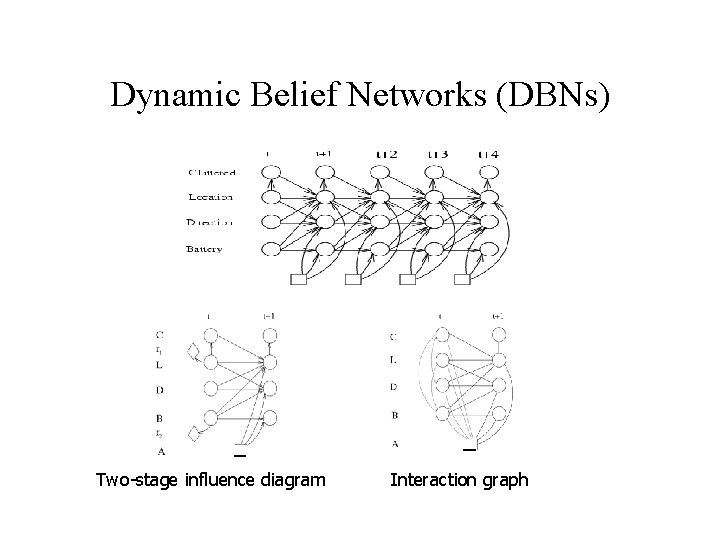
Dynamic Belief Networks (DBNs) Two-stage influence diagram Interaction graph

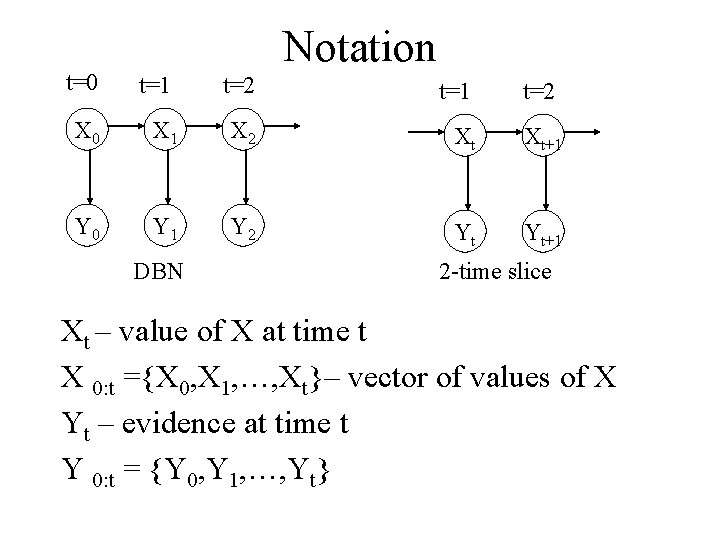
Notation t=0 t=1 t=2 X 0 X 1 X 2 Xt Xt+1 Y 0 Y 1 Y 2 Yt Yt+1 DBN 2 -time slice Xt – value of X at time t X 0: t ={X 0, X 1, …, Xt}– vector of values of X Yt – evidence at time t Y 0: t = {Y 0, Y 1, …, Yt}

Query • Compute P(X 0: t |Y 0: t ) or P(X t |Y 0: t ) • Hard!!! over a long time period • Approximate! Sample!

Particle Filtering (PF) • = “condensation” • = “sequential Monte Carlo” • = “survival of the fittest” – PF can treat any type of probability distribution, non-linearity, and non-stationarity; – PF are powerful sampling based inference/learning algorithms for DBNs.

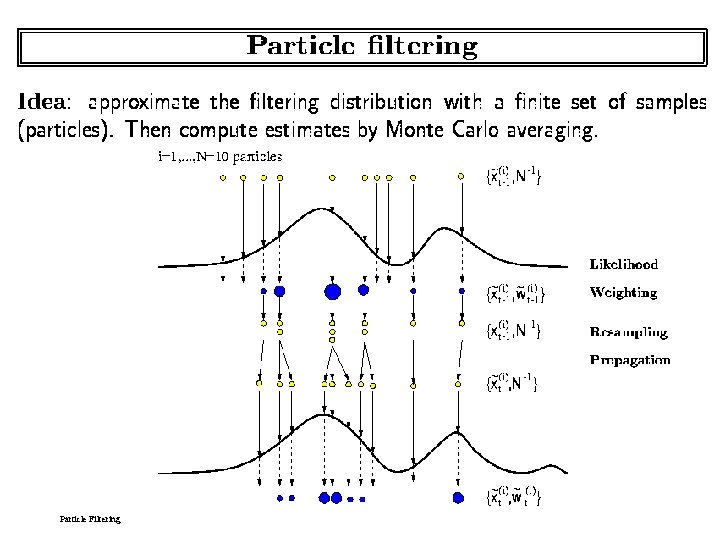
Particle Filtering

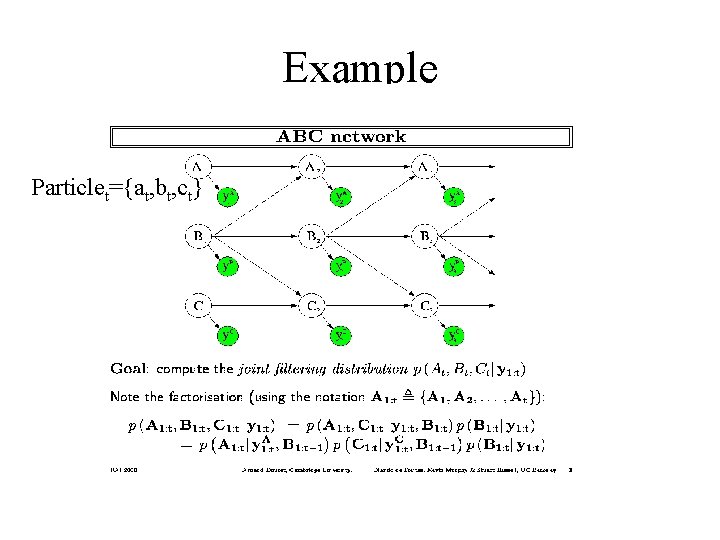
Example Particlet={at, bt, ct}

PF Sampling Particle (t) ={at, bt, ct} Compute particle (t+1): Sample bt+1, from P(b|at, ct) Sample at+1, from P(a|bt+1, ct) Sample ct+1, from P(c|bt+1, at+1) Weight particle wt+1 If weight is too small, discard Otherwise, multiply

Drawback of PF • Drawback of PF – Inefficient in high-dimensional spaces (Variance becomes so large) • Solution – Rao-Balckwellisation, that is, sample a subset of the variables allowing the remainder to be integrated out exactly. The resulting estimates can be shown to have lower variance. • Rao-Blackwell Theorem

Problem Formulation • Model : general state space model/DBN with hidden variables zt and observed variables yt • Objective: – or filtering density – To solve this problem, one need approximation schemes because of intractable integrals

Rao-Blackwellised PF Divide hidden variables into two groups: rt and xt • Assume conditional posterior distribution p(x 0: t | y 1: t , r 0: t , ) is analytically tractable • We only need to focus on estimating p(r 0: t | y 1: t), which lies in a space of reduced dimension:

Particle Filtering and Rao. Blackwellisation • Monte Carlo integration