Partial ionization of hydrogen plasma in the solar

Partial ionization of hydrogen plasma in the solar atmosphere Non-LTE modeler’s view P. Heinzel Astronomical Institute, Czech Academy of Sciences

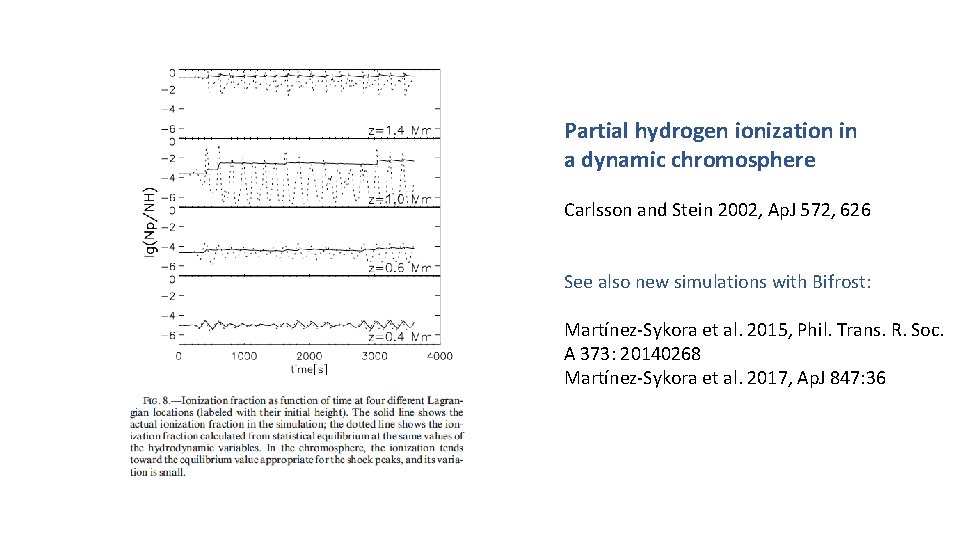
Partial hydrogen ionization in a dynamic chromosphere Carlsson and Stein 2002, Ap. J 572, 626 See also new simulations with Bifrost: Martínez-Sykora et al. 2015, Phil. Trans. R. Soc. A 373: 20140268 Martínez-Sykora et al. 2017, Ap. J 847: 36

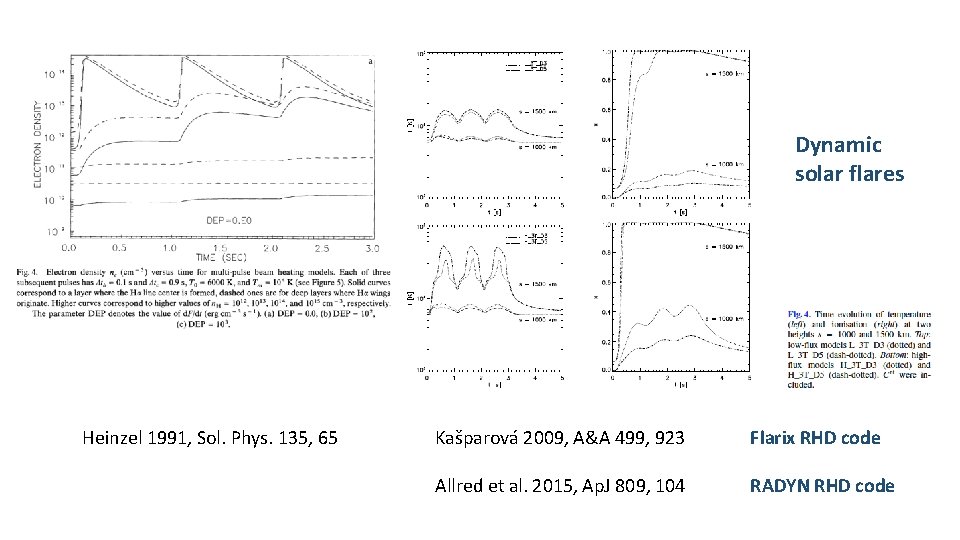
Dynamic solar flares Heinzel 1991, Sol. Phys. 135, 65 Kašparová 2009, A&A 499, 923 Flarix RHD code Allred et al. 2015, Ap. J 809, 104 RADYN RHD code

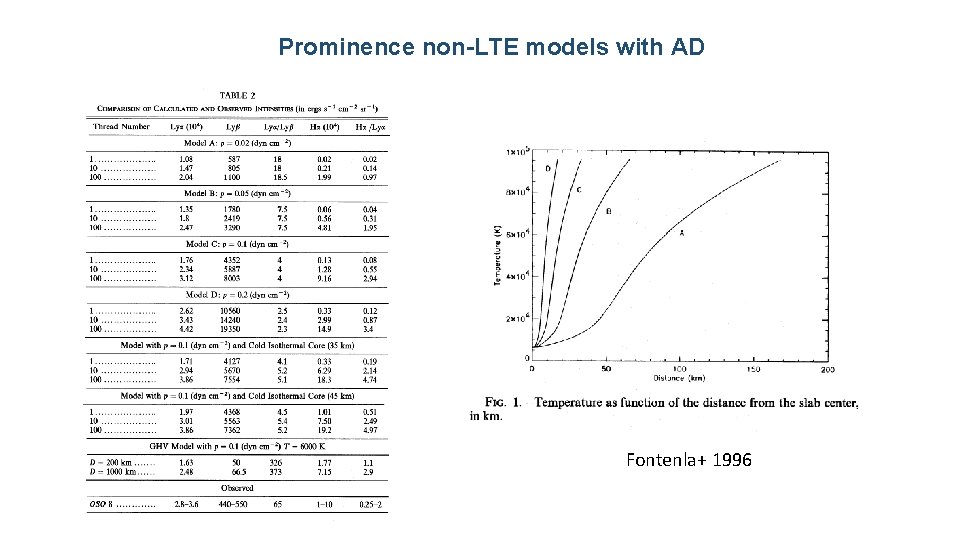
Prominence non-LTE models with AD Fontenla+ 1996

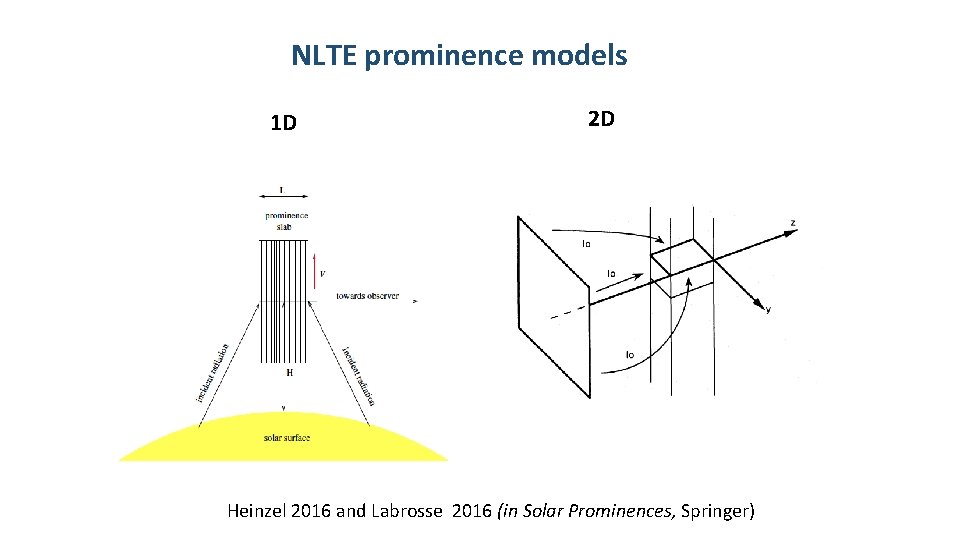
NLTE prominence models 1 D 2 D Heinzel 2016 and Labrosse 2016 (in Solar Prominences, Springer)

MALI NLTE transfer code • 1 D/2 D-slab geometry (MALI 1 D/MALI 2 D) – Heinzel 2016 • isothermal-isobaric slabs, generalization to PCTR • height-velocity dependent radiative boundary conditions (including photoionization by external radiation) • multilevel hydrogen atom with continuum (ionization) • other species like Ca. II and Mg. II • coupled radiative transfer + statistical equilibrium • fast numerical solution using the ALI techniques • Non-equilibrium ionization of hydrogen with the MALI code

NLTE modeling of partial hydrogen ionization • Input: T, p, D, vnt , H, vflow • Output: ne , n. HI , radiative and collisional rates, relaxation times • Prominence or a CME-core is approximated by a 1 D/2 D slab models (L-alpha line is optically very thick in prominences, mostly thin in CMEs) • We solve the radiative transfer and statistical-equilibrium equations for a 5 -level + continuum hydrogen atom

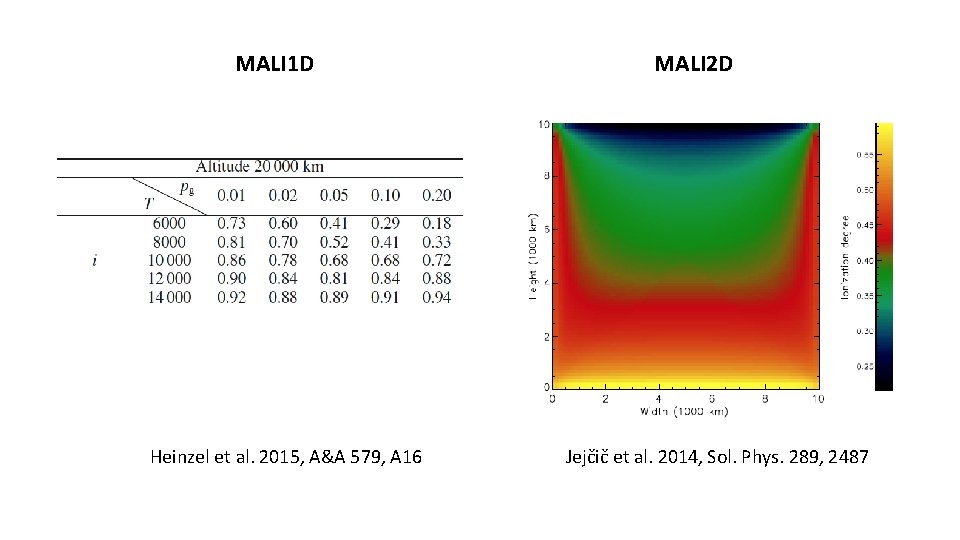
MALI 1 D Heinzel et al. 2015, A&A 579, A 16 MALI 2 D Jejčič et al. 2014, Sol. Phys. 289, 2487

Grid of models from cool eruptive prominences to hotter CME cores • T-range: 10 000 – 100 000 K • p-range: 0. 001 – 1. 0 dyn cm-2 • D: 5000 and 50 000 km • vt : 5 km s-1 • H: 350 000 km • zero flow velocity (no Doppler effects in the continua) Heinzel and Jejčič 2019, in preparation

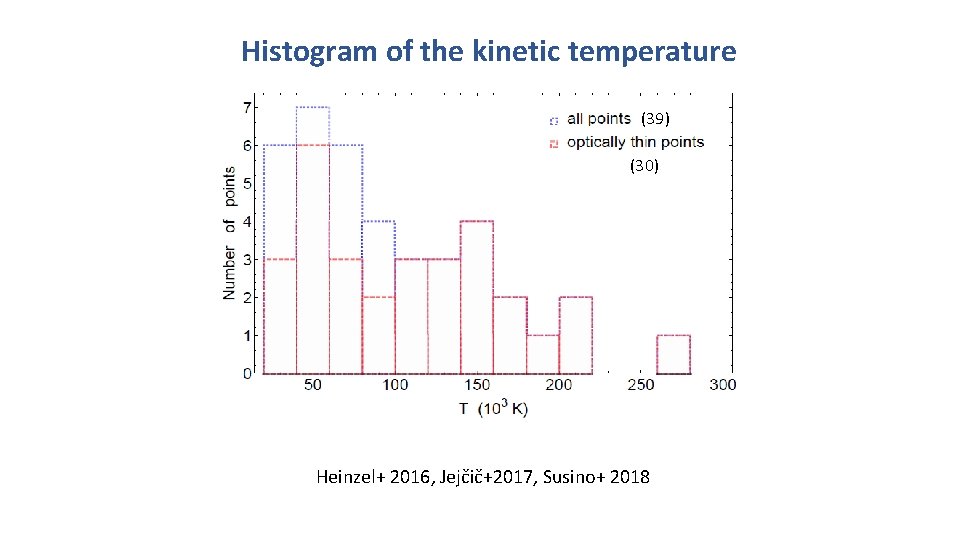
Histogram of the kinetic temperature (39) (30) Heinzel+ 2016, Jejčič+2017, Susino+ 2018

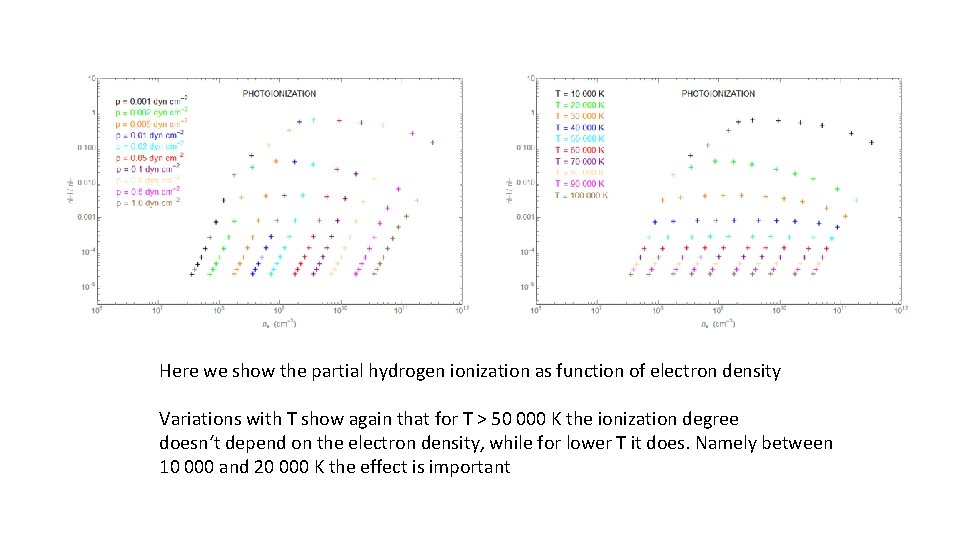
Photoionization is negligible for T > 50 000 K, where hydrogen ionization equilibrium is consistent with CHIANTI or Arnaud & Rothenflug (1985); depends only on T For T < 50 000 K, photoionization starts to be important, and namely at low T between 10 000 – 30 000 K where the situation becomes very complex

Here we show the partial hydrogen ionization as function of electron density Variations with T show again that for T > 50 000 K the ionization degree doesn‘t depend on the electron density, while for lower T it does. Namely between 10 000 and 20 000 K the effect is important

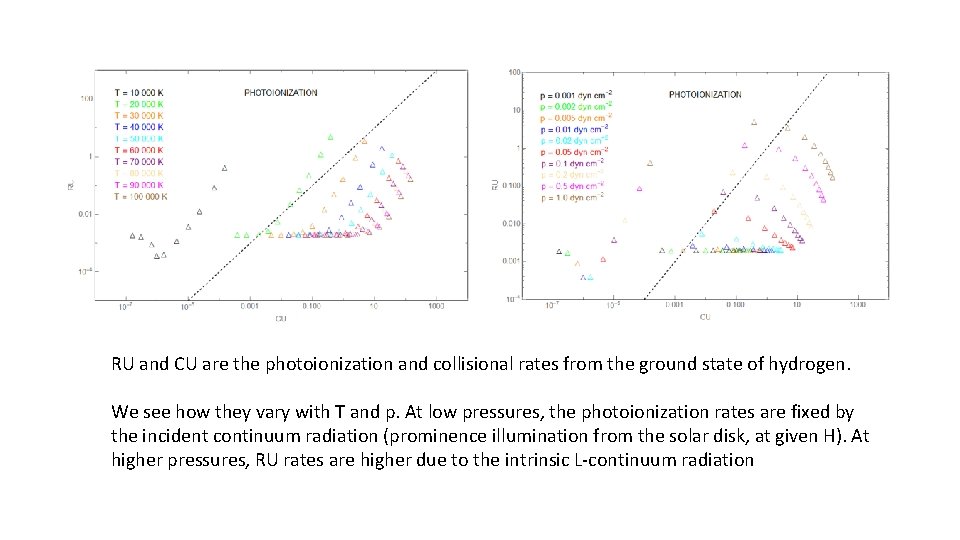
RU and CU are the photoionization and collisional rates from the ground state of hydrogen. We see how they vary with T and p. At low pressures, the photoionization rates are fixed by the incident continuum radiation (prominence illumination from the solar disk, at given H). At higher pressures, RU rates are higher due to the intrinsic L-continuum radiation

Kinetic equilibrium for processes 1 <-> k (in general we have 5 eqs. for a 5 level H atom) Special case of ionization equilibrium: Relaxation time: t = 1 / ( Pk 1 + P 1 k )

T(K) in units of 10 000 K Estimated relaxation times required to achieve the ionization equilibrium from perturbed plasma states (e. g. T and/or p time variations). At high temperatures the relaxation is very fast, at typical CME-core pressures t_relax < 10 sec. Under cool prominence conditions t_relax can reach 1000 sec (also see Engvold 1980, Sol. Phys. 67, 351)