Partial and Total derivatives Derivative of a function

Partial and Total derivatives Derivative of a function of several variables Notation and procedure

Partial and Total derivatives ¢ Last week we saw: l l ¢ That slope of a function f(x) is given by the first derivative of that function f’(x) We also saw the general rule that allows us to find the derivative, as well as some particular rules This week we extend this to the case where the function is a function of several variables l As we saw in previous weeks, in economics we often have functions of several variables

Partial and Total derivatives Partial and total derivatives: concept and notation Rules for carrying out partial and total differentiation

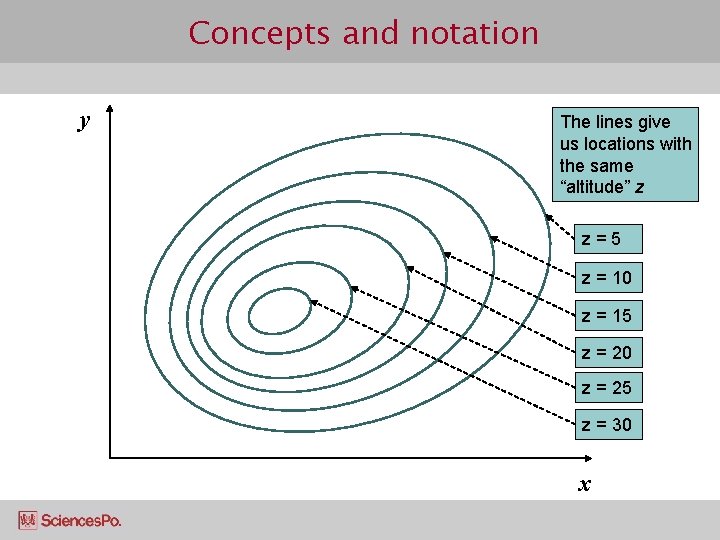
Concepts and notation ¢ ¢ ¢ Imagine that we want to find the slope of a function of x and y Example We know how to do this for a simple function of 1 variable l The concept of total and partial derivatives extends the idea to functions of several variables

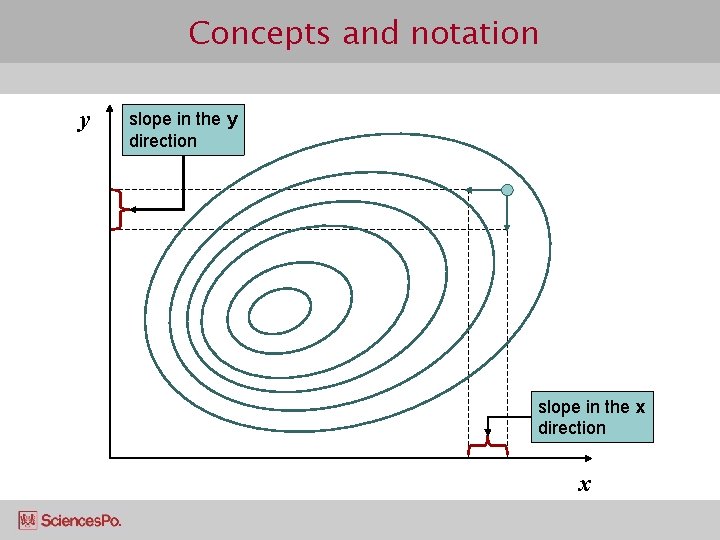
Concepts and notation ¢ The general idea is that we differentiate the function twice, and get slopes in 2 directions l Once as if f were a function of x only l Once as if f were a function of y only l These 2 are the partial derivatives l The sum of the two terms is the total derivative

Concepts and notation y The lines give us locations with the same “altitude” z z=5 z = 10 z = 15 z = 20 z = 25 z = 30 x

Concepts and notation y slope in the y direction slope in the x direction x

Concepts and notation ¢ In order to be able to differentiate the function twice (with respect to x and y), we need to introduce some more notation l l This is so that we don’t get confused when differentiating The notation separates the partials more clearly that the f’ notation

Concepts and notation ¢ In fact, we re-use the notation from last week, but slightly modified: for total derivatives for partial derivatives ¢ Another less used notation is:

Concepts and notation ¢ ¢ For the case of a function of one variable, all these notations are equivalent This is why there was no ‘notation problem’ last week l We didn’t need to separate the different derivatives

Partial and Total derivatives Partial and total derivatives: concept and notation Rules for carrying out partial and total differentiation

Rules of partial/total differentiation ¢ The rules of differentiation do not change from last week l ¢ It is just the order in which things are done, and the meaning of the partial derivative which is different The general rule, with a function of several variables is: l l Calculate the partial derivatives for each of the variable, keeping the other variables constant Add them up to get the total derivative

Rules of partial/total differentiation Example k (constant) 0 f(x) = 3 f’(x)=0 x 1 f(x) = 3 x f’(x)=3 f(x) = 5 x² f’(x)=10 x ¢ These stay the same.

Rules of partial/total differentiation ¢ Let’s practise calculating partial derivatives: y is treated like a constant x is treated like a constant

Rules of partial/total differentiation ¢ Given the partial derivatives, the total derivative is obtained as follows: l The general definition of the total derivative is: l Let’s replace these to get the total derivative

Rules of partial/total differentiation ¢ In economics, we use partial derivatives most of the time l ¢ This means that the main change from last week is just one of notation, and of knowing how to keep the other variables constant Next week we shall see how we can use the set of partial derivatives of a function of several variables to find a maximum/minimum