Part VI NPHardness Lecture 23 Whats NP Hard

Part VI NP-Hardness

Lecture 23 What’s NP?

Hard Problems

Answer What is NP-complete? What is NP-hard? First, what is NP?

Answer 1 NP means “Not Polynomial-time computable”. Wrong! Did you learn automata theory before ?

Answer 2 Still wrong! But, almost true. I can give you a counterexample!

Integer Programming

Decision version of Integer Programming

How to prove a decision problem belonging to NP? How to design a polynomial-time nondeterministic algorithm?

To answer, we need to study computation model, the Turing Machine.

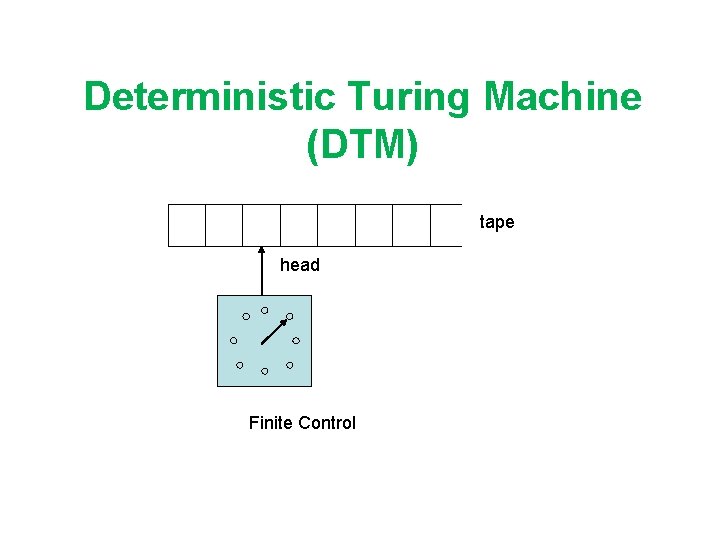
Deterministic Turing Machine (DTM) tape head Finite Control

a l p h a B e The tape has the left end but infinite to the right. It is divided into cells. Each cell contains a symbol in an alphabet Γ. There exists a special symbol B which represents the empty cell.

a • The head scans at a cell on the tape and can read, erase, and write a symbol on the cell. In each move, the head can move to the right cell or to the left cell (or stay in the same cell).

• The finite control has finitely many states which form a set Q. For each move, the state is changed according to the evaluation of a transition function δ : Q x Γ → Q x Γ x {R, L}.

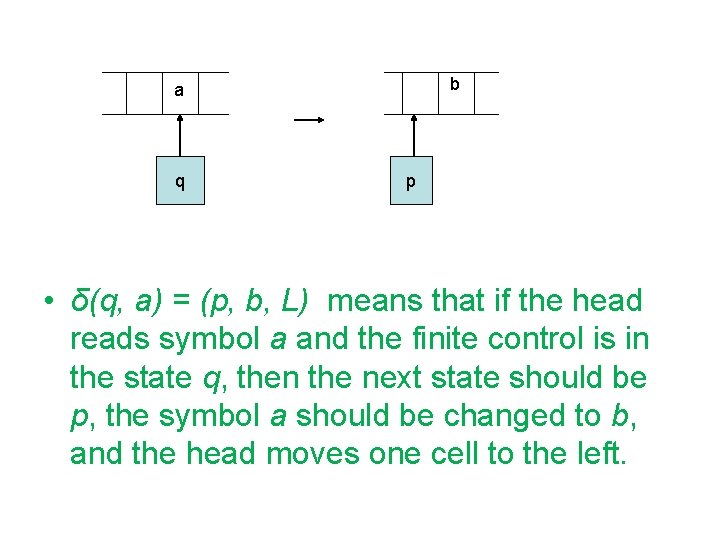
b a q p • δ(q, a) = (p, b, L) means that if the head reads symbol a and the finite control is in the state q, then the next state should be p, the symbol a should be changed to b, and the head moves one cell to the left.

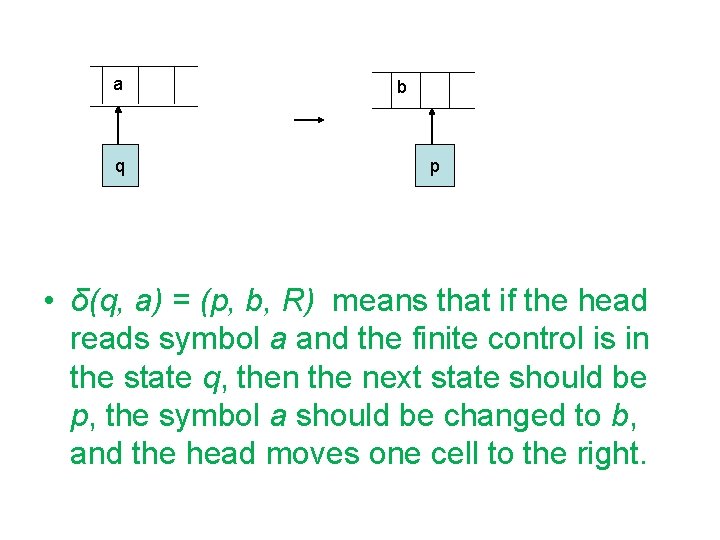
a q b p • δ(q, a) = (p, b, R) means that if the head reads symbol a and the finite control is in the state q, then the next state should be p, the symbol a should be changed to b, and the head moves one cell to the right.

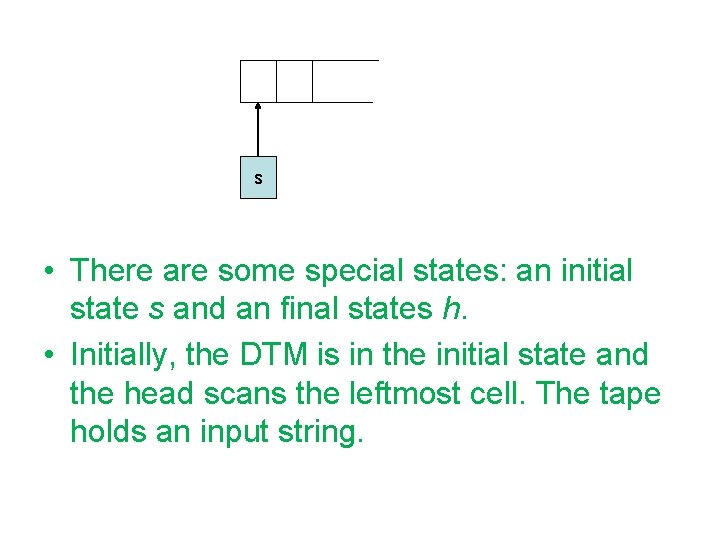
s • There are some special states: an initial state s and an final states h. • Initially, the DTM is in the initial state and the head scans the leftmost cell. The tape holds an input string.

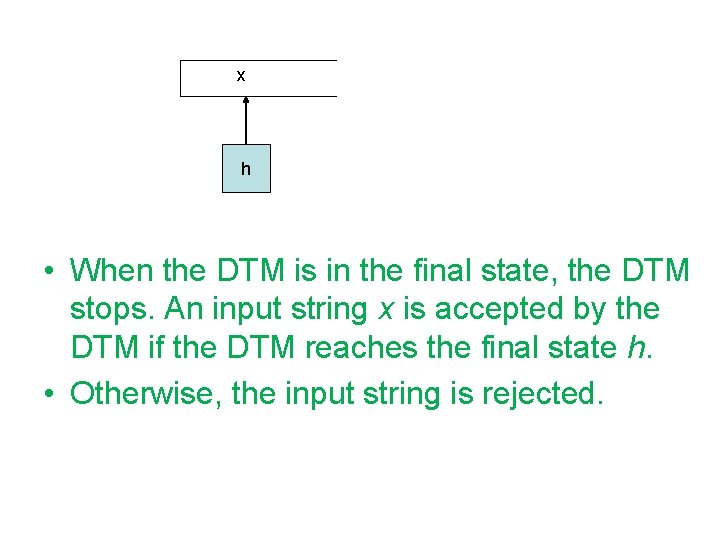
x h • When the DTM is in the final state, the DTM stops. An input string x is accepted by the DTM if the DTM reaches the final state h. • Otherwise, the input string is rejected.

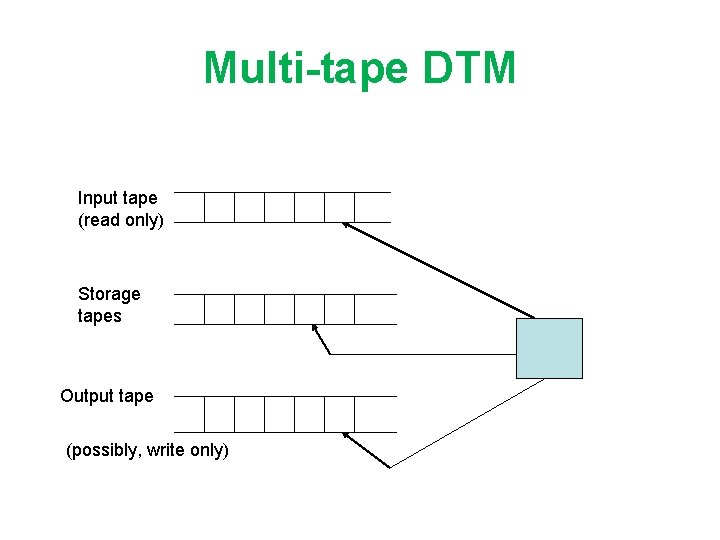
Multi-tape DTM Input tape (read only) Storage tapes Output tape (possibly, write only)

Nondeterministic Turing Machine (NTM) tape head Finite Control

a l p h a B e The tape has the left end but infinite to the right. It is divided into cells. Each cell contains a symbol in an alphabet Γ. There exists a special symbol B which represents the empty cell.

• The finite control has finitely many states which form a set Q. For each move, the state is changed according to the evaluation of a transition function δ : Q x Γ → 2^{Q x Γ x {R, L}}.

Nondeterministic TM (NTM) • There are multiple choices for each transition. • For each input x, the NTM may have more than one computation paths. • An input x is accepted if at least one computation path leads to the final state. • L(M) is the set of all accepted inputs.

Time of DTM • Time. M (x) = # of moves that DTM M takes on input x. • Time. M(x) < infinity iff x ε L(M).

Space • Space. M(x) = maximum # of cells that M visits on each work (storage) tapes during the computation on input x. • If M is a multitape DTM, then the work tapes do not include the input tape and the write-only output tape.

What’s P? • P is a class of decision problems that each can be solved by deterministic TM in polynomial time.

What’s NP? • NP is a class of decision problems that each can be solved by a nondeterministic TM in polynomial time. • NP is a class of decision problems that each can be solved by a polynomial-time nondeterministic algorithm.

What’s PSPACE? • PSPACE is a class of decision problems that each can be solved by TM in polynomial space. • Why didn’t specify Deterministic or Nondeterministic? It doesn’t matter due to Savitch’s Theorem.

P = ? NP = ? PSPACE • They are central problems in computational complexity.

If P = NP, then P NP-complete

Ladner Theorem • If NP ≠ P, then there exists a set A lying between P and NP-complete class, i. e. , A is in NP, but not in P and not being NPcompete.

How to prove a decision problem belonging to NP? How to design a polynomial-time nondeterministic algorithm?

Hamiltonian Cycle • Given a graph G, does G contain a Hamiltonian cycle? • Hamiltonian cycle is a cycle passing every vertex exactly once.

Nondeterministic Algorithm • Guess a permutation of all vertices. • Check whether this permutation gives a cycle. If yes, then algorithm halts. What is the running time?

Guessing Time • Each guess can choose one from a constant number of choices. • This is because that in NTM, the number of choices for each move is independent from input size. • Guessing a permutation of n vertices needs (n long n) time.

Minimum Spanning Tree • Given an edge-weighted graph G, find a spanning tree with minimum total weight. • Decision Version: Given an edge-weighted graph G and a positive integer k, does G contains a spanning tree with total weight < k.

Nondeterministic Algorithm • Guess a spanning tree T. • Check whether the total weight of T < k. This is not clear!

How to guess a spanning tree? • Guess n-1 edges where n is the number of vertices of G. • Check whether those n-1 edges form a connected spanning subgraph, i. e. , there is a path between every pair of vertices.

Co-decision version of MST • Given an edge-weighted graph G and a positive integer k, does G contain no spanning tree with total weight < k?

Algorithm • Computer a minimum spanning tree. • Check whether its weight < k. If yes, the algorithm halts.

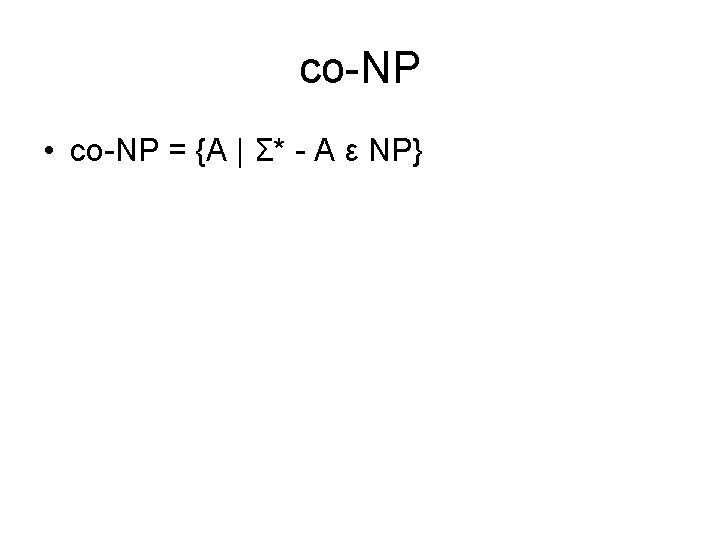
co-NP • co-NP = {A | Σ* - A ε NP}

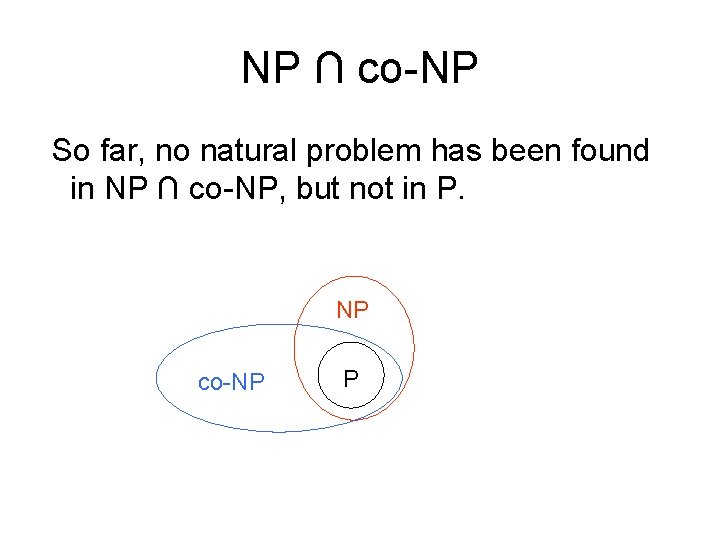
NP ∩ co-NP So far, no natural problem has been found in NP ∩ co-NP, but not in P. NP co-NP P

Linear Programming • Decision version: Given a system of linear inequality, does the system have a solution? • It was first proved in NP ∩ co-NP and later found in P (1979).

Primality Test • Given a natural number n, is n a prime? • It was first proved in NP ∩ co-NP and later found in P (2004).

Therefore • A natural problem belonging to NP ∩ co. NP is a big sign for the problem belonging to P.

Proving a problem in NP • In many cases, it is not hard. • In a few cases, it is not easy.

Polynomial-time verification with polynomial-size certificate

Integer Programming • Decision version: Given A and b, does Ax > b contains an integer solution? • The difficulty is that the domain of “guess” is too large, that is, it is not easy to know the existence of polynomial-size certificate.