Part II Under the Hood How the Graphics

Part II Under the Hood – How the Graphics Pipeline Works

Points and Vectors Lecture 18 Fri, Oct 5, 2007

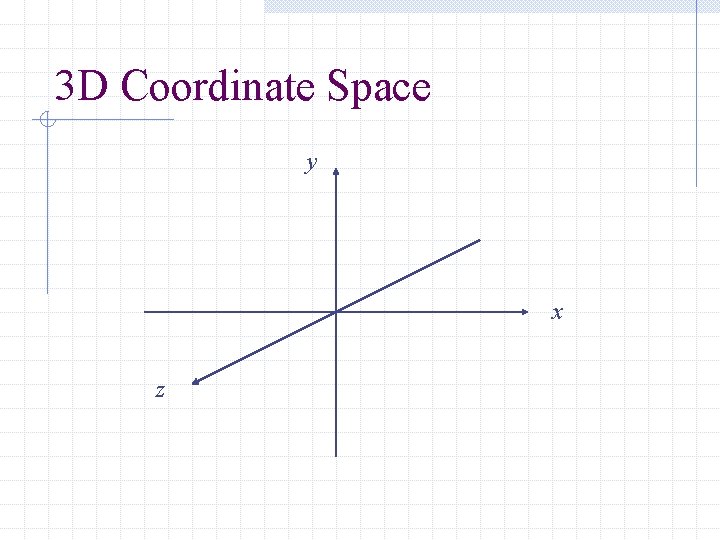
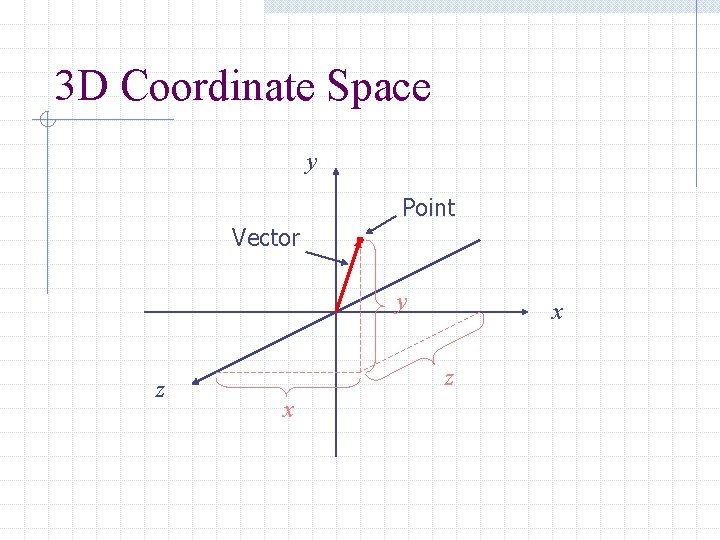
3 D Coordinate Space There are three mutually orthogonal axes: the x-axis, the y-axis, and the z-axis. In the standard viewing position, the x- and y-axes look the same as in the usual 2 D coordinate system. The positive z-axis points towards the viewer; the negative z-axis points away.

3 D Coordinate Space y x z

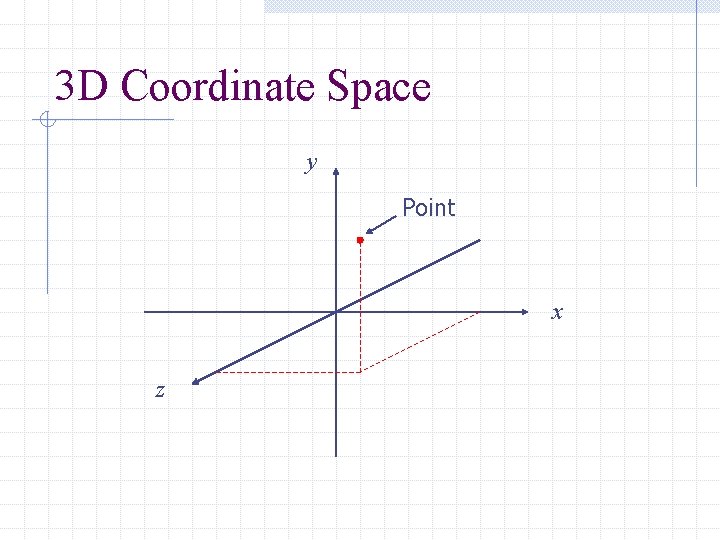
3 D Coordinate Space y Point x z

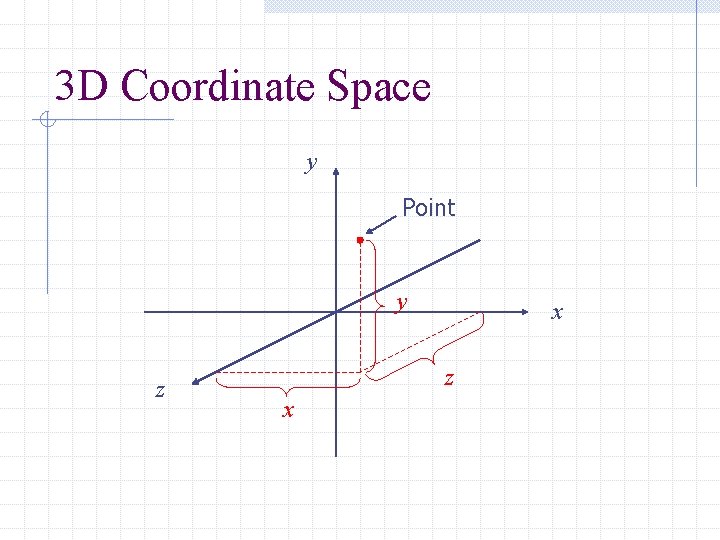
3 D Coordinate Space y Point y z x

Points and Vectors A point specifies a position in space. A vector specifies a direction and a magnitude. Often, our vectors will be normalized to have a length of 1. n In those cases, we will use vectors for direction only.

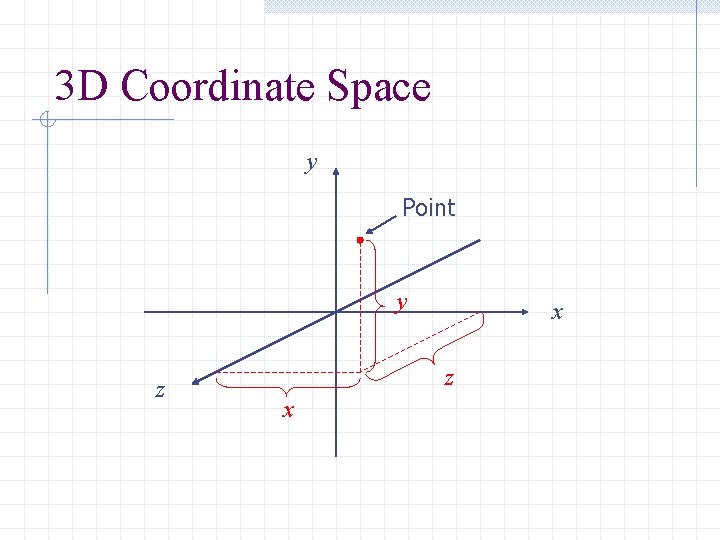
3 D Coordinate Space y Point y z x

3 D Coordinate Space y Point Vector y z x

Homogeneous Coordinates Points and vectors are in homogeneous coordinates (x, y, z, w). n n For points, w 0. For vectors, w = 0. For points, the true 3 -dimensional coordinates are (x/w, y/w, z/w). For this reason, we usually want w = 1.

Points and Vectors Two points determine a vector. B A

Points and Vectors Two points determine a vector. B v=B–A A

Points and Vectors The difference between two points A = (a 1, a 2, a 3, 1) and B = (b 1, b 2, b 3, 1) is the vector B – A = (b 1 – a 1, b 2 – a 2, b 3 – a 3, 0). It is not permissible to add points or to multiply points by a scalar. Why not?

Vector Addition The sum of two vectors is a vector, as defined by the parallogram rule. u v

Vector Addition The sum of two vectors is a vector, as defined by the parallogram rule. u v

Vector Addition The sum of two vectors is a vector, as defined by the parallogram rule. u u+v v

Vector Addition The sum of the vectors u = (u 1, u 2, v 3, 0) and v = (v 1, v 2, v 3, 0) is the vector u + v = (u 1 + v 1, u 2 + v 2, u 3 + v 3, 0).

Vector Subtraction The difference between two vectors is a vector. u v

Vector Subtraction The difference between two vectors is a vector. u–v u v

Vector Subtraction The difference between the vectors u = (u 1, u 2, v 3, 0) and v = (v 1, v 2, v 3, 0) is the vector u – v = (u 1 – v 1, u 2 – v 2, u 3 – v 3, 0).

Scalar Multiplication The product of a vector and a scalar is a vector. v

Scalar Multiplication The product of a vector and a scalar is a vector. 4 v v

Scalar Multiplication The product of a vector and a scalar is a vector. -v v

Scalar Multiplication The product of the vector v = (v 1, v 2, v 3, 0) and the scalar a is the vector av = (av 1, av 2, av 3, 0).

Point-Vector Addition The sum of a point and vector is a point. v A

Point-Vector Addition The sum of a point and vector is a point. B=A+v v A

Point-Vector Addition The sum of the point A = (a 1, a 2, a 3, 1) and the vector v = (v 1, v 2, v 3, 0) is the point A + v = (a 1 + v 1, a 2 + v 2, a 3 + v 3, 1).

Point-Vector Subtraction A point minus a vector is a point. A v

Point-Vector Subtraction The sum of a point and vector is a vector. A -v B=A–v v

Point-Vector Subtraction The difference between the point A = (a 1, a 2, a 3, 1) and the vector v = (v 1, v 2, v 3, 0) is the point A – v = (a 1 – v 1, a 2 – v 2, a 3 – v 3, 1). It is the same as A + (-v).

Point-Vector Arithmetic The following operations should be avoided. n n n Point + point: A + B Scalar * point: a. A Vector – point: v – A Suppose we want to find the midpoint of the line segment from A to B. How could we do it?

Affine Combinations of Points An affine combination of points P 1, P 2, …, Pn, is a linear combination a 1 P 1 + a 2 P 2 + … + an. Pn, where a 1, a 2, …, an are real numbers and a 1 + a 2 + … + an = 1. This is a permissible calculation. What will it produce?

Vector Magnitude The magnitude of a vector is given by the distance formula. Let v = (v 1, v 2, v 3). The magnitude of v, denoted |v|, is given by

Normalized Vectors To normalize a vector, we divide it by its length. That is, for any vector v 0, the unit vector n with the same direction as v is

The Point 3 D and Vector 3 D Classes point 3 d. h, point 3 d. cpp vector 3 d. h, vector 3 d. cpp