Part II Two Variable Statistics Statistical studies often

Part II: Two - Variable Statistics Statistical studies often involve more than one 
variable. We are interested in knowing if there is a 
relationship between the two characteristics for the same 
subject. Example:  A person's age and the time spent using a mobile phone. When the data is quantitative (numbers), the variables be written as an ordered pair (x, y). Correlation is the study and description of the 
 relationship (if any) that exists between the variables. can

A)Qualitative Interpretation of Correlation Data can be organised and displayed in a scatterplot (Cartesian plane) or a contingency table. By inspection, we will describe the type, the direction, and the intensity (or strength) of the relation between the variables.

Type: Refers to the function that best fits the relation  between the variables. We will be using linear  correlation. Direction: If both variables move in the same direction   (increase together or decrease together), then the direction is positive. If both variables move in opposite directions, 
  then direction is negative. Intensity: Strength may be categorised as. . .   Zero, weak, moderate, strong or perfect.

Example: In a gym class students were required to do 
  push-ups and sit-ups. Each student's 
    achievements were recorded as an ordered    pair. The irst number refers to push-ups and 
  the second to sit-ups.     (27, 30), (26, 28), (38, 45), (52, 55), (35, 36), (40, 54), (40, 50), (52, 46), (42, 55), (61, 62), (35, 38), (45, 53), (38, 42), (63, 55), (55, 54), (46, 46), (34, 36), (45, 45), (30, 34), (68, 62)

Contingency Table  A table of values (often involves classes) -Listed down the left side is one variable; listed across 
 he top is the other variable. -Each row and column is added and the totals are 
 isplayed; the bottom right cell shows the total 
 requency of the distribution.

  27, 30), (26, 28), (38, 45), (52, 55), (35, 36),   40, 54), (40, 50), (52, 46), (42, 55), (61, 62),   35, 38), (45, 53), (38, 42), (63, 55), (55, 54),   46, 46), (34, 36), (45, 45), (30, 34), (68, 62)

When the majority of the values fall into a diagonal of 
a contingency table, and the corners contain mostly 
zeros, then the correlation is said to be linear and 
strong. Direction is positive if the diagonal is  Direction is negative if the diagonal is

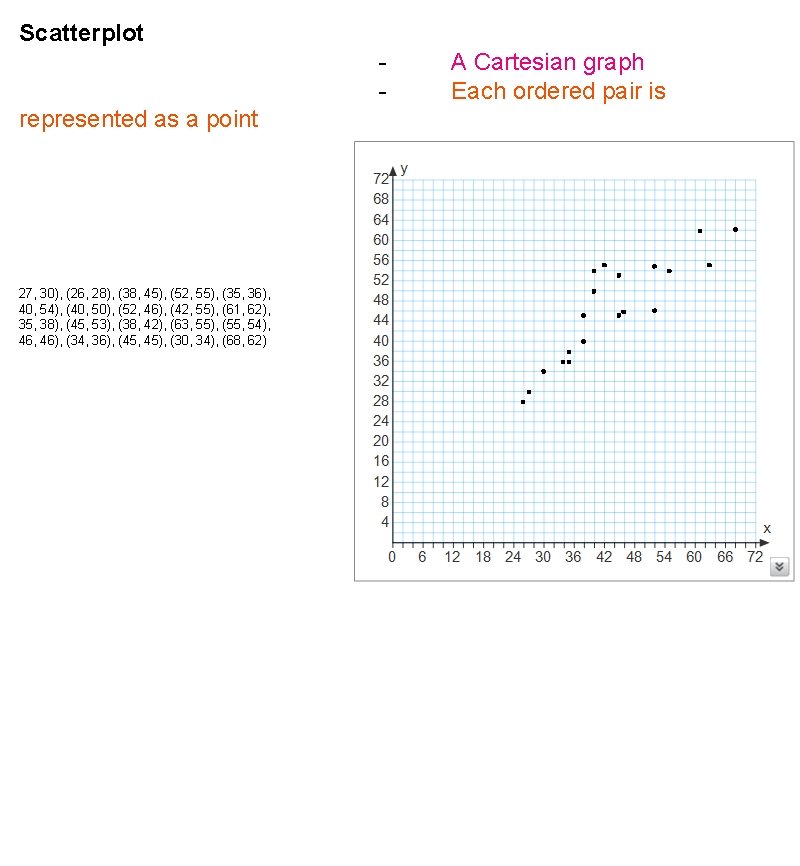
Scatterplot represented as a point   27, 30), (26, 28), (38, 45), (52, 55), (35, 36),   40, 54), (40, 50), (52, 46), (42, 55), (61, 62),   35, 38), (45, 53), (38, 42), (63, 55), (55, 54),   46, 46), (34, 36), (45, 45), (30, 34), (68, 62) A Cartesian graph Each ordered pair is

B)Quantitative Interpretation of Correlation The correlation will be represented by a number, 
 alled the correlation coefficient. This coefficient will range from Its symbol is r. to .

1) raw a scatterplot   27, 30), (26, 28), (38, 45), (52, 55), (35, 36),   40, 54), (40, 50), (52, 46), (42, 55), (61, 62),   35, 38), (45, 53), (38, 42), (63, 55), (55, 54),   46, 46), (34, 36), (45, 45), (30, 34), (68, 62) 2) raw a line that "best fits"  the points. This line passes 
 hrough the middle of the 
 catterplot. Around the points, draw 
 the smallest rectangle 
 possible. Two of the sides should be parallel to the line. 3) 4) easure the dimensions  of the rectangle.

5) alculate the correlation coefficient, r. + f it's increasing,  f it's decreasing ( 2. 4 7. 9 r=+ 1 - ) r = +(1 - 0. 3) r = 0. 7 moderate real r = 0. 87

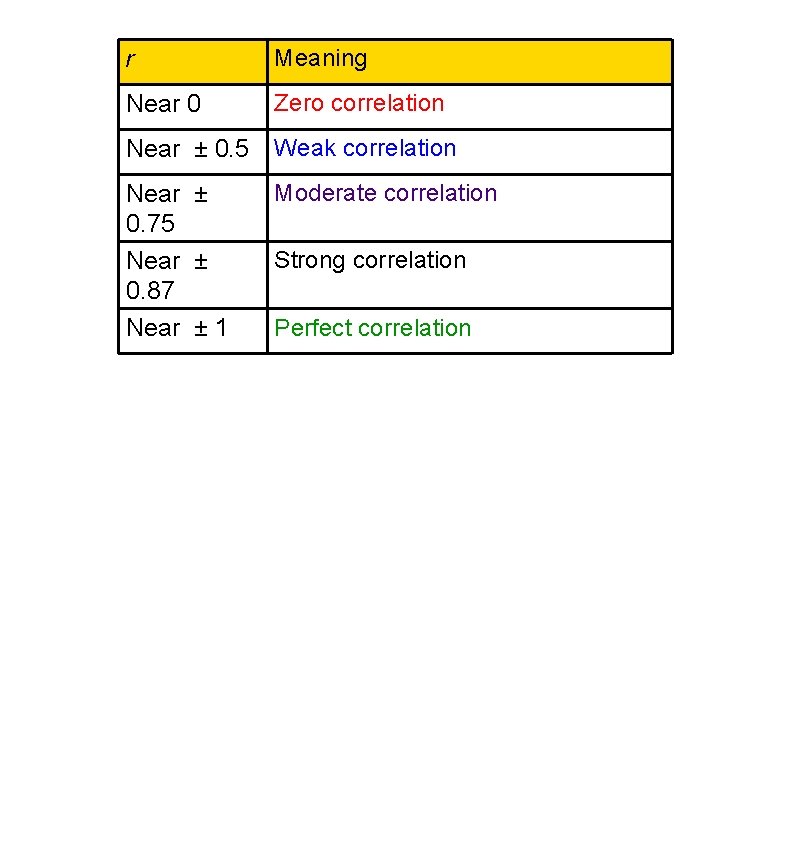
r Meaning Near 0 Zero correlation Near ± 0. 5 Weak correlation Near ± 0. 75 Near ± 0. 87 Near ± 1 Moderate correlation Strong correlation Perfect correlation

The Regression Line Also called a line of best fit, a regression line is one that best represents (or passes through) the points of a scatterplot. It passes through as many points as possible, going through the middle of the scatterplot. There are several different methods of drawing a regression line. The regression line may be used to predict values that 
do not appear in the distribution.

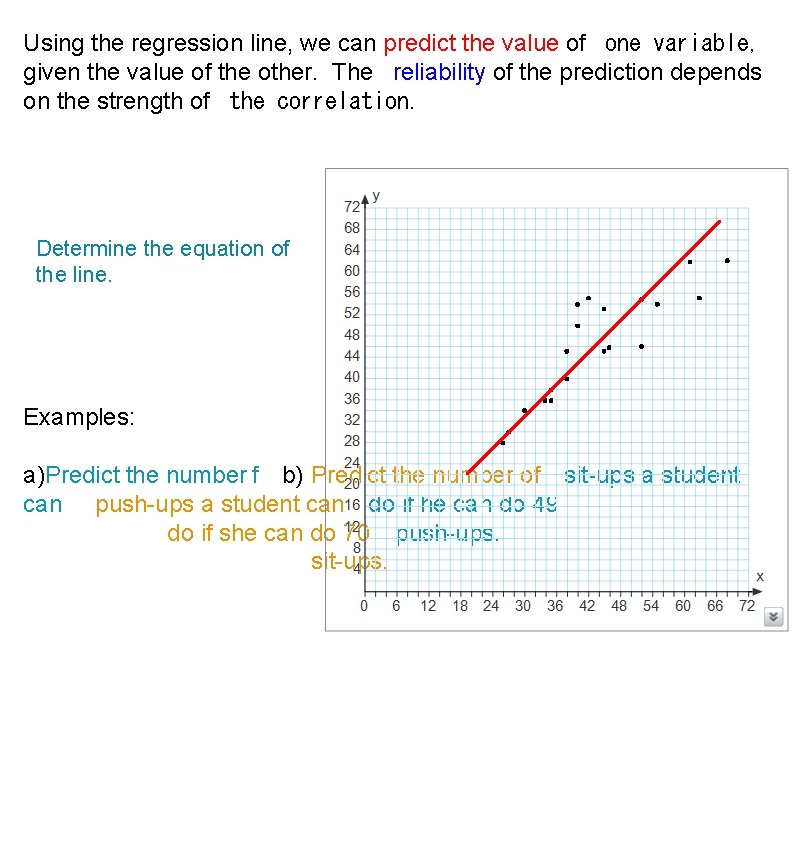
Using the regression line, we can predict the value of 
one variable, given the value of the other. The 
reliability of the prediction depends on the strength of 
the correlation. Determine the equation of the line. Examples: a)Predict the number f   b) Predict the number of 
 sit-ups a student can    push-ups a student can 
 do if he can do 49   do if she can do 70 
push-ups.   sit-ups.

Recall: predicted actual Since the correlation is moderate/high, we can be confident that our predictions are good.

Interpreting a Correlation A strong correlation indicates that there is a 
 tatistical relationship between two variables.  t does not, however, explain the reason for the 
 elationship or its nature.  here are other things to consider. . .

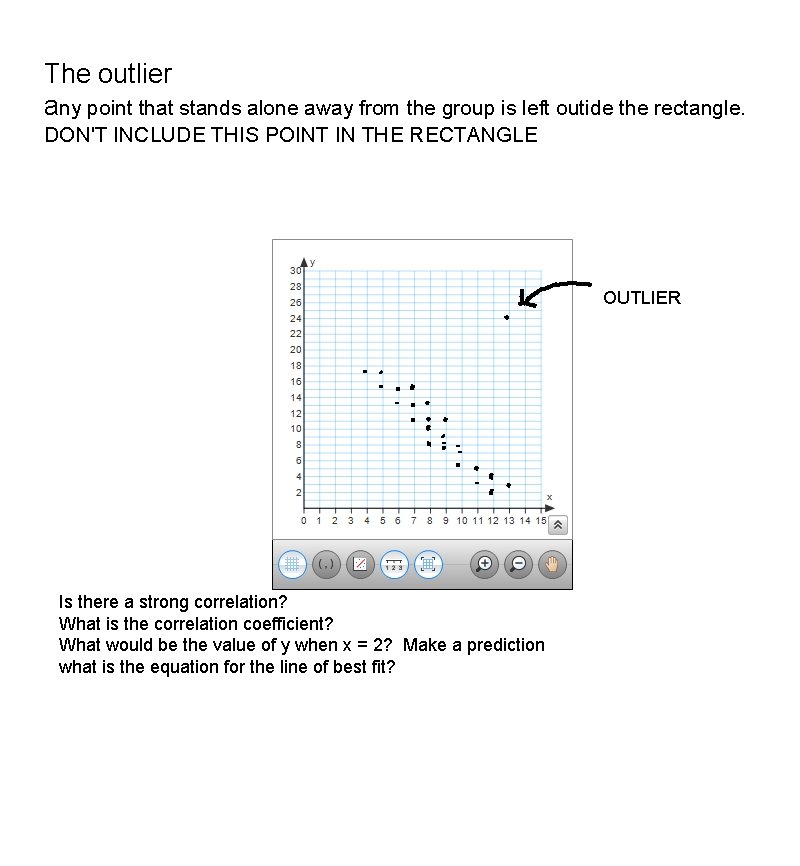
The outlier any point that stands alone away from the group is left outide the rectangle. DON'T INCLUDE THIS POINT IN THE RECTANGLE OUTLIER Is there a strong correlation? What is the correlation coefficient? What would be the value of y when x = 2? Make a prediction what is the equation for the line of best fit?