Part II Concepts 1 The structure of a

Part II Concepts 1

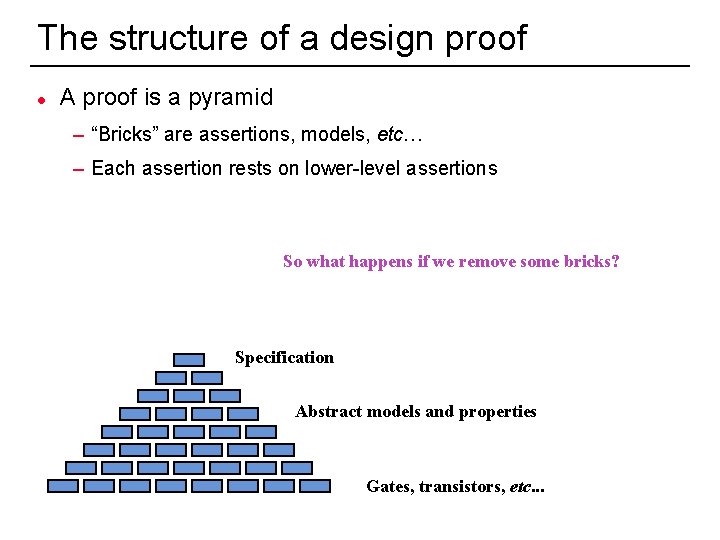
The structure of a design proof l A proof is a pyramid – “Bricks” are assertions, models, etc… – Each assertion rests on lower-level assertions So what happens if we remove some bricks? Specification Abstract models and properties Gates, transistors, etc. . . 2

Local property verification l Verify properties of small parts of design, e. g… – Bus protocol conformance – No pipeline hazards l Like type checking, rules out certain localized errors Although this leaves a rather large gap. . . Specification GAP Properties verified (or RTL equivalence) Gates, transistors, etc. . . 3

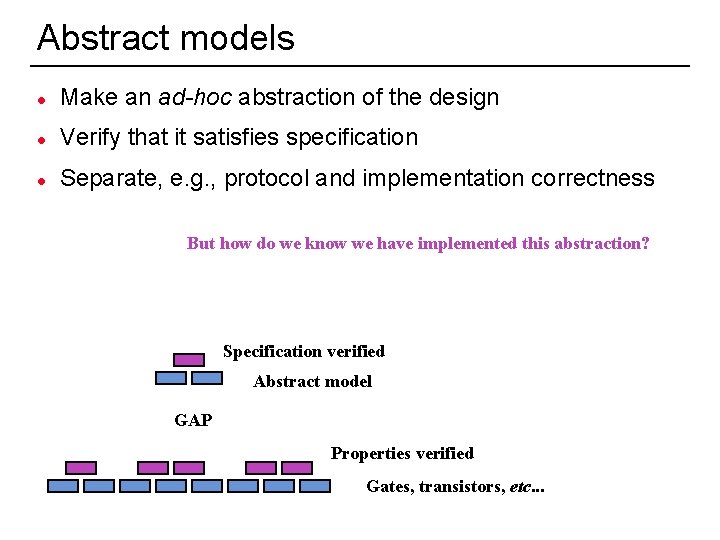
Abstract models l Make an ad-hoc abstraction of the design l Verify that it satisfies specification l Separate, e. g. , protocol and implementation correctness But how do we know we have implemented this abstraction? Specification verified Abstract model GAP Properties verified Gates, transistors, etc. . . 4

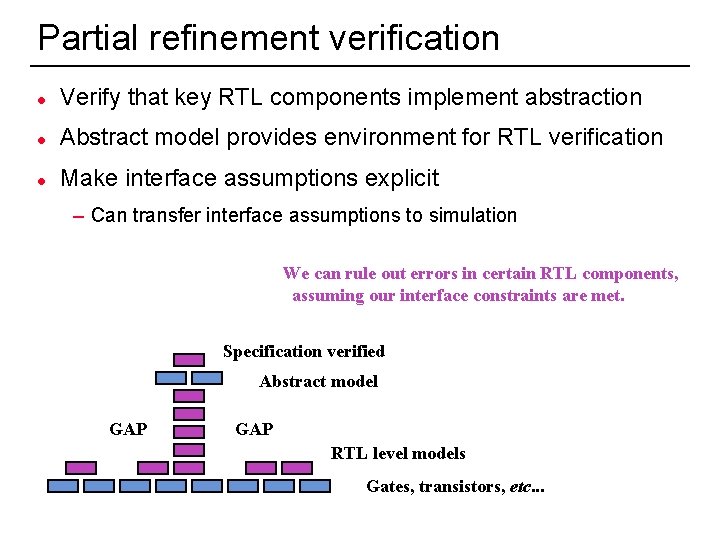
Partial refinement verification l Verify that key RTL components implement abstraction l Abstract model provides environment for RTL verification l Make interface assumptions explicit – Can transfer interface assumptions to simulation We can rule out errors in certain RTL components, assuming our interface constraints are met. Specification verified Abstract model GAP RTL level models Gates, transistors, etc. . . 5

Overview l Property specification and verification – temporal logic model checking – finite automata and language containment – symbolic trajectory evaluation l Abstraction – system-level finite-state abstractions – abstraction with uninterpreted function symbols l Refinement verification – refinement maps – cache coherence example 6

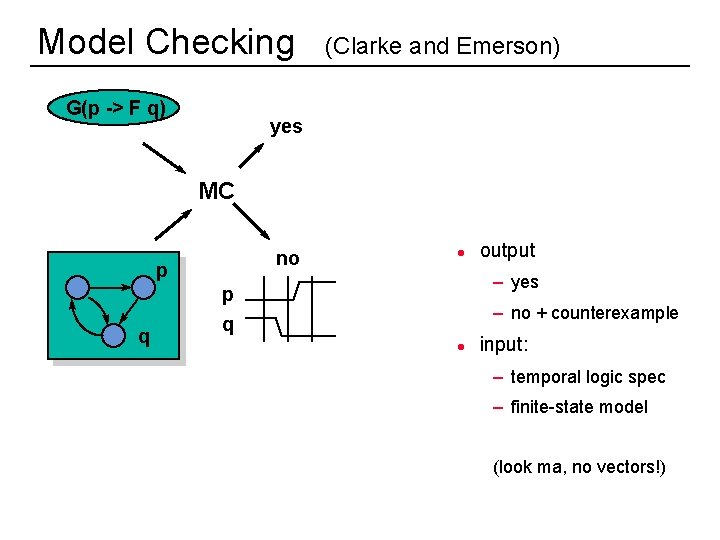
Model Checking G(p -> F q) (Clarke and Emerson) yes MC no p q l output – yes p q – no + counterexample l input: – temporal logic spec – finite-state model (look ma, no vectors!) 7

Linear temporal logic (LTL) l A logical notation that allows to: – specify relations in time – conveniently express finite control properties l 8 Temporal operators –Gp “henceforth p” –Fp “eventually p” –Xp “p at the next time” –p. Wq “p unless q”

Types of temporal properties l Safety (nothing bad happens) G ~(ack 1 & ack 2) “mutual exclusion” G (req -> (req W ack)) ack” l Liveness G (req -> F ack) l (something good happens) “if req, eventually ack” Fairness GF req -> GF ack 9 “req must hold until “if infinitely often req, infinitely often ack”

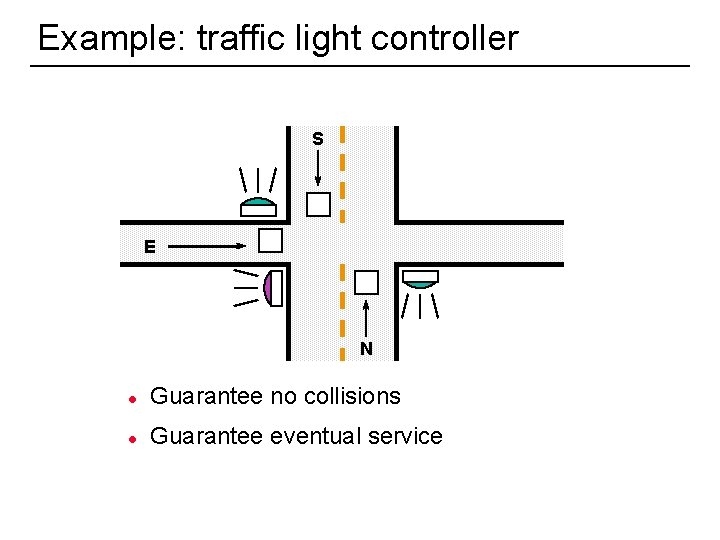
Example: traffic light controller S E N 10 l Guarantee no collisions l Guarantee eventual service

Controller program module main(N_SENSE, S_SENSE, E_SENSE, N_GO, S_GO, E_GO); input N_SENSE, S_SENSE, E_SENSE; output N_GO, S_GO, E_GO; reg NS_LOCK, EW_LOCK, N_REQ, S_REQ, E_REQ; /* set request bits when sense is high */ always begin if (!N_REQ & N_SENSE) N_REQ = 1; end always begin if (!S_REQ & S_SENSE) S_REQ = 1; end always begin if (!E_REQ & E_SENSE) E_REQ = 1; end 11

Example continued. . . /* controller for North light */ always begin if (N_REQ) begin wait (!EW_LOCK); NS_LOCK = 1; N_GO = 1; wait (!N_SENSE); if (!S_GO) NS_LOCK = 0; N_GO = 0; N_REQ = 0; end /* South light is similar. . . */ 12

Example code, cont… /* Controller for East light */ always begin if (E_REQ) begin EW_LOCK = 1; wait (!NS_LOCK); E_GO = 1; wait (!E_SENSE); EW_LOCK = 0; E_GO = 0; E_REQ = 0; end 13

Specifications in temporal logic l Safety (no collisions) G ~(E_Go & (N_Go | S_Go)); l Liveness G (~N_Go & N_Sense -> F N_Go); G (~S_Go & S_Sense -> F S_Go); G (~E_Go & E_Sense -> F E_Go); l Fairness constraints GF ~(N_Go & N_Sense); GF ~(S_Go & S_Sense); GF ~(E_Go & E_Sense); /* assume each sensor off infinitely often */ 14

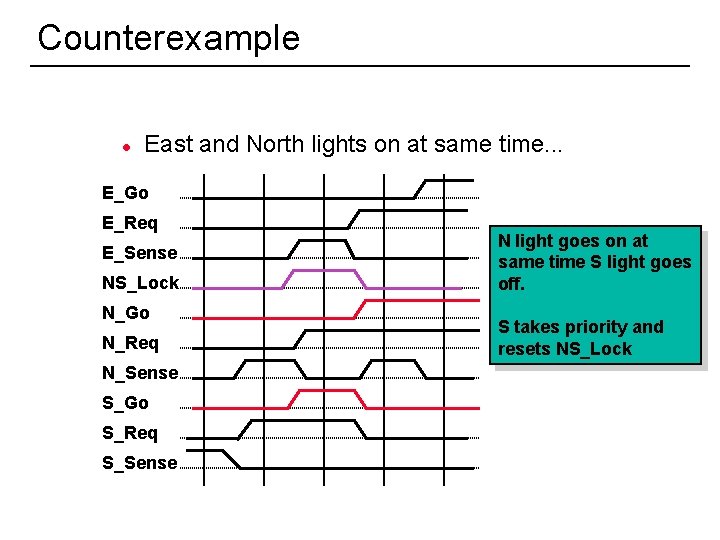
Counterexample l East and North lights on at same time. . . E_Go E_Req E_Sense NS_Lock N_Go N_Req N_Sense S_Go S_Req S_Sense 15 N light goes on at same time S light goes off. S takes priority and resets NS_Lock

Fixing the error l Don’t allow N light to go on while south light is going off. always begin if (N_REQ) begin wait (!EW_LOCK & !(S_GO & !S_SENSE)); NS_LOCK = 1; N_GO = 1; wait (!N_SENSE); if (!S_GO) NS_LOCK = 0; N_GO = 0; N_REQ = 0; end 16

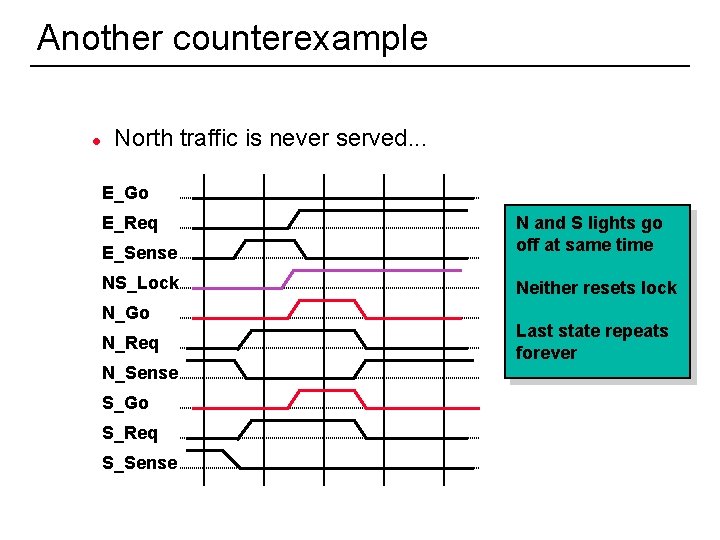
Another counterexample l North traffic is never served. . . E_Go E_Sense N and S lights go off at same time NS_Lock Neither resets lock E_Req N_Go N_Req N_Sense S_Go S_Req S_Sense 17 Last state repeats forever

Fixing the liveness error l When N light goes off, test whether S light is also going off, and if so reset lock. always begin if (N_REQ) begin wait (!EW_LOCK & !(S_GO & !S_SENSE)); NS_LOCK = 1; N_GO = 1; wait (!N_SENSE); if (!S_GO | !S_SENSE) NS_LOCK = 0; N_GO = 0; N_REQ = 0; end 18

All properties verified l Guarantee no collisions l Guarantee service assuming fairness l Computational resources used: – 57 states searched – 0. 1 CPU seconds 19

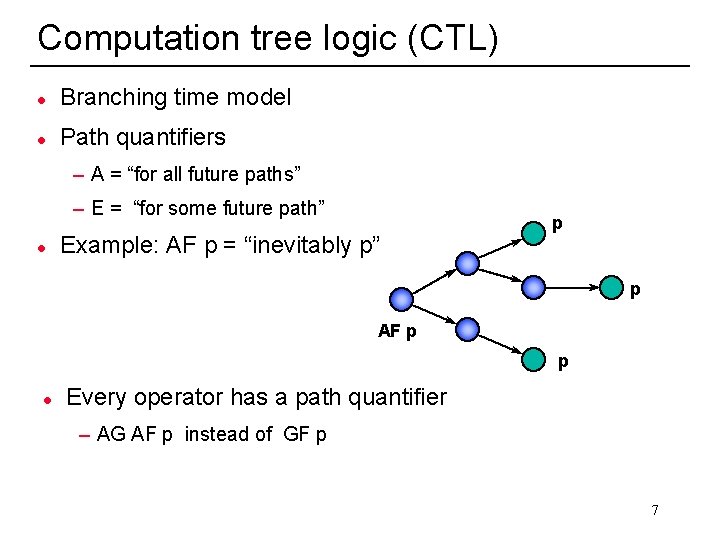
Computation tree logic (CTL) l Branching time model l Path quantifiers – A = “for all future paths” – E = “for some future path” l Example: AF p = “inevitably p” p p AF p p l Every operator has a path quantifier – AG AF p instead of GF p 20 7

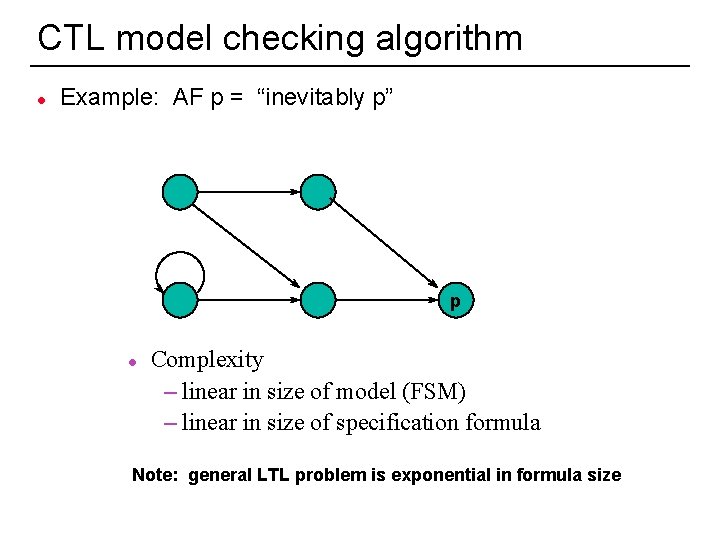
Difference between CTL and LTL l Think of CTL formulas as approximations to LTL – AG EF p is weaker than G F p Good for finding bugs. . . p – AF AG p is stronger than F G p p l p Good for verifying. . . CTL formulas easier to verify So, use CTL when it applies. . . 21 8

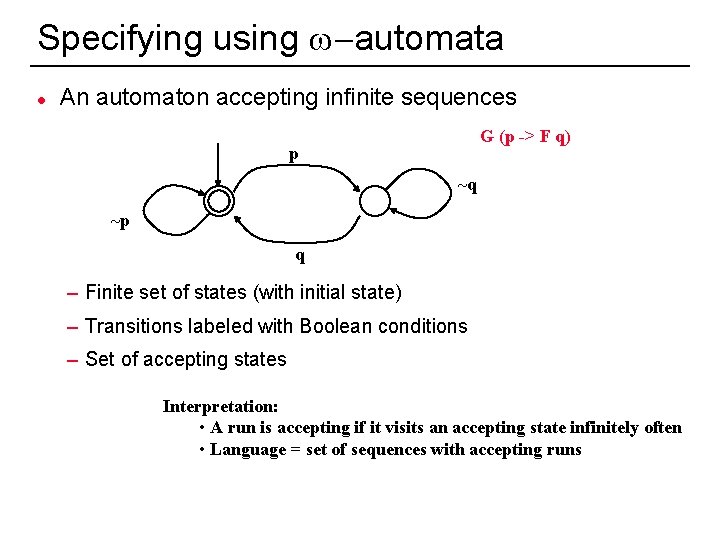
CTL model checking algorithm l Example: AF p = “inevitably p” p l Complexity – linear in size of model (FSM) – linear in size of specification formula Note: general LTL problem is exponential in formula size 22

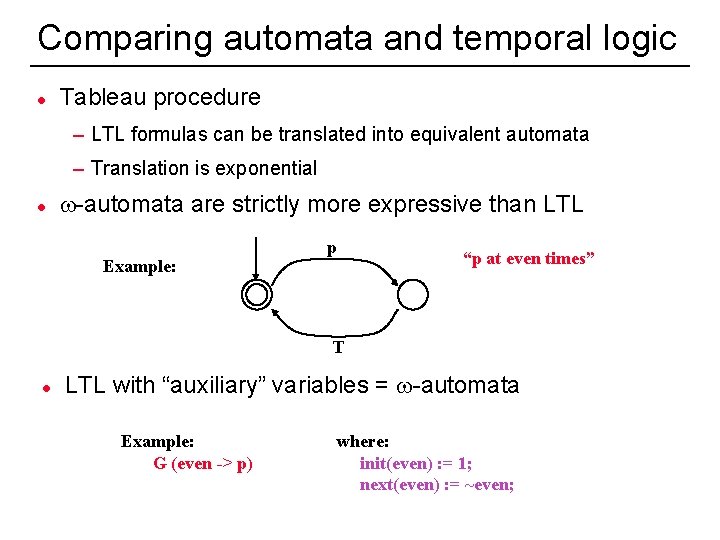
Specifying using w-automata l An automaton accepting infinite sequences G (p -> F q) p ~q ~p q – Finite set of states (with initial state) – Transitions labeled with Boolean conditions – Set of accepting states Interpretation: • A run is accepting if it visits an accepting state infinitely often • Language = set of sequences with accepting runs 23

Verifying using w-automata l Construct parallel product of model and automaton l Search for “bad cycles” – Very similar algorithm to temporal logic model checking l Complexity (deterministic automaton) – Linear in model size – Linear in number of automaton states – Complexity in number of acceptance conditions varies 24

Comparing automata and temporal logic l Tableau procedure – LTL formulas can be translated into equivalent automata – Translation is exponential l w-automata are strictly more expressive than LTL Example: p “p at even times” T l LTL with “auxiliary” variables = w-automata Example: G (even -> p) 25 where: init(even) : = 1; next(even) : = ~even;

State explosion problem l What if the state space is too large? – too much parallelism – data in model l Approaches – “Symbolic” methods (BDD’s) – Abstraction/refinement – Exploit symmetry – Exploit independence of actions 26

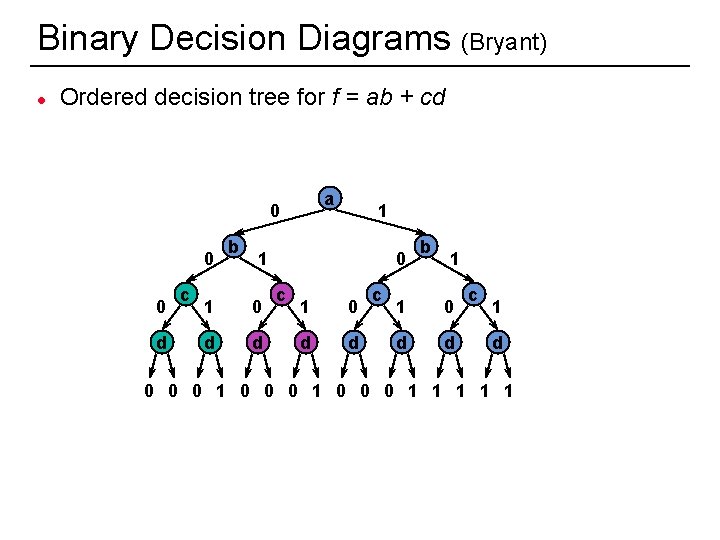
Binary Decision Diagrams (Bryant) l Ordered decision tree for f = ab + cd a 0 0 0 d c b 1 1 1 0 d d 0 c 1 0 d d c b 1 1 0 d d c 1 d 0 0 0 1 1 1 27

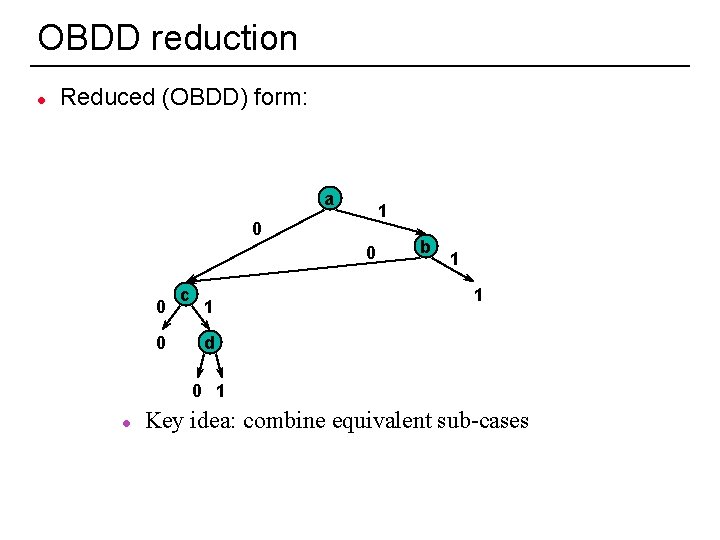
OBDD reduction l Reduced (OBDD) form: a 1 0 0 c 1 b 1 1 d 0 1 l 28 Key idea: combine equivalent sub-cases

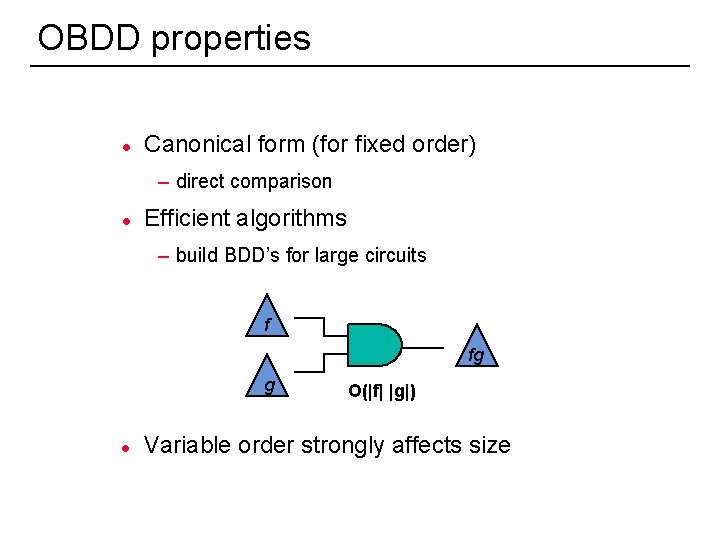
OBDD properties l Canonical form (for fixed order) – direct comparison l Efficient algorithms – build BDD’s for large circuits f fg g l 29 O(|f| |g|) Variable order strongly affects size

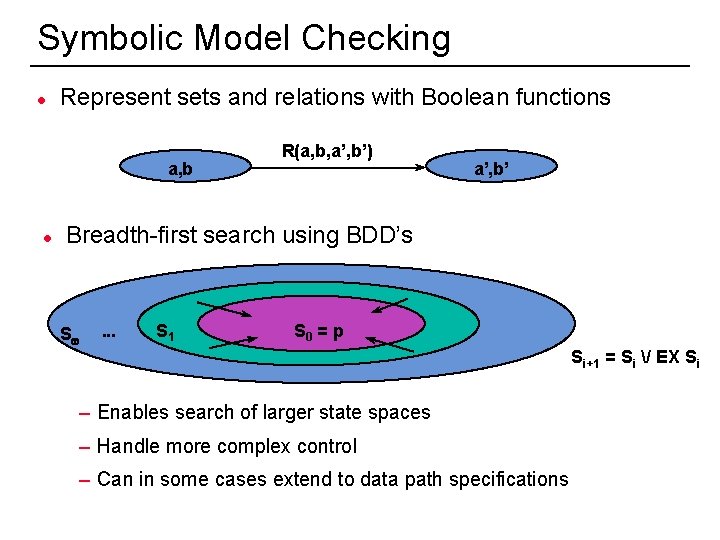
Symbolic Model Checking l Represent sets and relations with Boolean functions a, b l R(a, b, a’, b’) a’, b’ Breadth-first search using BDD’s Sw . . . S 1 S 0 = p – Enables search of larger state spaces – Handle more complex control – Can in some cases extend to data path specifications 30 Si+1 = Si / EX Si

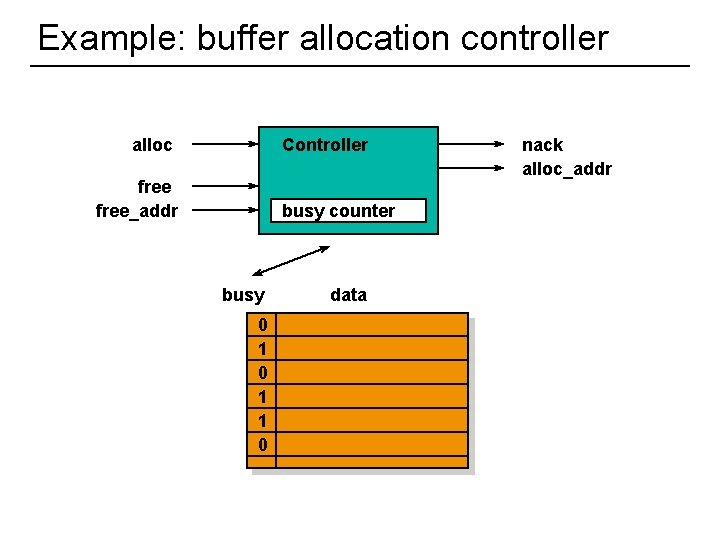
Example: buffer allocation controller alloc Controller free_addr busy counter busy 0 1 1 0 31 data nack alloc_addr

Verilog description assign nack = alloc & (count == `SIZE); assign count = count + (alloc & ~nack) - free; always begin if(free) busy[free_addr] = 0; if(alloc & ~nack) busy[alloc_addr] = 1; end always begin for(i = (`SIZE - 1); i >= 0; i = i - 1) if (~busy[i]) alloc_addr = i; end 32

LTL specifications l Alloc’d buffer may not be realloc’d until freed allocd[i] = alloc & ~nack & alloc_addr = i; freed[i] = free & free_addr = i; G (allocd[i] -> (~allocd[i] W freed[i]); l Must assume the following always holds: – G (free -> busy[free_addr]); 33

Verification results SIZE = 32 buffers: Time 68 s BDD nodes used transition relation reached state set total Total number of states 34 ~7000 ~60000 4 G

Why are BDD’s effective? l Combining equivalent subcases: busy[0] All cases where sum of busy = x are equivalent 0 1 0 1 0 1 busy[1] busy[2] 0 1 count[0] 0 1 0 0 1 1 count[1] 1 35 1 1 1

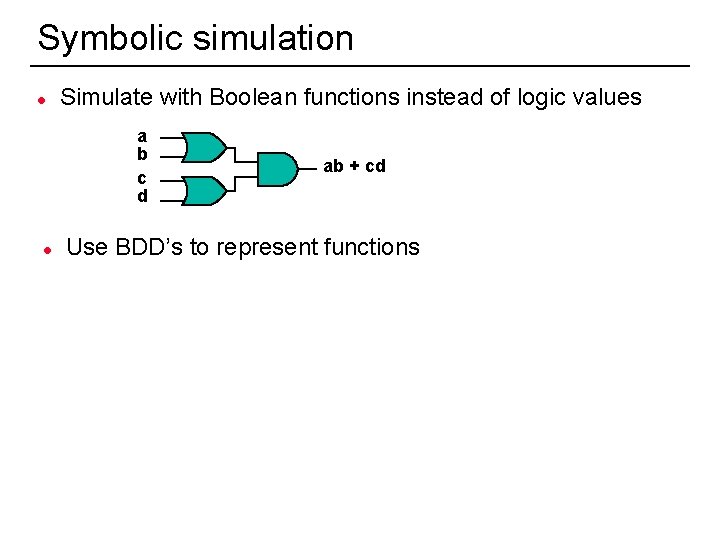
Symbolic simulation l Simulate with Boolean functions instead of logic values a b c d l 36 ab + cd Use BDD’s to represent functions

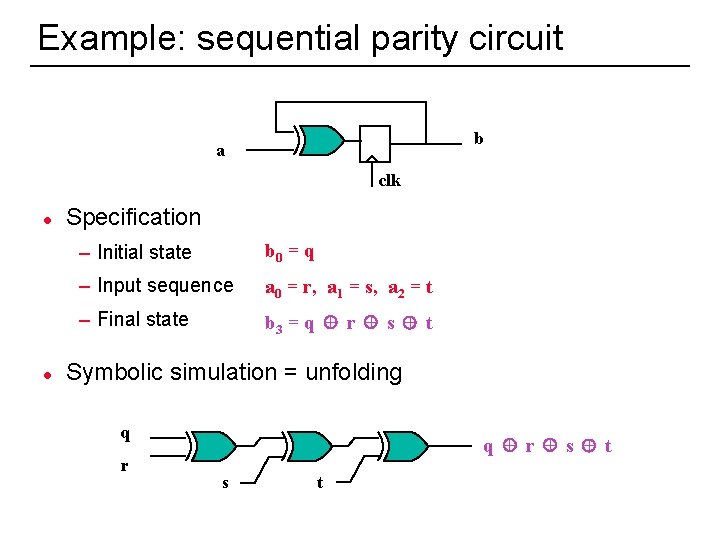
Example: sequential parity circuit b a clk l l Specification – Initial state b 0 = q – Input sequence a 0 = r, a 1 = s, a 2 = t – Final state b 3 = q + r + s + t Symbolic simulation = unfolding q r 37 q + r + s + t s t

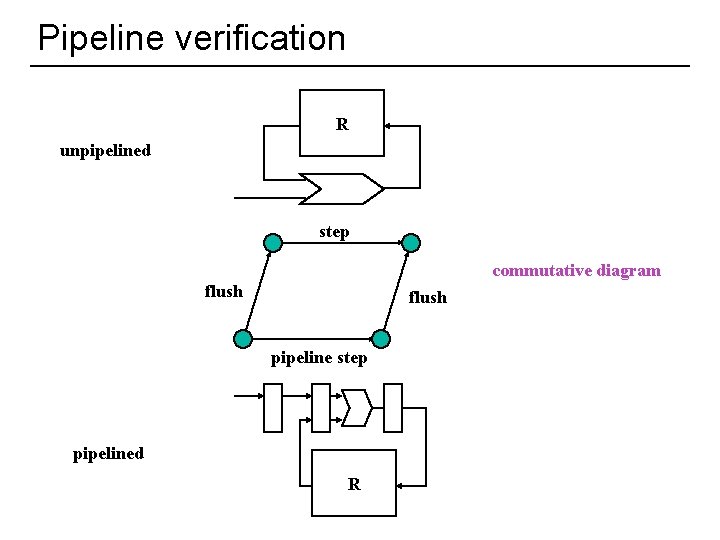
Pipeline verification R unpipelined step commutative diagram flush pipeline step pipelined R 38

Property verification Specification GAP Properties verified (or RTL equivalence) Gates, transistors, etc. . . l Like type checking… – Rules out certain localized errors – Static -- requires no vectors l 39 Does not guarantee correct interaction of components

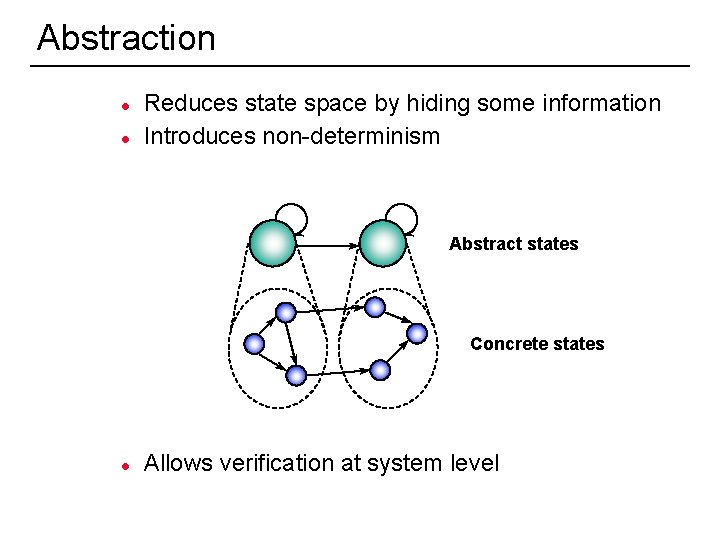
Abstraction l l Reduces state space by hiding some information Introduces non-determinism Abstract states Concrete states l 40 Allows verification at system level

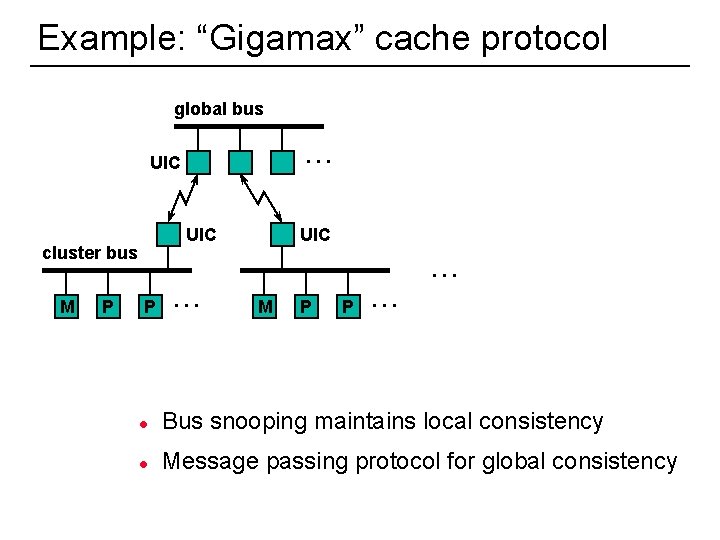
Example: “Gigamax” cache protocol global bus. . . UIC cluster bus M 41 P UIC. . . P . . . M P P . . . l Bus snooping maintains local consistency l Message passing protocol for global consistency

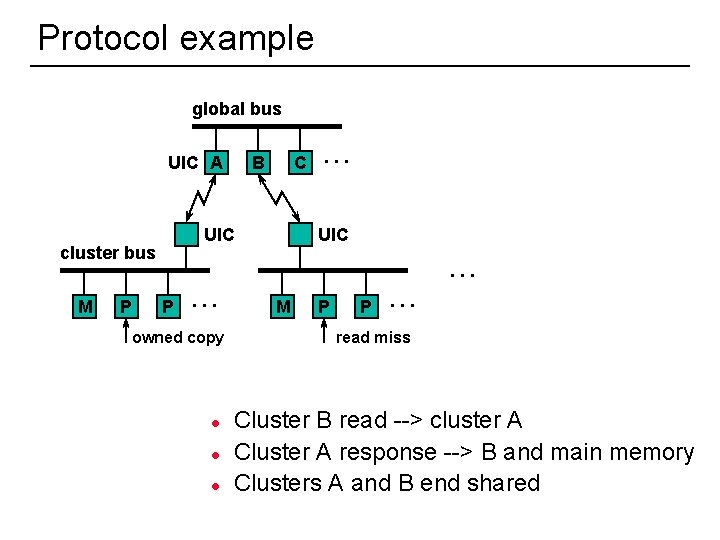
Protocol example global bus UIC A UIC cluster bus M P UIC. . . P . . . owned copy l l l 42 C. . . B M P P . . . read miss Cluster B read --> cluster A Cluster A response --> B and main memory Clusters A and B end shared

Protocol correctness issues l Protocol issues – deadlock – unexpected messages – liveness l Coherence – each address is sequentially consistent – store ordering (system dependent) l 43 Abstraction is relative to properties specified

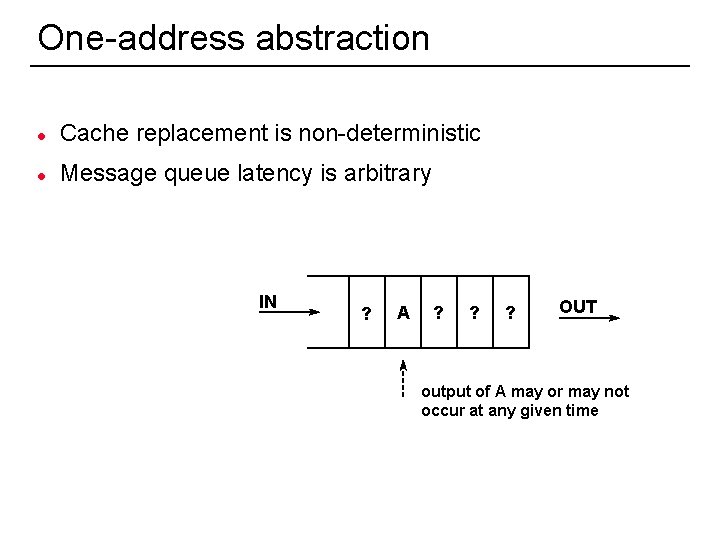
One-address abstraction l Cache replacement is non-deterministic l Message queue latency is arbitrary IN ? A ? ? ? OUT output of A may or may not occur at any given time 44

Specifications l Absence of deadlock SPEC AG (EF p. readable & EF p. writable); l Coherence SPEC AG((p. readable & bit -> ~EF(p. readable & ~bit)); Abstraction: bit = 45 { 0 1 if data < n otherwise

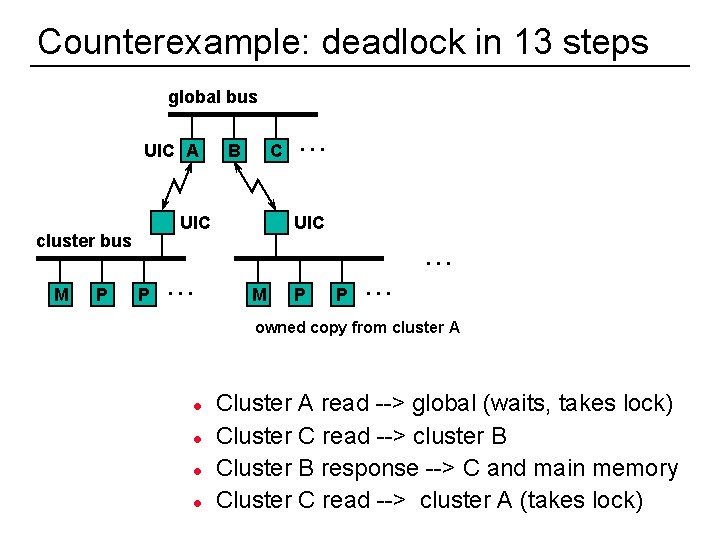
Counterexample: deadlock in 13 steps global bus UIC A UIC cluster bus M P C. . . B UIC. . . P . . . M P P . . . owned copy from cluster A l l 46 Cluster A read --> global (waits, takes lock) Cluster C read --> cluster B Cluster B response --> C and main memory Cluster C read --> cluster A (takes lock)

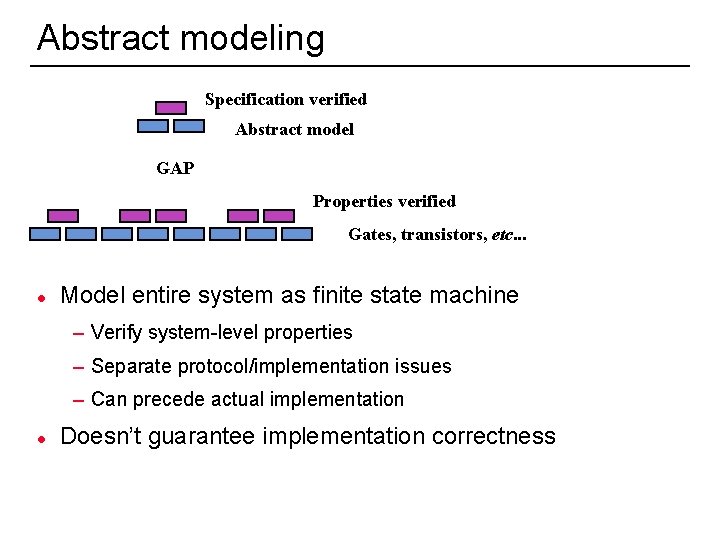
Abstract modeling Specification verified Abstract model GAP Properties verified Gates, transistors, etc. . . l Model entire system as finite state machine – Verify system-level properties – Separate protocol/implementation issues – Can precede actual implementation l 47 Doesn’t guarantee implementation correctness

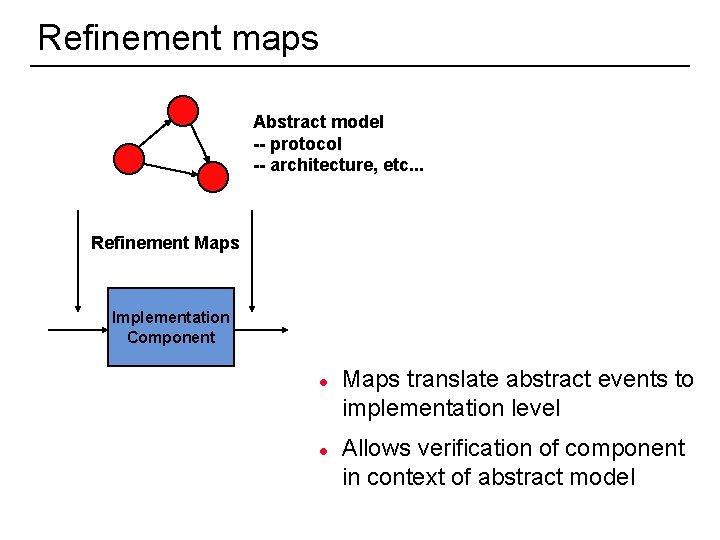
Refinement maps Abstract model -- protocol -- architecture, etc. . . Refinement Maps Implementation Component l l 48 Maps translate abstract events to implementation level Allows verification of component in context of abstract model

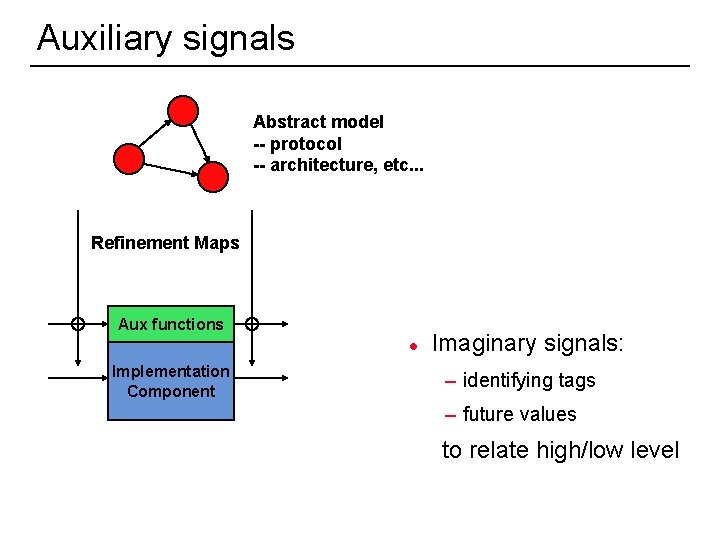
Auxiliary signals Abstract model -- protocol -- architecture, etc. . . Refinement Maps Aux functions l Implementation Component Imaginary signals: – identifying tags – future values to relate high/low level 49

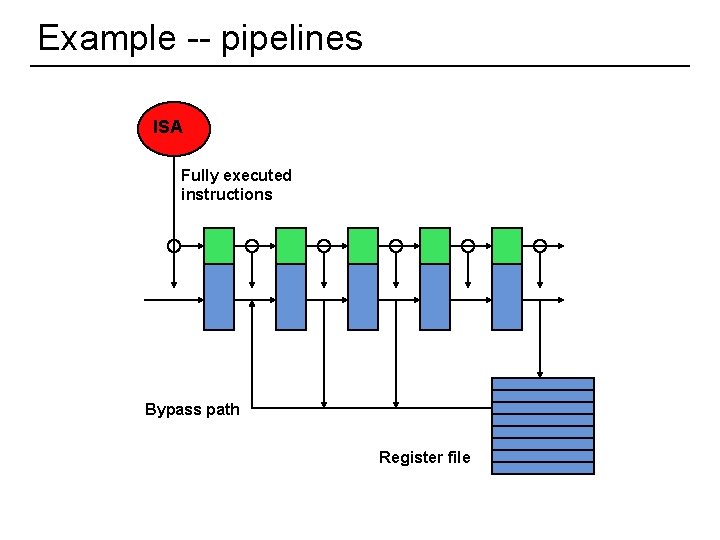
Example -- pipelines ISA Fully executed instructions Bypass path Register file 50

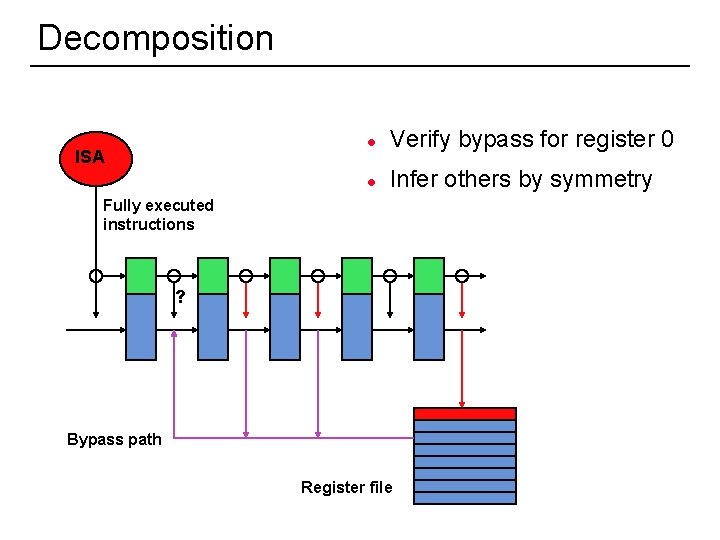
Decomposition ISA l Verify bypass for register 0 l Infer others by symmetry Fully executed instructions ? Bypass path Register file 51

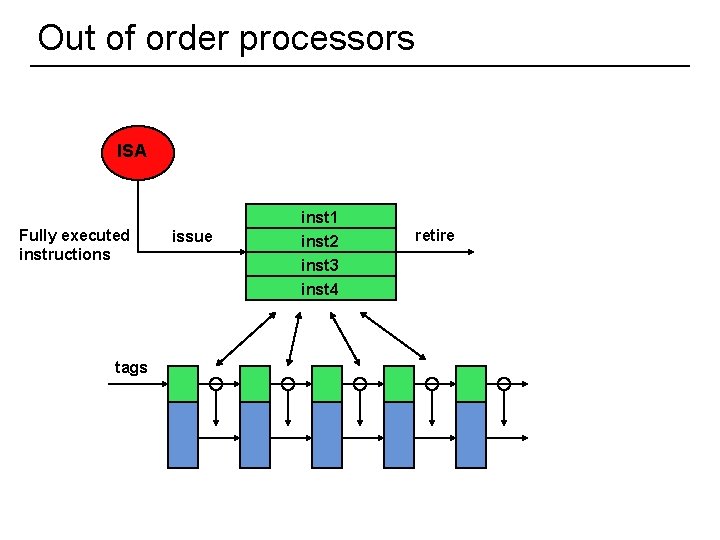
Out of order processors ISA Fully executed instructions tags 52 issue inst 1 inst 2 inst 3 inst 4 retire

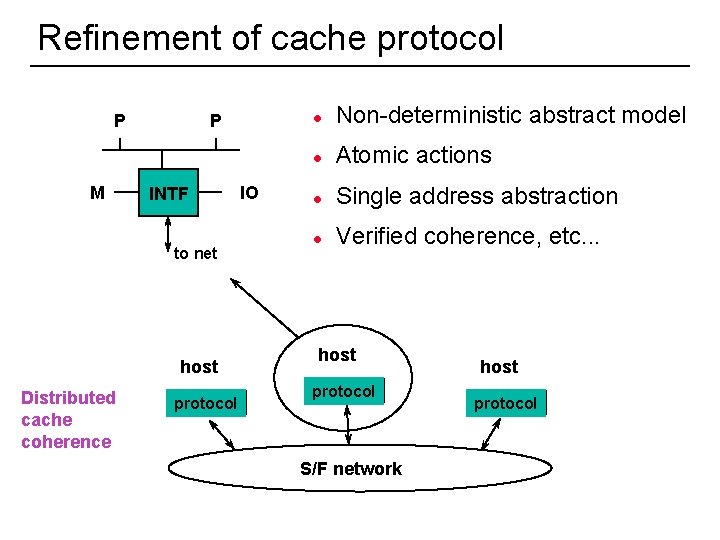
Refinement of cache protocol P M P INTF to net host Distributed cache coherence protocol IO l Non-deterministic abstract model l Atomic actions l Single address abstraction l Verified coherence, etc. . . host protocol S/F network 53 host protocol

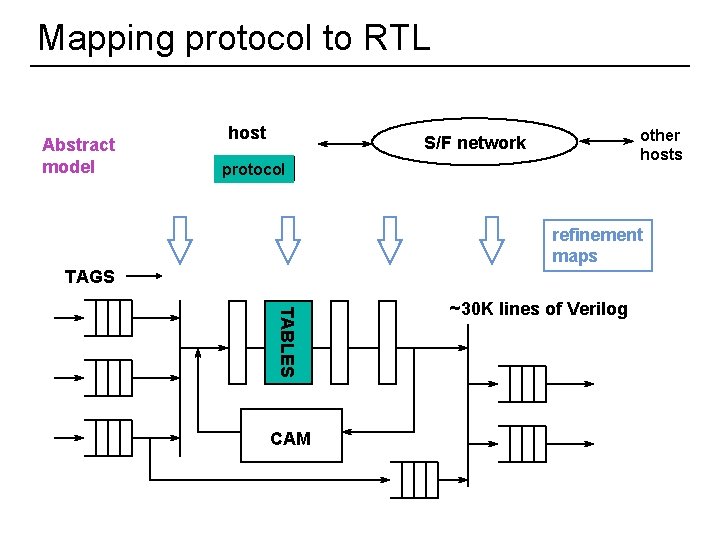
Mapping protocol to RTL Abstract model host other hosts S/F network protocol refinement maps TAGS TABLES CAM 54 ~30 K lines of Verilog

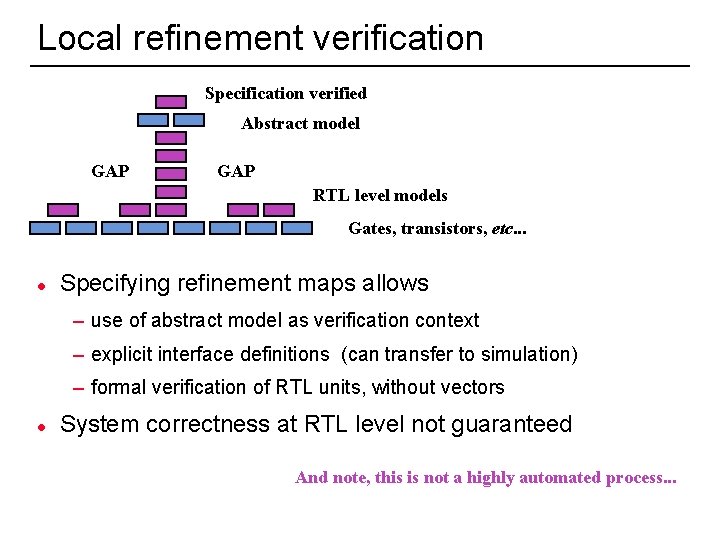
Local refinement verification Specification verified Abstract model GAP RTL level models Gates, transistors, etc. . . l Specifying refinement maps allows – use of abstract model as verification context – explicit interface definitions (can transfer to simulation) – formal verification of RTL units, without vectors l System correctness at RTL level not guaranteed And note, this is not a highly automated process. . . 55

Summary l Basic specification and verification techniques – Temporal logic model checking – Finite automata – Symbolic simulation l Application at different levels – Local property verification – Abstract model verification – Local refinement verification l Benefits – Find design errors (negative results) – Make assumptions explicit – Systematically rule out classes of design errors 56