Part 3 The Data Link Layer 3 1

Part 3 The Data Link Layer 3. 1 Framing & Error Control 3. 2 Error & Flow Control University of Calgary CS 441 1

3. 1 Framing & Error Control • Asynchronous Character Transmission • Synchronous Frame Transmission • Error Detection • Hamming Distance • Cyclic Redundancy Checks • CRC Implementation • Forward Error Control • Backward Error Control University of Calgary CS 441 2

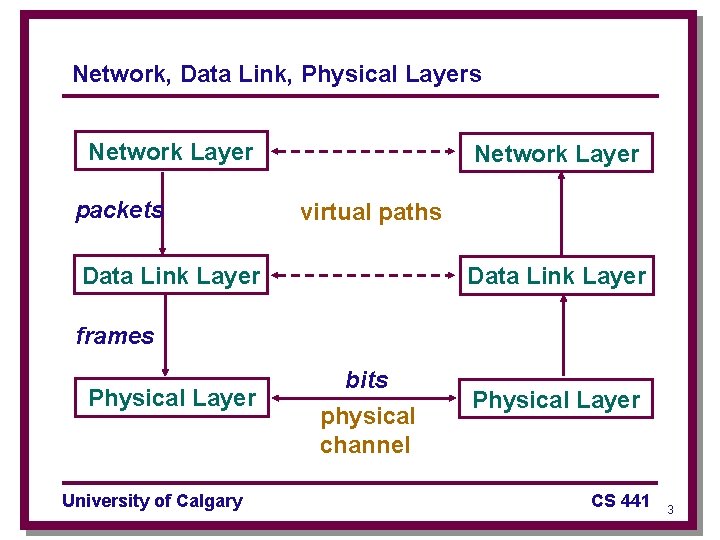
Network, Data Link, Physical Layers Network Layer packets Network Layer virtual paths Data Link Layer frames Physical Layer University of Calgary bits physical channel Physical Layer CS 441 3

Data Link Layer Requirements • Accept Packets from Network Layer on Host A and transfer to Network Layer on Host B • Transfer (Packets only) without errors • Deliver Packets in the order received • Deliver one and only one copy of each Packet • If errors are rare this may not be efficient, i. e. , the overhead associated with reliable transfer • Higher Layers can deal with end to end errors University of Calgary CS 441 4

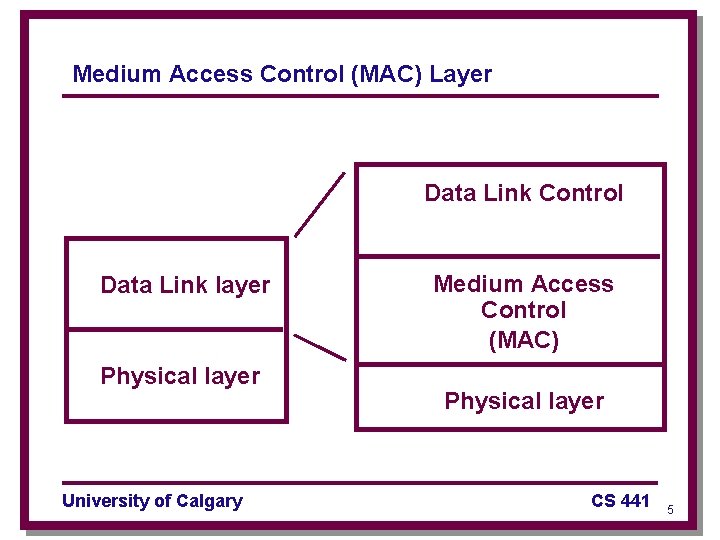
Medium Access Control (MAC) Layer Data Link Control Data Link layer Physical layer University of Calgary Medium Access Control (MAC) Physical layer CS 441 5

Point to Point • Establishment - ENQ (enquiry), ACK, NAC, ERP (error procedure) • Data Transfer • Termination - EOT ENQ A ACK B frame ACK University of Calgary CS 441 6

Asynchronous Character Transmission • data transmission one character at a time • otherwise idle sending binary 1, NRZ-L -volts • start bit is transition to 0 • then 7 bit ASCII followed by parity bit • final is a stop bit, a binary 1, for 1, 1. 5, or 2 times the normal bit duration • receiver can be easily synchronized • overhead of 2 -3 bits per character, ~2/9 = 22% University of Calgary CS 441 7

Synchronous Frame Transmission • block or frame transmission ~1000 bits • character/byte oriented frame is >= 1 synch characters; control characters; data characters; control characters • bit oriented frame is 8 bit flag, control field, data, control field, 8 bit flag • bit stuffing needed for the latter • in HDLC have 48 bits of control & flags which for 1000 bit message gives 4. 6% overhead University of Calgary CS 441 8

Framing • Physical Layer transfers bits unreliably • Framing enables efficient error control and synchronization on a bunch of bits • Could insert number of characters in header • Errors again make it very hard to resynchronize, where is start of next frame if an error? • Can deal with by using DLE STX and DLE ETX frame start and stop characters • Disadvantage with this method is that its closely tied to 8 bit characters and to ASCII. University of Calgary CS 441 9

Framing - Character Stuffing • frame starts with ASCII characters DLE STX • frame ends with ASCII characters DLE ETX + DLE: Data Link Escape + STX: Start of Text + ETX: End of Text • problem: ok for ASCII text, but binary data may have sequences matching these codes • solution: character stuffing + matches in data to DLE are "escaped" + sender inserts DLE before accidental one + receiver detects two DLE's, removes one University of Calgary CS 441 10

Framing - bit stuffing • Start and end a Frame with a flag byte : 01111110 • Whenever the sender sees five 1 s occur in a row in the data it inserts a 0 • Whenever the receiver sees five 1 s followed by a 0, it deletes the 0 • Bit stuffing is completely transparent to the Network Layer • Frames can be unambiguously recognized • When nothing to send can send flags University of Calgary CS 441 11

Errors in Physical Layer - Review • caused by + impulse noise + thermal noise + crosstalk + attenuation + frequency-dependent nature of - amplitude - propagation speed - phase + microwave interference, etc University of Calgary CS 441 12

Errors are Bursty • advantage: destroys occasional frames, rather than many frames + eg independent errors, with error rate of 0. 001 bits/sec, frame size = 1000 bits - average of one error per frame! + eg same error rate, but errors come in bursts of 100 - average error rate of 1 -2 frames/100 • disadvantage: harder to detect and correct, difficult to model mathematically University of Calgary CS 441 13

Coding Theory: Dealing with Errors • error detection + redundant (additional) information sent in a frame to allow receiver to detect errors • error correction + even more redundancy to allow errors to be detected and then corrected • codeword: + a frame with m (message) data bits and r (redundant) check bits and n = m + r total bits University of Calgary CS 441 14

Hamming Distance • the bit difference d between two code words, - algorithm: Exclusive OR two code words, count the 1 bits in the result - 1 0 0 1 1 0 1 code word 1 - 1 1 0 0 1 code word 2 - 0 1 0 0 0 X-OR'd result, - Hamming distance = 2 University of Calgary CS 441 15

Hamming Distance • Hamming distance of complete code: + all 2**m possible data messages are legal + not all 2**n codewords are legal + h. d. of complete code: - find the minimum Hamming Distance between any two code words • this minimum Hamming Distance is the Hamming Distance of that complete code University of Calgary CS 441 16

Significance of Hamming Distance • d single-bit errors are required to convert one codeword to into another + if two legal code words differ by 2 bits, then there have to be at least 2 bits in error to accidentaly convert one to the other • to detect d errors requires a distance d+1 code + if the Hamming Distance of complete code is 3, all legal words differ by “at least” 3 bits + any legal codeword with only 2 bits in error cannot produce another (different) legal codeword University of Calgary CS 441 17

Significance of Hamming Distance, Cont’d • to correct d errors requires distance 2 d+1 code + consider code with 5 bit Hamming Distance, ie all legal codes differ by “at least” 5 bits + if 2 bit errors occur within a codeword - h. d. illegal codeword to original = 2 - h. d. illegal codeword to any other legal codeword >= 3 • therefore can recognize original code word University of Calgary CS 441 18

Example 1: error detection via parity bits • add single "parity" bit to data so that + # "1" bits in codeword is even (even parity), or + # "1" bits in codeword is odd (odd parity) - eg 2 bits data, 1 bit odd parity: • 100 • 001 • 010 • 111 • Hamming Distance = 2, therefore can detect all 1 bit errors University of Calgary CS 441 19

Example 2: error correction code • 4 valid codewords, Hamming Distance = 5 + 0000011111 + 1111100000 + 11111 + can guarantee to correct 2 errors - 2 bit error corrected: + 00000 ->0011000000, closest to 00000 - eg 3 bit error detected but not corrected: + 00000 ->0011100000, closest to 1111100000 University of Calgary CS 441 20

Forward Error Correction • corrects by detecting + single bit error in a code word + the error's position in the code word • uses theoretical minimum number of check bits required to correct single errors • can also be used to detect burst errors • forward error correction is much less efficient than detection and retransmission • forward error correction is used where retransmission is impractical, eg broadcast, satellite situations, deep space probes University of Calgary CS 441 21

Minimum check bits to correct single errors • m message bits, r check bits, n=m+r m • 2 legal messages have n illegal words at distance 1 (invert each bit in legal word) • thus dedicate n+1 code words to each legal message n m • total number of code words is 2 >=(n+1)2 • Hamming’s forward code achieved this limit + number the bits starting with 1 from left + bits that are powers of 2 are check bits + rest (3, 5, 6, 7, 9, . . . ) are message bits + each message bit = sum of powers of 2 + each check bit makes the sum of its appearances in message sums + self = even (or odd) University of Calgary CS 441 22

Example 3: Hamming forward error correction • • msg = 1001000 (3 rd=2+1, 7 th=4+2+1) 1 st = 1+1+self=1+1+0=0 (for even parity) 2 nd = 1+1+self=0 4 th = 1+self=1 8 th = self = 0 code = 0 0 1 1 0 0 0 0 receiver tests each check bit k (=1, 2, 4, . . . ) if wrong adds k to counter • if counter 0 then word correct else it contains the number of the incorrect bit • eg, if 2 & 4 bits wrong, counter = 6, then 6 th wrong University of Calgary CS 441 23

Hamming Forward Burst Error Correction • k codewords define k rows in a k by n matrix • instead of sending rows, send columns • collect the k columns at receiving end and reform the k by n matrix • if a burst error of length , =k occurs it will cause at most one error per word, => correctable • kr check bits for data blocks of size km enables correcting burst errors of up to k bits University of Calgary CS 441 24

Cyclic Redundancy Checks (CRC) • given m bit message M add R, an r bit frame checksum = frame of m+r = n bits = T • R, the r bit checksum, is the remainder of dividing M by G, a constant r+1 bit number • thus : + T = 2 r M + R + where R = remainder R of 2 r M/ G + then + T/ G = 2 r M/ G + R / G = Q + R/ G + R / G = Q • ie, if no remainder (T/G=Q) then correct • m must be greater than r University of Calgary CS 441 25

Review Modulo 2 Arithmetic • examples 1111 + 1010 = 0101 1111 - 1010 = 0101 1010 + 0101 = 1111 1010 - 0101 = 1111 11 * 11001 = 110010 + 11001 = 101011 101/ 11 = 11 remainder 0 11 * 11 = 11 + 110 = 101 University of Calgary CS 441 26

Example - M = 11011 & generator G = 1011 • compute R = remainder of (2 r M + 000)/G 11011000 / 1011 = 11111 + 001/ 1011 • thus T = 11011001/ 1011 = 11111 University of Calgary CS 441 27

Polynomial Arithmetic • 1011 = x 3 + x + 1 = M(x) • Generator G(x) = x 5 + x 3 + 1 = 101001 • still use modulo 2 arithmetic • G always of the form 1. . . 1 • CRC-16 = X 16 + X 15 + X 2 + 1 T(x) = xr M(x) + R(x) TR(x) = T(x) + E(x) where E = error pattern University of Calgary CS 441 28

CRC Error Detection • An error is undetectable IFF E divisible by G TR(x) = T(x) + E(x) TR(x)/G = T(x)/G(x) + E(x)/G(x) = Q + E(X)/G(x) • CRC-16=G(x)= X 16 + X 15 + X 2 + 1 = 11000000101 all single & double bit errors any odd number of errors if G(x) contains x+1 any burst error of length <= r = 16 99. 997% of 17 bit bursts 99. 998% of 18 bit and longer bursts University of Calgary CS 441 29

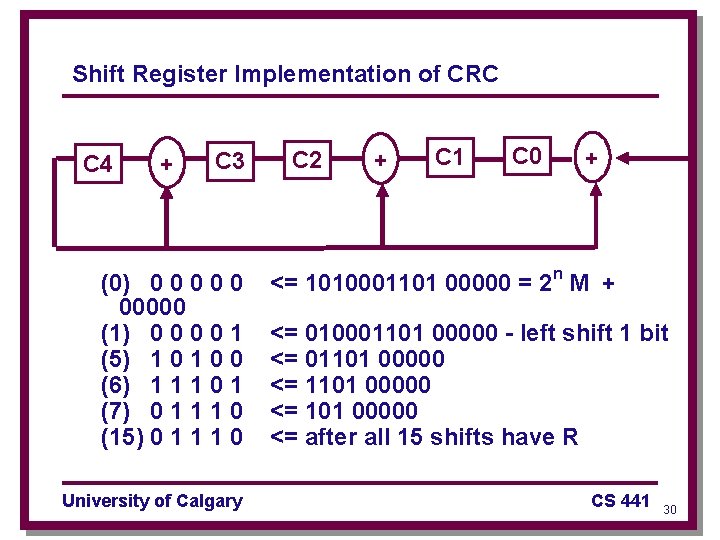
Shift Register Implementation of CRC C 4 + C 3 (0) 0 0 00000 (1) 0 0 1 (5) 1 0 0 (6) 1 1 1 0 1 (7) 0 1 1 1 0 (15) 0 1 1 1 0 University of Calgary C 2 + C 1 C 0 + <= 1010001101 00000 = 2 n M + <= 010001101 00000 - left shift 1 bit <= 01101 00000 <= after all 15 shifts have R CS 441 30

Receiver Implementation of CRC • have duplicate logic • received bits for M shifted into register • this should leave R in shift register • as the received R bits are shifted in they will zero out the register • if the register isn’t all zeros then an error has occured in TR /= T = 2 n M + R and E(X) /= 0 University of Calgary CS 441 31

Coding Theory • view legal code words as points in multidimensional space • want to develop complete codes with maximum Hamming Distance, idealy all are further apart than some minimum Hamming distance • can detect d errors if minimum Hamming Distance is d+1 • can correct d errors if minimum distance is 2 d+1 • forward error correction imposes this 2 d+1 overhead on every message • backward error correction incurs overhead to University of Calgary CS 441 retransmit which should be rare 32