Part 3 Linear Programming 3 5 Flows in

The Transportation Model (A Special Case of Transshipment Model)

Transshipment Problem The transportation problem is a special case of the minimum cost flow

Problem Structure The coefficient matrix A of the flow constraints is the node-arc incidence

Spanning Tree • A graph is connected if there is a chain between any

Structure of a Basis • The is a direct one-to-one correspondence between the arcs

Slides: 14

Download presentation

Part 3 Linear Programming 3. 5 Flows in Networks

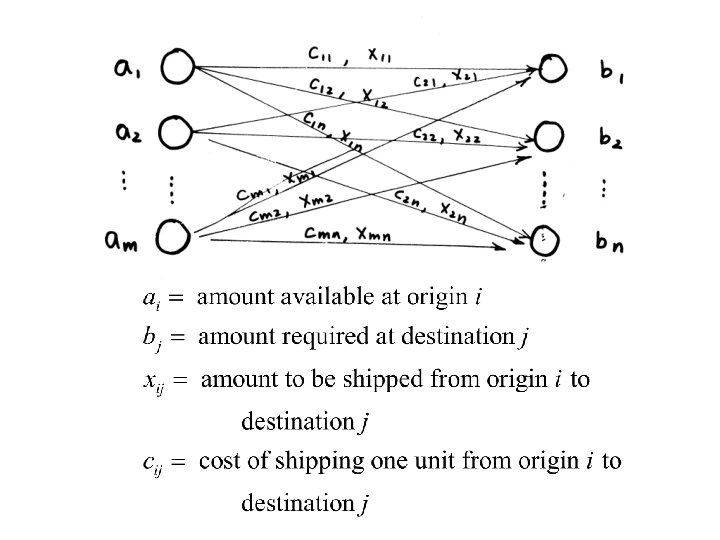
The Transportation Model (A Special Case of Transshipment Model)

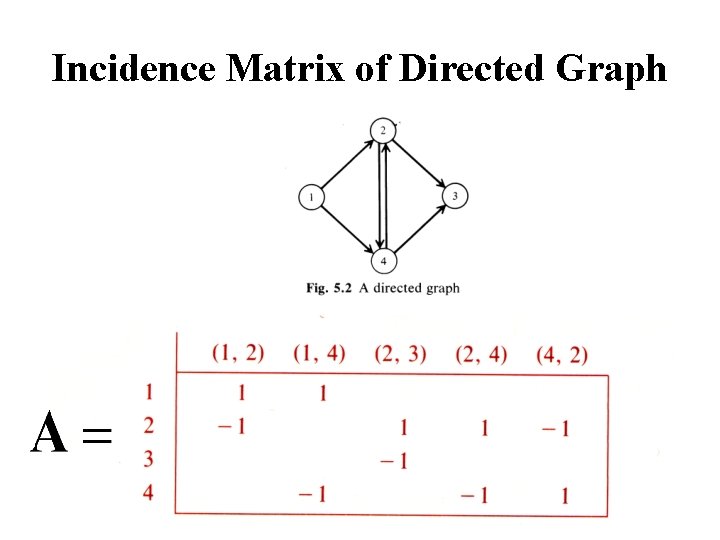
Incidence Matrix of Directed Graph

Material Balance Around a Node

Minimum Cost Flow Problem

Transshipment Problem The transportation problem is a special case of the minimum cost flow problem, corresponding to a network with arcs going only from supply nodes (origins) to demand nodes (destinations). The more general problem allows for arbitrary network configuration, so that flow from a supply node may progress through several intermediate nodes before reaching its destination. The more general problem is often termed the transshipment problem.

Problem Structure The coefficient matrix A of the flow constraints is the node-arc incidence matrix of the network. The column corresponding to arc (i, j) has a +1 entry in row i and a -1 entry in row j. Since the sum of all rows of A is the zero vector, the matrix A has a rank of at most n-1.

Incidence Matrix of Directed Graph

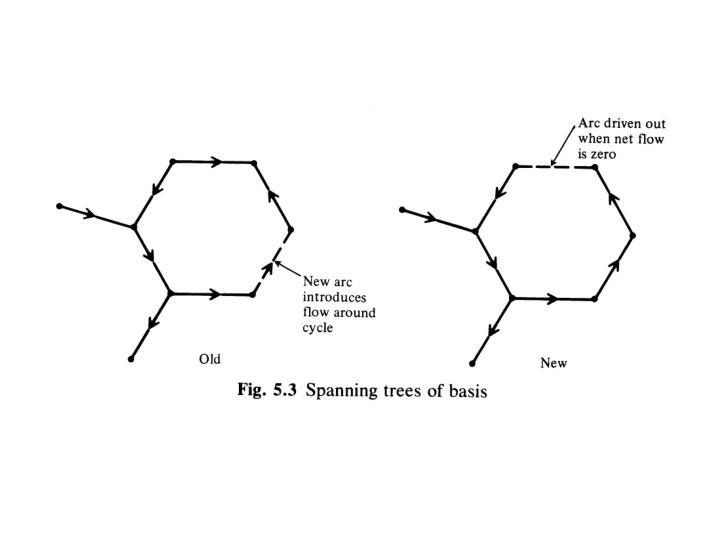
Spanning Tree • A graph is connected if there is a chain between any two nodes. • A graph is a tree if it is connected and has no cycles. • Consider a tree within a graph G which is made of a subset of arcs from G. Such a tree is a spanning tree if it touches all nodes of G. • A graph is connected iff it contains a spanning tree.

Structure of a Basis • The is a direct one-to-one correspondence between the arcs in a basis and a spanning tree. • Any basis (i. e. , spanning tree) is triangular. • Given a basis, the corresponding basic solution can be found by back substitution using the triangular structure. • In terms of network concepts, one first look for an end of the spanning tree corresponding to the basis, i. e. , an node touched by only one arc of the tree. The flow in this arc is then determined by the supply or demand at the node. • Back substitution corresponds to solving for flows along the arcs of the spanning tree, starting from an end and successively eliminating arcs.

The Simplex Method

Step 3