Part 3 Linear Programming 3 4 Transportation Problem

Part 3 Linear Programming 3. 4 Transportation Problem

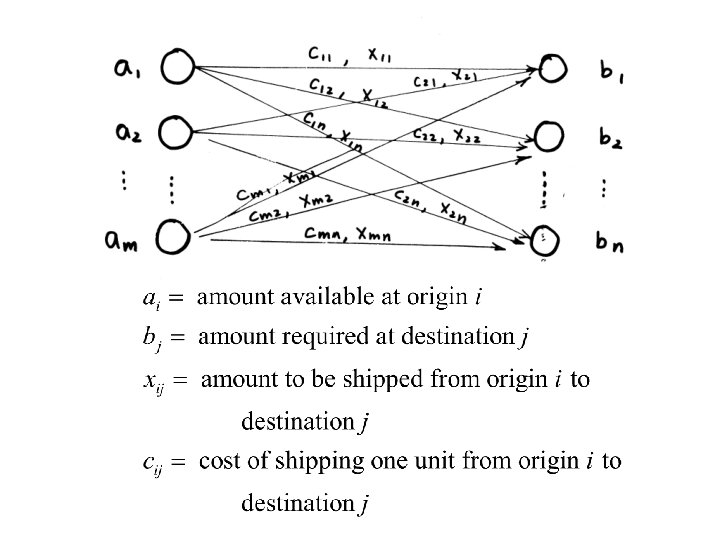
The Transportation Model

Theorem A transportation problem always has a solution, but there is exactly one redundant equality constraint. When any one of the equality constraints is dropped, the remaining system of n+m-1 equality constraints is linearly independent.

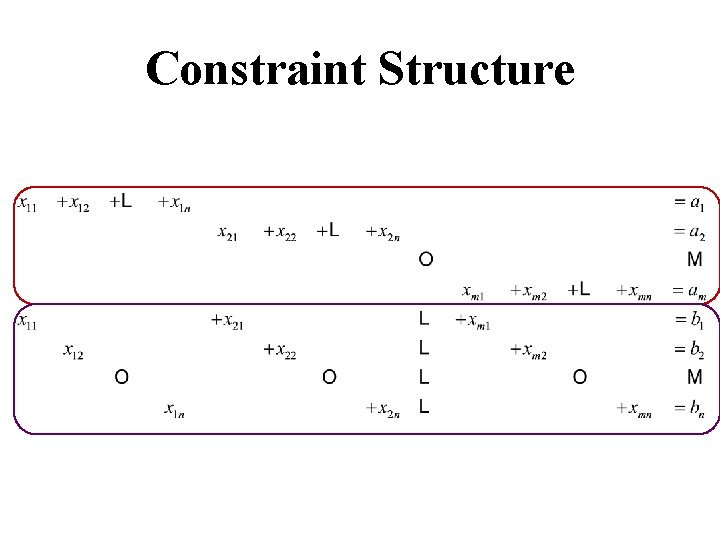
Constraint Structure

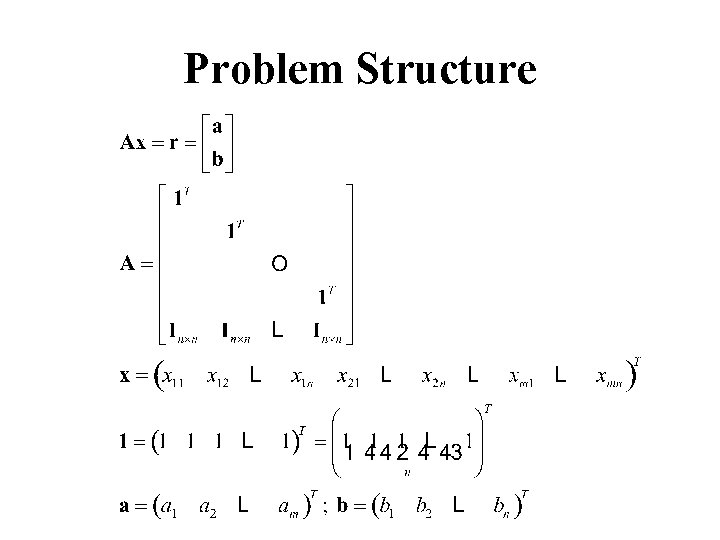
Problem Structure

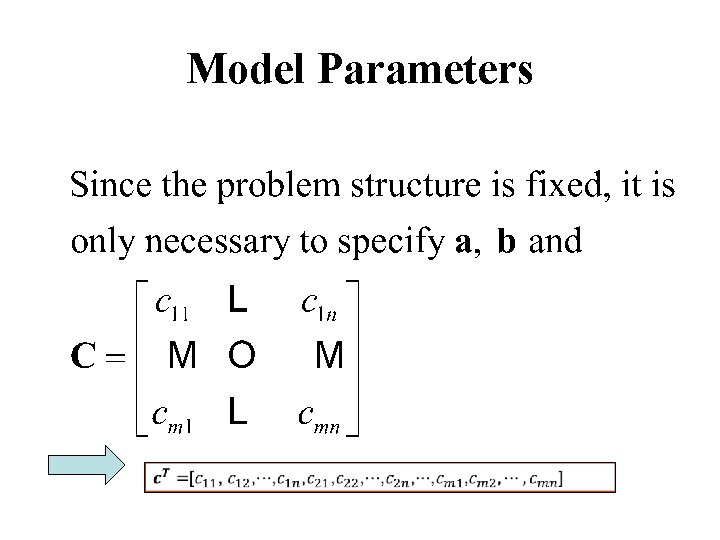
Model Parameters

Alternative Form of Duality

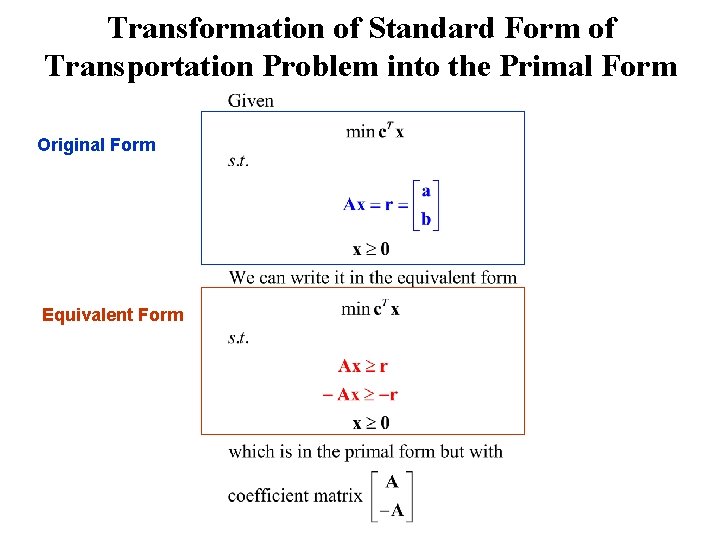
Transformation of Standard Form of Transportation Problem into the Primal Form Original Form Equivalent Form

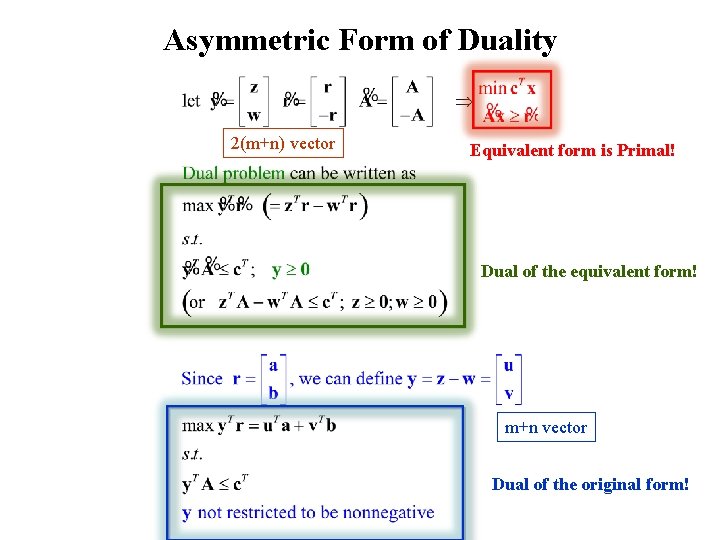
Asymmetric Form of Duality 2(m+n) vector Equivalent form is Primal! Dual of the equivalent form! m+n vector Dual of the original form!

Dual Transportation Problem

Interpretation of the Dual Transportation Problem •

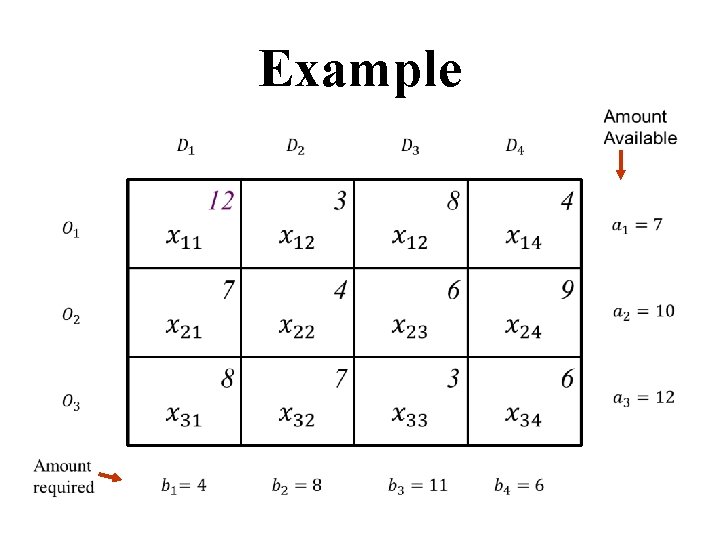
Example

Solution Procedure • Step 1: Set up the solution table. • Step 2: “Northwest Corner Rule” – when a cell is selected for assignment, the maximum possible value must be assigned in order to have a basic feasible solution for the primal problem (but may not be the optimal solution).

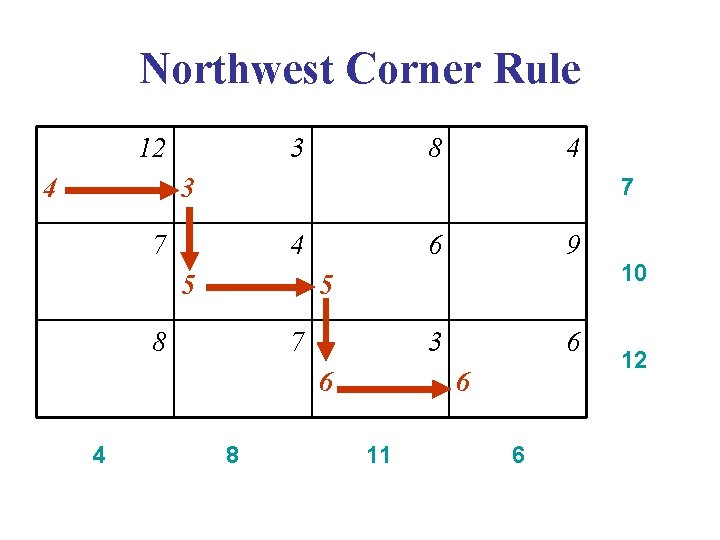
Northwest Corner Rule 12 4 3 8 4 3 7 7 4 5 9 3 6 5 8 7 6 4 6 8 6 11 6 10 12

Triangular Matrix • Definition: A nonsingular square matrix M is said to be triangular if by a permutation of its rows and columns it can be put in the form of a lower triangular matrix. • Clearly a nonsingular lower triangular matrix is triangular according to the above definition. • A nonsingular upper triangular matrix is also triangular, since by reversing the order of its rows and columns it becomes lower triangular.

How to determine if a given matrix is triangular? 1. Find a row with exactly one nonzero entry. 2. Form a submatrix of the matrix used in Step 1 by crossing out the row found in Step 1 and the column corresponding to the nonzero entry in that row. 3. Return to step 1 with this submatrix. If this procedure can be continued until all rows have been eliminated, then the matrix is triangular.

The importance of triangularity is the associated method of back substitution in solving

Basis Triangularity • Basis Triangularity Theorem: Every basis of the transportation problem is triangular.

Additional Insights

Step 3: Find a basic feasible solution of the dual problem – initial guess Due to one of the constraints in the primal problem is redundant!

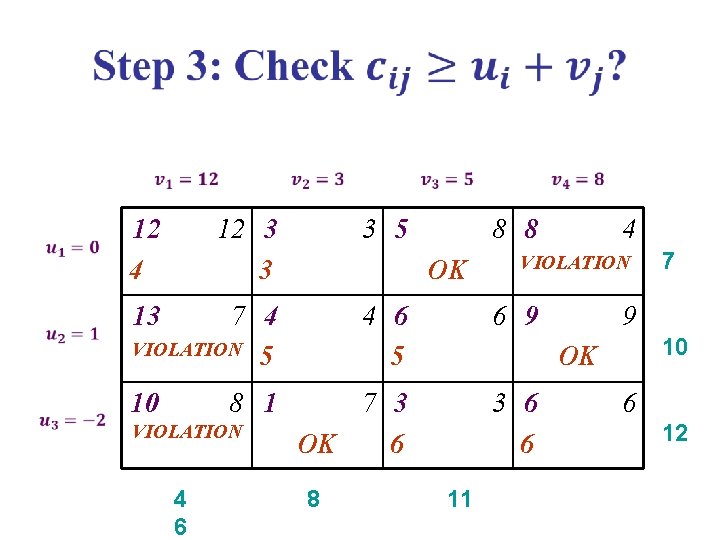
12 4 12 3 3 3 5 7 4 VIOLATION 5 4 6 5 6 9 7 3 OK 6 3 6 6 OK 13 10 8 1 VIOLATION 4 6 8 8 8 4 VIOLATION 9 10 OK 11 7 6 12

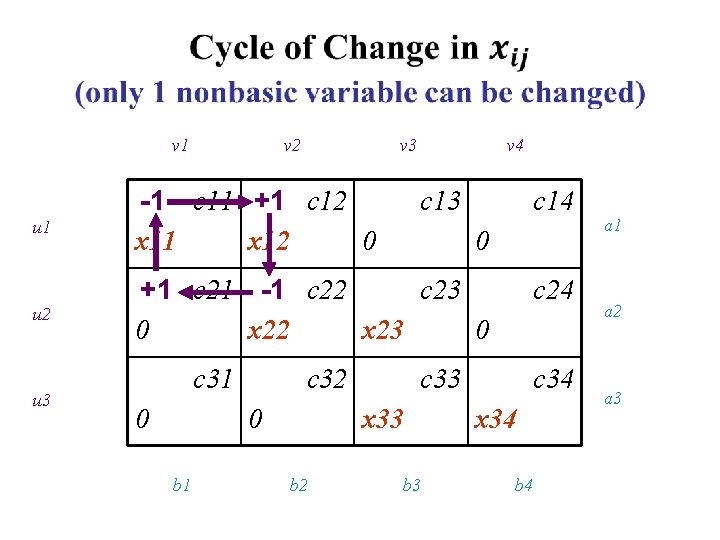
v 1 v 2 v 3 v 4 u 1 -1 c 11 +1 c 12 x 11 x 12 0 u 2 +1 c 21 -1 c 22 c 23 0 x 22 x 23 0 u 3 c 31 0 b 1 c 13 0 c 32 0 c 24 c 33 x 33 b 2 c 14 b 3 c 34 x 34 b 4 a 1 a 2 a 3

Selection of New Basic Variable

Step 4: Find a basic feasible solution of the dual problem – Loop identification

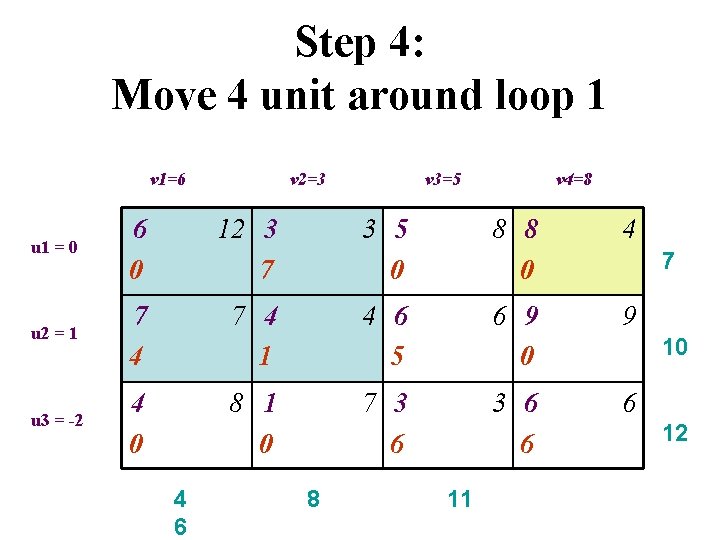
Step 4: Move 4 unit around loop 1 v 1=6 v 2=3 v 3=5 v 4=8 u 1 = 0 6 0 12 3 7 3 5 0 8 8 0 4 u 2 = 1 7 4 1 4 6 5 6 9 0 9 u 3 = -2 4 0 8 1 0 7 3 6 6 6 4 6 8 11 7 10 12

Repeat Step 3 Violation: Cell 14

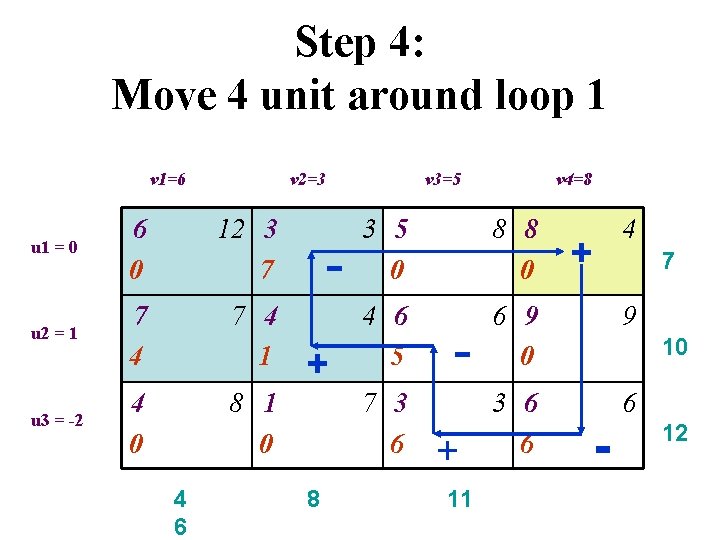
Step 4: Move 4 unit around loop 1 v 1=6 v 2=3 u 1 = 0 6 0 12 3 7 u 2 = 1 7 4 1 u 3 = -2 4 0 8 1 0 4 6 + v 3=5 3 5 0 8 8 0 4 6 5 6 9 0 9 3 6 6 6 7 3 6 8 v 4=8 + 11 + 4 7 10 - 12

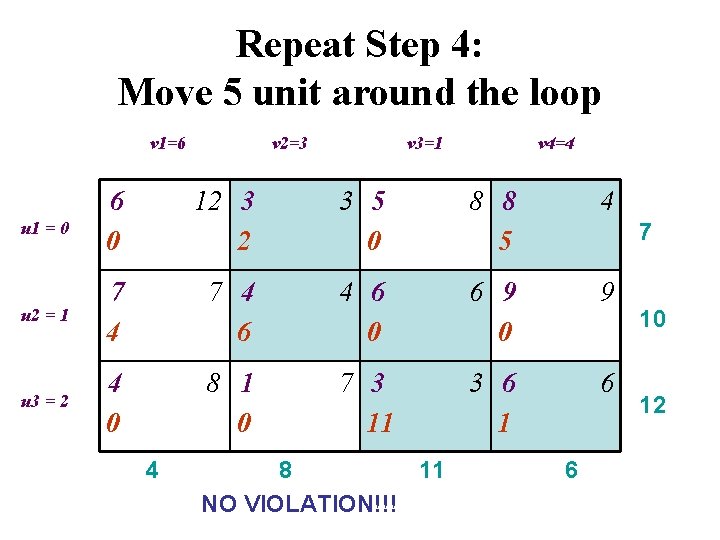
Repeat Step 4: Move 5 unit around the loop v 1=6 v 2=3 v 3=1 v 4=4 12 3 5 0 8 8 5 4 u 1 = 0 6 0 u 2 = 1 7 4 6 4 6 0 6 9 0 9 u 3 = 2 4 0 8 1 0 7 3 11 3 6 1 6 4 8 11 NO VIOLATION!!! 7 6 10 12

Solution

Application – Minimum Utility Consumption Rates and Pinch Points Cerda, J. , and Westerberg, A. W. , “Synthesizing Heat Exchanger Networks Having Restricted Stream/Stream Matches Using Transportation Formulation, ” Chemical Engineering Science, 38, 10, pp. 1723 – 1740 (1983).

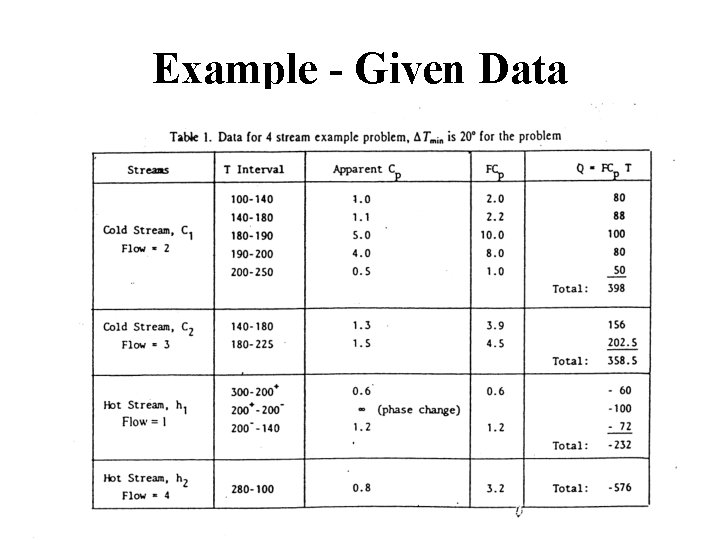
Example - Given Data

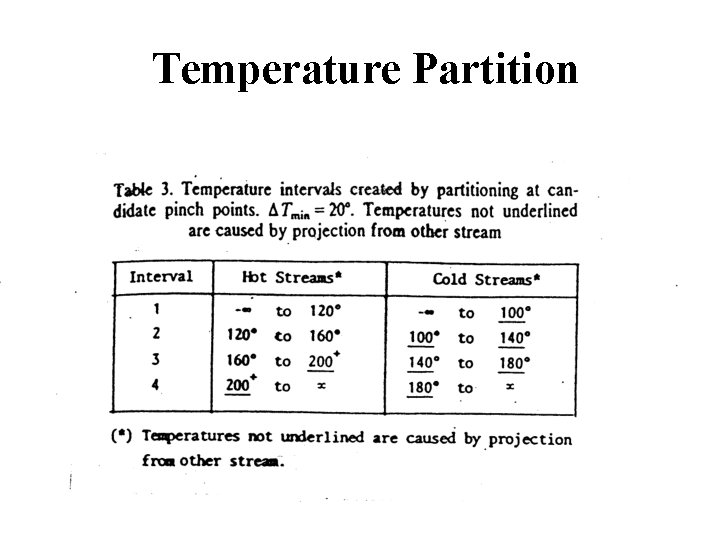
Temperature Partition

Definitions

Transportation Formulation

Cost Coefficients

Additional Constraints

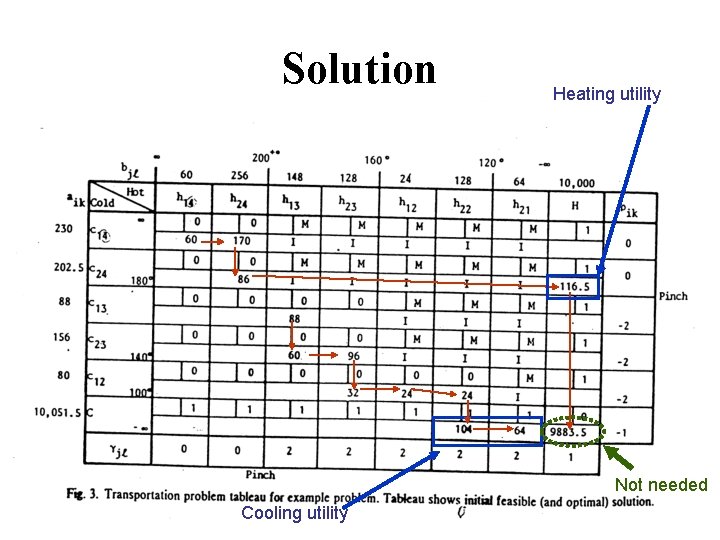
Solution Heating utility Not needed Cooling utility