Part 3 Image Classification using Sparse Coding Advanced

Part 3: Image Classification using Sparse Coding: Advanced Topics Kai Yu Andrew Ng Dept. of Media Analytics Computer Science Dept. NEC Laboratories America Stanford University 1

Outline of Part 3 • Why can sparse coding learn good features? - Intuition, topic model view, and geometric view - A theoretical framework: local coordinate coding - Two practical coding methods • Recent advances in sparse coding for image classification 12/18/2021 2

Outline of Part 3 • Why can sparse coding learn good features? - Intuition, topic model view, and geometric view - A theoretical framework: local coordinate coding - Two practical coding methods • Recent advances in sparse coding for image classification 12/18/2021 3

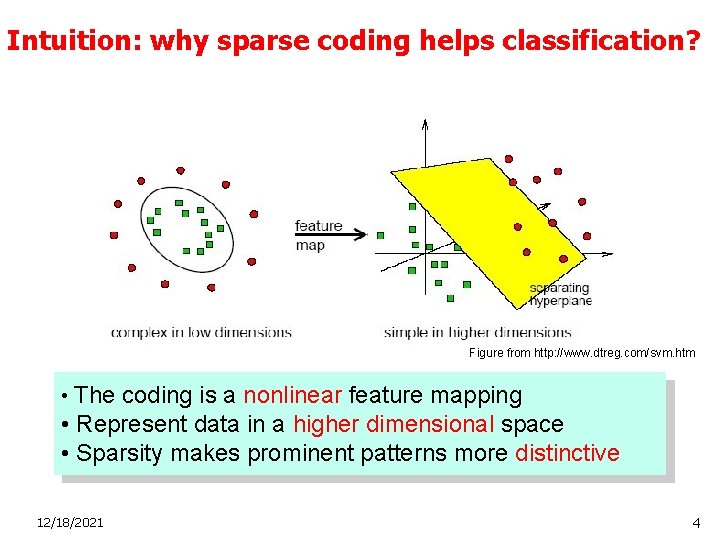
Intuition: why sparse coding helps classification? Figure from http: //www. dtreg. com/svm. htm • The coding is a nonlinear feature mapping • Represent data in a higher dimensional space • Sparsity makes prominent patterns more distinctive 12/18/2021 4

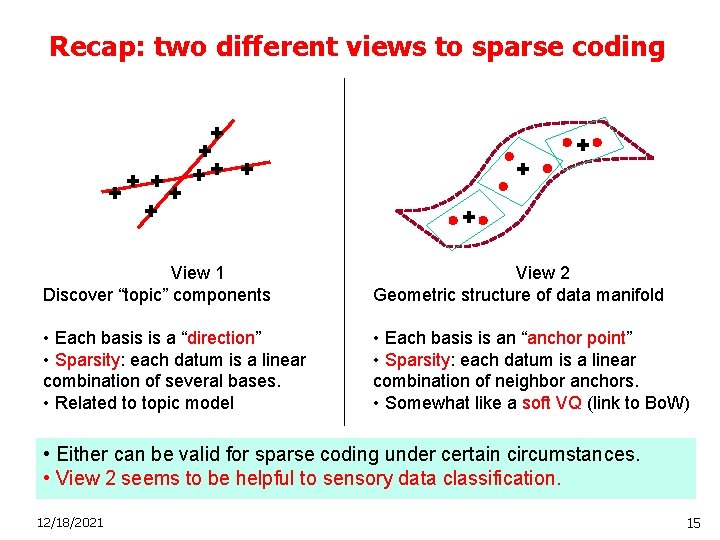
A “topic model” view to sparse coding Basis 1 Basis 2 Both figures adapted from CVPR 10 tutorial by F. Bach, J. Mairal, J. Ponce and G. Sapiro • Each basis is a “direction” or a “topic”. • Sparsity: each datum is a linear combination of only a few bases. • Applicable to image denoising, inpainting, and super-resolution. 12/18/2021 5

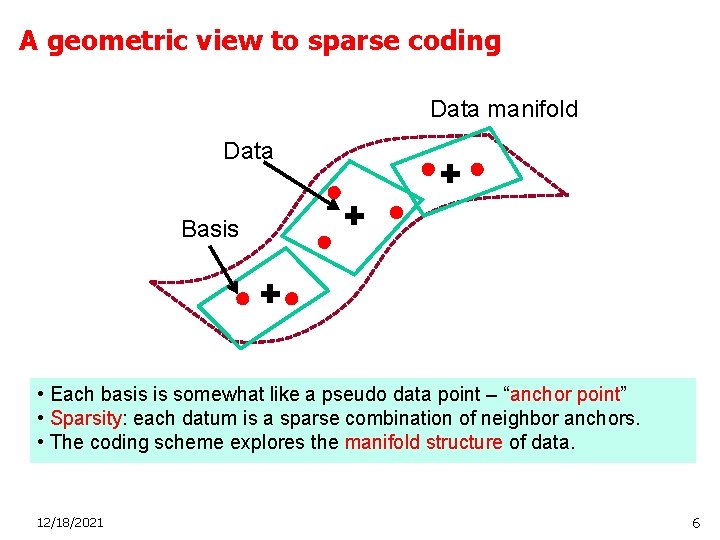
A geometric view to sparse coding Data manifold Data Basis • Each basis is somewhat like a pseudo data point – “anchor point” • Sparsity: each datum is a sparse combination of neighbor anchors. • The coding scheme explores the manifold structure of data. 12/18/2021 6

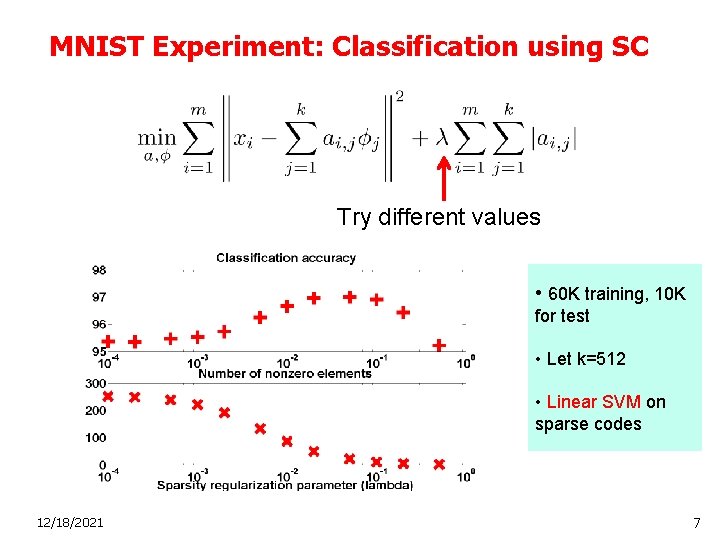
MNIST Experiment: Classification using SC Try different values • 60 K training, 10 K for test • Let k=512 • Linear SVM on sparse codes 12/18/2021 7

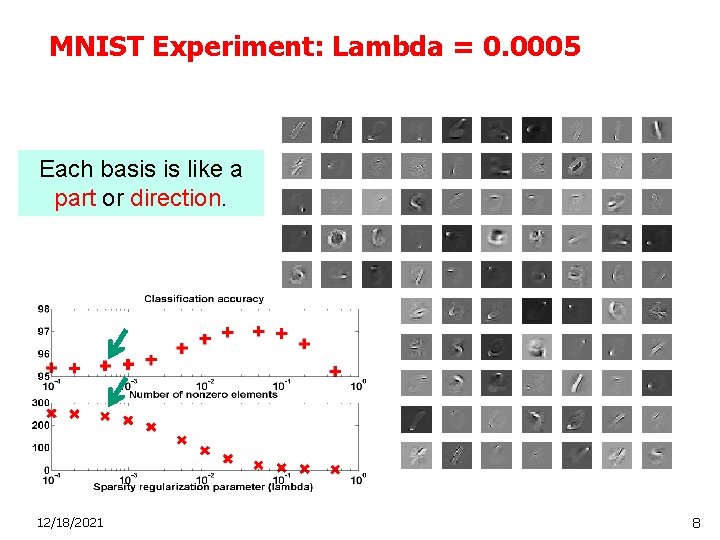
MNIST Experiment: Lambda = 0. 0005 Each basis is like a part or direction. 12/18/2021 8

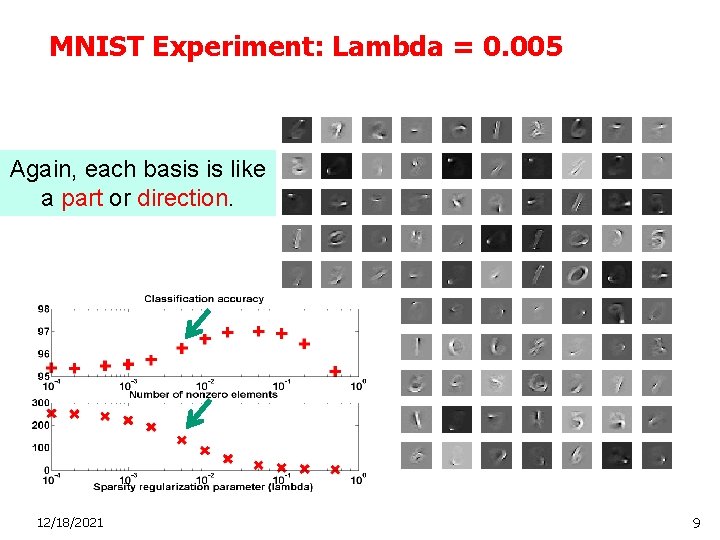
MNIST Experiment: Lambda = 0. 005 Again, each basis is like a part or direction. 12/18/2021 9

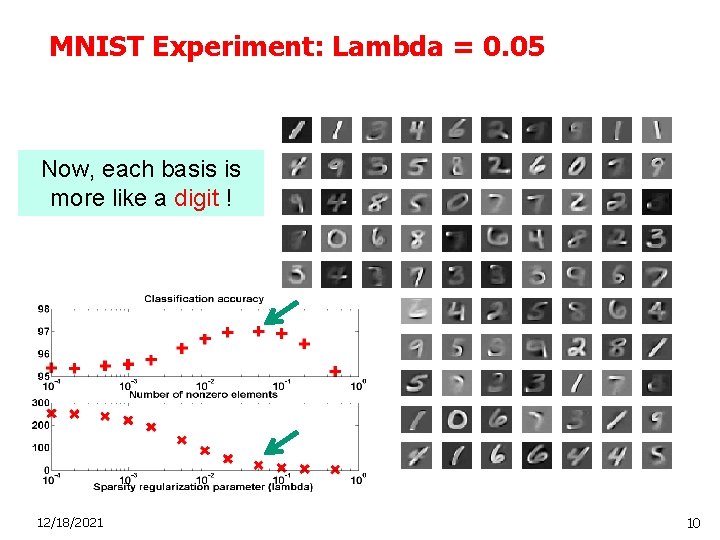
MNIST Experiment: Lambda = 0. 05 Now, each basis is more like a digit ! 12/18/2021 10

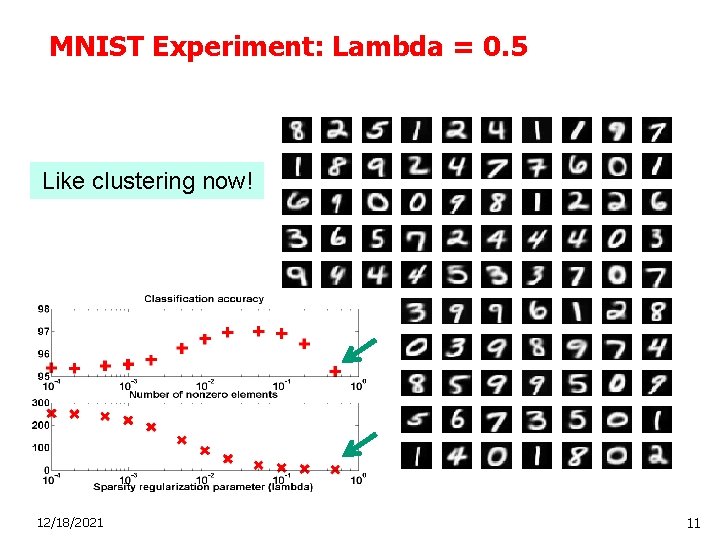
MNIST Experiment: Lambda = 0. 5 Like clustering now! 12/18/2021 11

Geometric view of sparse coding Error: 4. 54% Error: 3. 75% Error: 2. 64% • When SC achieves the best classification accuracy, the learned bases are like digits – each basis has a clear local class association. • Implication: exploring data geometry may be useful for classification. 12/18/2021 12

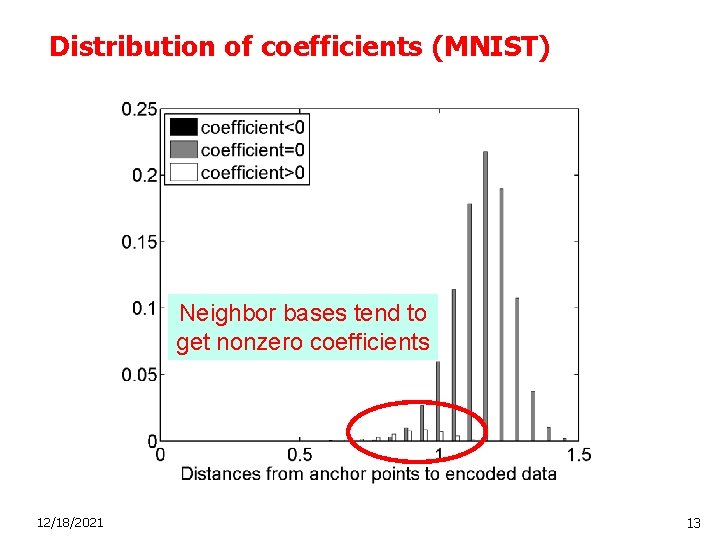
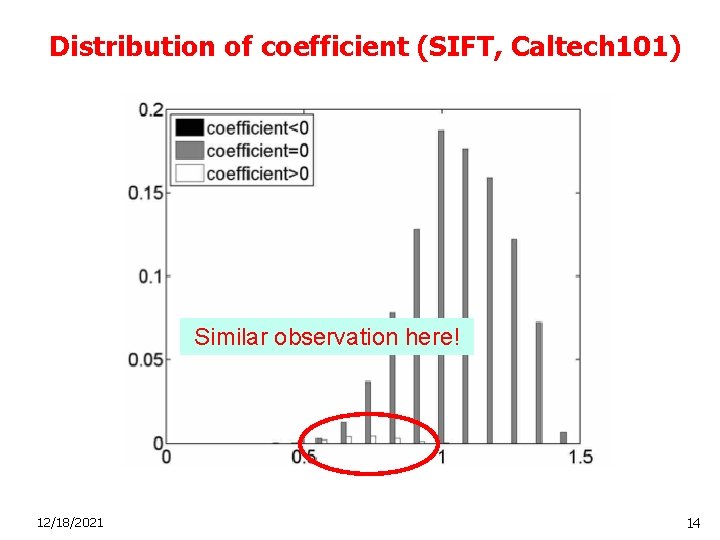
Distribution of coefficients (MNIST) Neighbor bases tend to get nonzero coefficients 12/18/2021 13

Distribution of coefficient (SIFT, Caltech 101) Similar observation here! 12/18/2021 14

Recap: two different views to sparse coding View 1 Discover “topic” components View 2 Geometric structure of data manifold • Each basis is a “direction” • Sparsity: each datum is a linear combination of several bases. • Related to topic model • Each basis is an “anchor point” • Sparsity: each datum is a linear combination of neighbor anchors. • Somewhat like a soft VQ (link to Bo. W) • Either can be valid for sparse coding under certain circumstances. • View 2 seems to be helpful to sensory data classification. 12/18/2021 15

Outline of Part 3 • Why can sparse coding learn good features? - Intuition, topic model view, and geometric view - A theoretical framework: local coordinate coding - Two practical coding methods • Recent advances in sparse coding for image classification 12/18/2021 16

Key theoretical question Cla ss ifica tion Fea lea ture rnin g • Why unsupervised feature learning via sparse coding can help classification? 12/18/2021 17

The image classification setting for analysis Dense local feature Implication: Sparse Coding Learning an image classifier is a matter of learning nonlinear functions on patches. Linear Pooling Linear SVM Function on images Function on patches

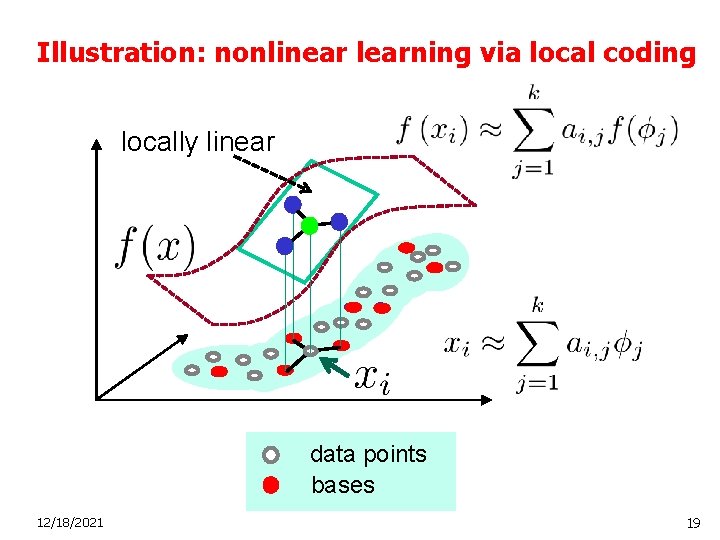
Illustration: nonlinear learning via local coding locally linear data points bases 12/18/2021 19

How to learn a nonlinear function? Step 1: Learning the dictionary from unlabeled data 12/18/2021

How to learn a nonlinear function? Step 2: Use the dictionary to encode data 12/18/2021

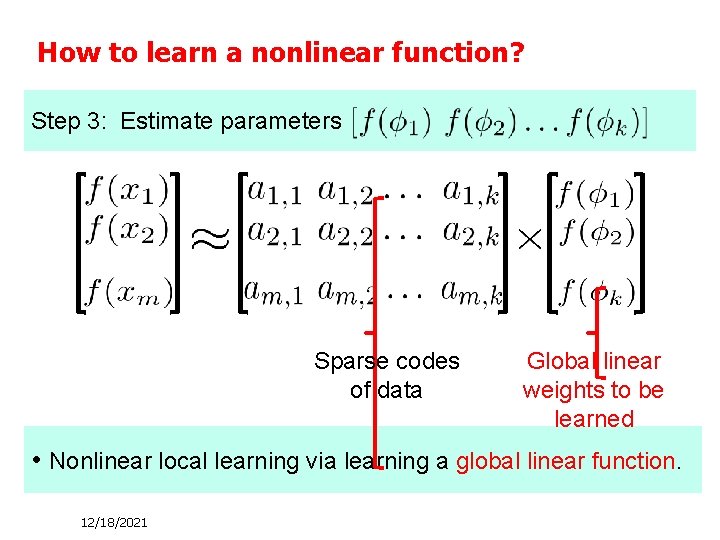
How to learn a nonlinear function? Step 3: Estimate parameters Sparse codes of data Global linear weights to be learned • Nonlinear local learning via learning a global linear function. 12/18/2021

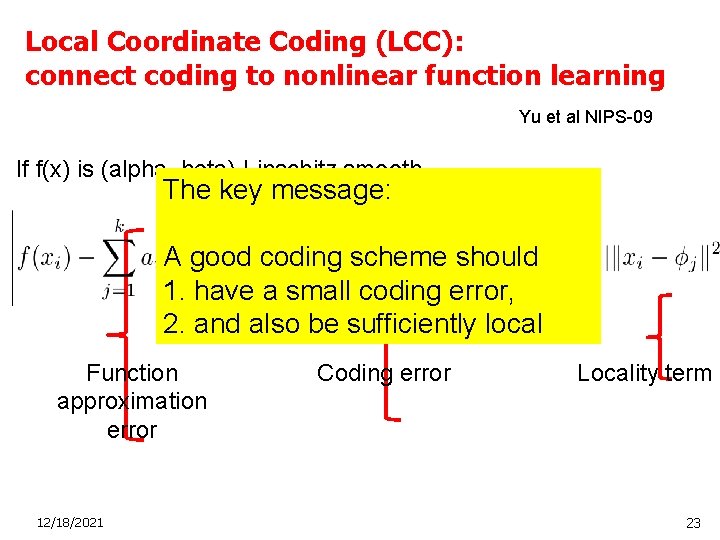
Local Coordinate Coding (LCC): connect coding to nonlinear function learning Yu et al NIPS-09 If f(x) is (alpha, beta)-Lipschitz smooth The key message: A good coding scheme should 1. have a small coding error, 2. and also be sufficiently local Function approximation error 12/18/2021 Coding error Locality term 23

Outline of Part 3 • Why can sparse coding learn good features? - Intuition, topic model view, and geometric view - A theoretical framework: local coordinate coding - Two practical coding methods • Recent advances in sparse coding for image classification 12/18/2021 24

Application of LCC theory • Fast Implementation with a large dictionary Wang et al, CVPR 10 • A simple geometric way to improve Bo. W Zhou et al, ECCV 10 12/18/2021 25

Application of LCC theory • Fast Implementation with a large dictionary • A simple geometric way to improve Bo. W 12/18/2021 26

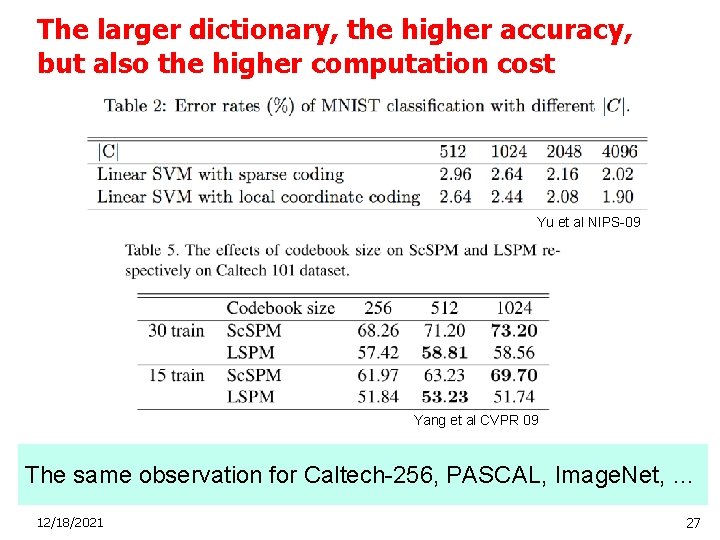
The larger dictionary, the higher accuracy, but also the higher computation cost Yu et al NIPS-09 Yang et al CVPR 09 The same observation for Caltech-256, PASCAL, Image. Net, … 12/18/2021 27

Locality-constrained linear coding a fast implementation of LCC Wang et al, CVPR 10 • Dictionary Learning: k-means (or hierarchical k-means) • Coding for X, Step 1 – ensure locality: find the K nearest bases Step 2 – ensure low coding error: 12/18/2021 28

Competitive in accuracy, cheap in computation Comparable with sparse coding Sparse coding This is one of the two major algorithms applied by NEC-UIUC team to achieve the No. 1 position in Image. Net challenge 2010! Significantly better than sparse coding Wang et al CVPR 10 12/18/2021 29

Application of the LCC theory • Fast Implementation with a large dictionary • A simple geometric way to improve Bo. W 12/18/2021 30

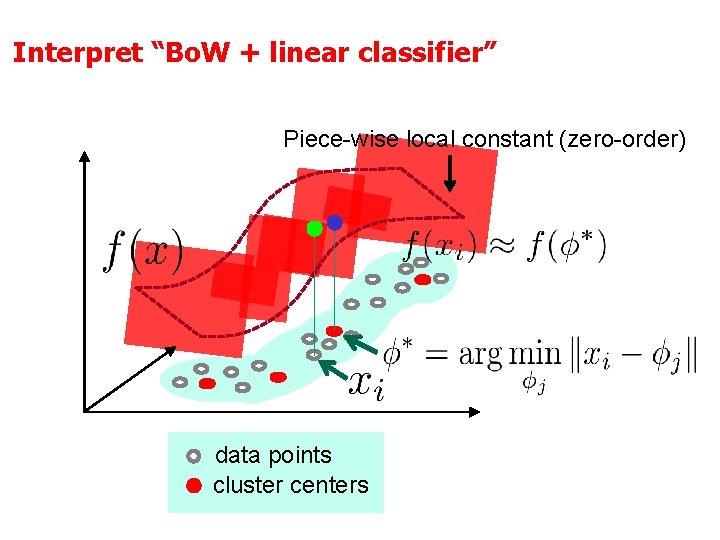
Interpret “Bo. W + linear classifier” Piece-wise local constant (zero-order) data points cluster centers

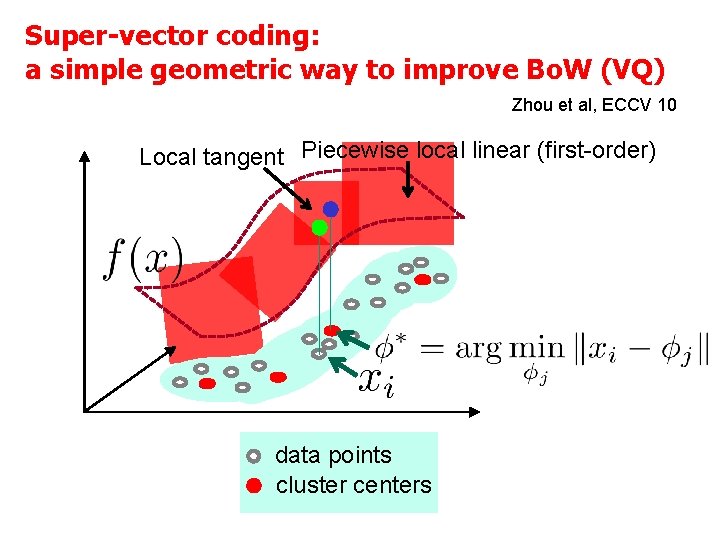
Super-vector coding: a simple geometric way to improve Bo. W (VQ) Zhou et al, ECCV 10 Local tangent Piecewise local linear (first-order) data points cluster centers

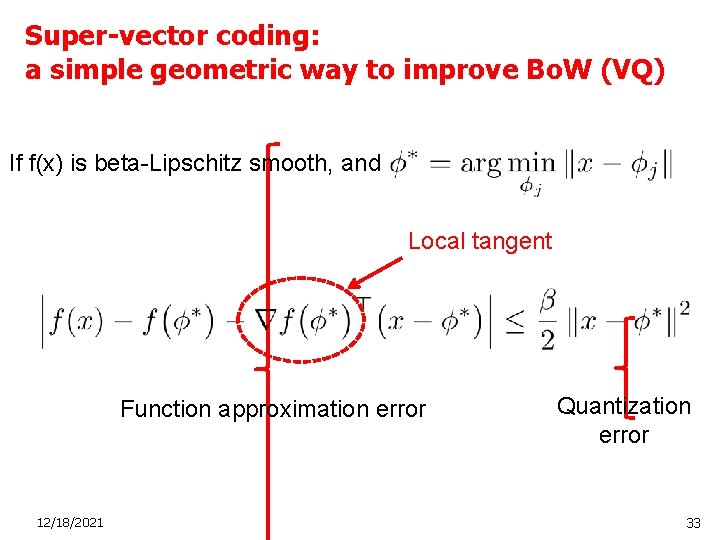
Super-vector coding: a simple geometric way to improve Bo. W (VQ) If f(x) is beta-Lipschitz smooth, and Local tangent Function approximation error 12/18/2021 Quantization error 33

Super-vector coding: learning nonlinear function via a global linear model Let be the VQ coding of This is one of the two major algorithms applied by NEC-UIUC team to achieve the No. 1 position in PASCAL VOC 2009! Super-vector codes of data 12/18/2021 Global linear weights to be learned

Summary of Geometric Coding Methods Vector Quantization (Fast) Local Coordinate (Bo. W) Coding Super-vector Coding • All lead to higher-dimensional, sparse, and localized coding • All explore geometric structure of data • New coding methods are suitable for linear classifiers. • Their implementations are quite straightforward.

Things not covered here • Improved LCC using Local Tangent, Yu & Zhang, ICML 10 • Mixture of Sparse Coding, Yang et al ECCV 10 • Deep Coding Network, Lin et al NIPS 10 • Pooling methods • Max-pooling works well in practice, but appears to be ad-hoc. • An interesting analysis on max-pooling, Boureau et al. ICML 2010 • We are working on a linear pooling method, which has a similar effect as max-pooling. Some preliminary results already in the super-vector coding paper, Zhou et al, ECCV 2010. 12/18/2021 36

Outline of Part 3 • Why can sparse coding learn good features? - Intuition, topic model view, and geometric view - A theoretical framework: local coordinate coding - Two practical coding methods • Recent advances in sparse coding for image classification 12/18/2021 37

Fast approximation of sparse coding via neural networks Gregor & Le. Cun, ICML-10 • The method aims at improving sparse coding speed in coding time, not training speed, potentially make sparse coding practical for video. • Idea: Given a trained sparse coding model, use its input outputs as training data to train a feed-forward model • They showed a speedup of X 20 faster. But not evaluated on real video data. 12/18/2021 38

Group sparse coding Bengio et al, NIPS 09 • Sparse coding is on patches, the image representation is unlikely sparse. • Idea: enforce joint sparsity via L 1/L 2 norm on sparse codes of a group of patches. • The resultant image representation becomes sparse, which can save the memory cost, but the classification accuracy decreases. 12/18/2021 39

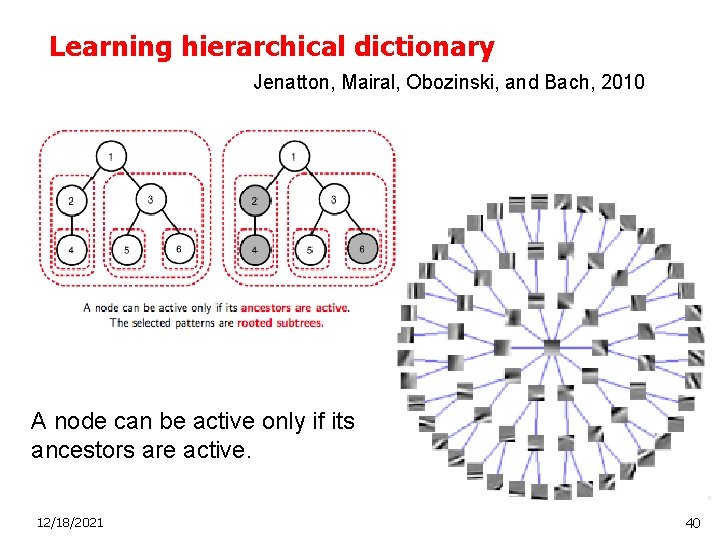
Learning hierarchical dictionary Jenatton, Mairal, Obozinski, and Bach, 2010 A node can be active only if its ancestors are active. 12/18/2021 40

Reference 1. Image Classification using Super-Vector Coding of Local Image Descriptors, Xi Zhou, Kai Yu, Tong Zhang, and Thomas Huang. In ECCV 2010. 2. Efficient Highly Over-Complete Sparse Coding using a Mixture Model, Jianchao Yang, Kai Yu, and Thomas Huang. In ECCV 2010. 3. Learning Fast Approximations of Sparse Coding, Karol Gregor and Yann Le. Cun. In ICML 2010. 4. Improved Local Coordinate Coding using Local Tangents, Kai Yu and Tong Zhang. In ICML 2010. 5. Sparse Coding and Dictionary Learning for Image Analysis, Francis Bach, Julien Mairal, Jean Ponce, and Guillermo Sapiro. CVPR 2010 Tutorial 6. Supervised translation-invariant sparse coding, Jianchao Yang, Kai Yu, and Thomas Huang, In CVPR 2010. 7. Learning locality-constrained linear coding for image classification, Jingjun Wang, Jianchao Yang, Kai Yu, Fengjun Lv, Thomas Huang, and Yihong Gong. In CVPR 2010. 8. Group Sparse Coding, Samy Bengio, Fernando Pereira, Yoram Singer, and Dennis Strelow, In NIPS*2009. 9. Nonlinear learning using local coordinate coding, Kai Yu, Tong Zhang, and Yihong Gong. In NIPS*2009. 10. Linear spatial pyramid matching using sparse coding for image classification, Jianchao Yang, Kai Yu, Yihong Gong, and Thomas Huang. In CVPR 2009. 11. Efficient sparse coding algorithms. Honglak Lee, Alexis Battle, Raina Rajat and Andrew Y. Ng. In NIPS*2007. 12/18/2021 41