Part 2 Schematic of the alcohol model Marginal

Part 2 • Schematic of the alcohol model • Marginal and conditional models • Variance components • Random Effects and Bayes • General, linear MLMs Term 4, 2006 BIO 656 --Multilevel Models 1

PLEASE DO THIS If you did not receive the welcome email from me, email me at: (tlouis@jhsph. edu) Term 4, 2006 BIO 656 --Multilevel Models 2

MULTI-LEVEL MODELS • Biological, physical, psycho/social processes that influence health occur at many levels: – Cell Organ Person Family Nhbd City Society . . . Solar system – Crew Vessel Fleet . . . – Block Group Tract . . . – Visit Patient Phy Clinic HMO . . . • Covariates can be at each level • Many “units of analysis” • More modern and flexible parlance and approach: “many variance components” Term 4, 2006 BIO 656 --Multilevel Models 3

Factors in Alcohol Abuse • Cell: neurochemistry • Organ: ability to metabolize ethanol • Person: genetic susceptibility to addiction • Family: alcohol abuse in the home • Neighborhood: availability of bars • Society: regulations; organizations; social norms Term 4, 2006 BIO 656 --Multilevel Models 4

ALCOHOL ABUSE A multi-level, interaction model • Interaction between prevalence/density of bars & state drunk driving laws • Relation between alcohol abuse in a family & ability to metabolize ethanol • Genetic predisposition to addiction • Household environment • State regulations about intoxication & job requirements Term 4, 2006 BIO 656 --Multilevel Models 5

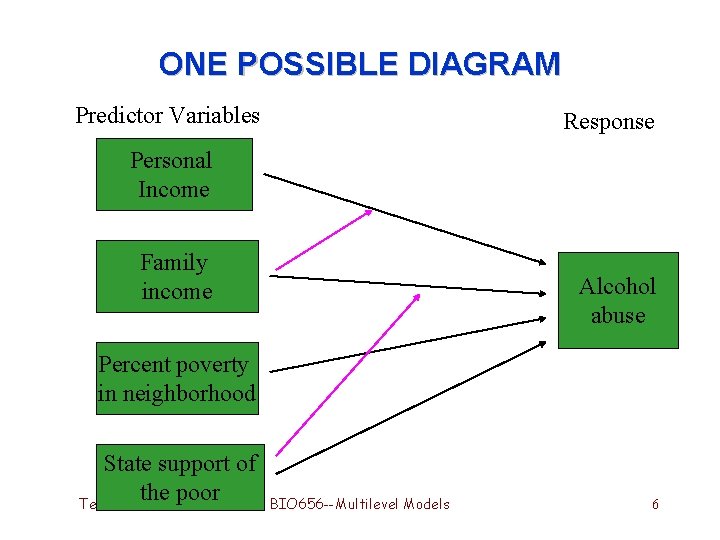
ONE POSSIBLE DIAGRAM Predictor Variables Response Personal Income Family income Alcohol abuse Percent poverty in neighborhood State support of the poor Term 4, 2006 BIO 656 --Multilevel Models 6

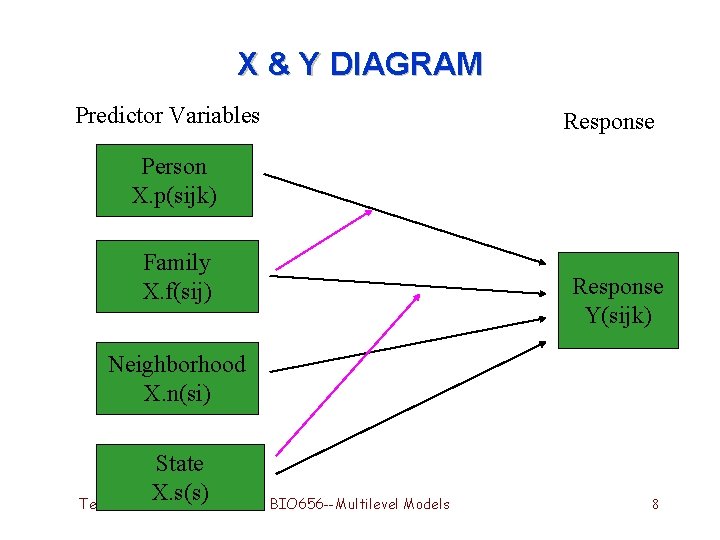
NOTATION (the Term 4, 2006 reverse order of what I usually use!) BIO 656 --Multilevel Models 7

X & Y DIAGRAM Predictor Variables Response Person X. p(sijk) Family X. f(sij) Response Y(sijk) Neighborhood X. n(si) State X. s(s) Term 4, 2006 BIO 656 --Multilevel Models 8

Standard Regression Analysis Assumptions Data follow normal distribution All the key covariates are included Xs are measured without error Responses are independent Term 4, 2006 BIO 656 --Multilevel Models 9

Non-independence (dependence) within-cluster correlation • Two responses from the same family (cluster) tend to be more similar than do two observations from different families • Two observations from the same neighborhood tend to be more similar than do two observations from different neighborhoods • Why? Term 4, 2006 BIO 656 --Multilevel Models 10

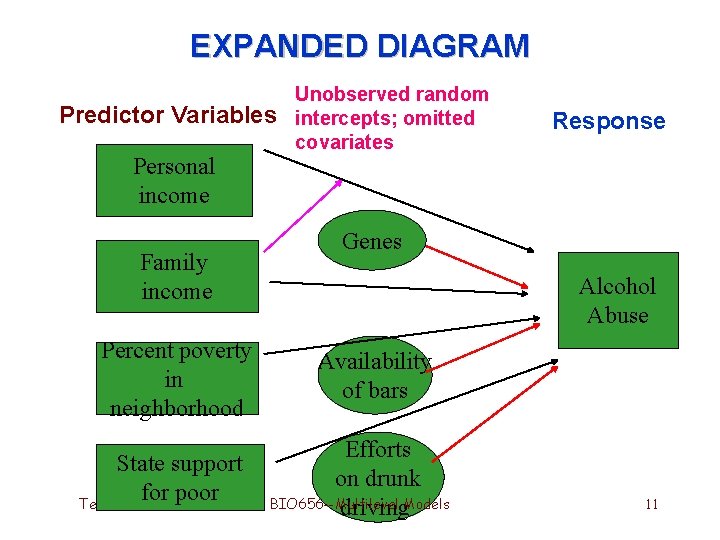
EXPANDED DIAGRAM Predictor Variables Personal income Family income Percent poverty in neighborhood State support for poor Term 4, 2006 Unobserved random intercepts; omitted covariates Response Genes Alcohol Abuse Availability of bars Efforts on drunk BIO 656 --Multilevel driving. Models 11

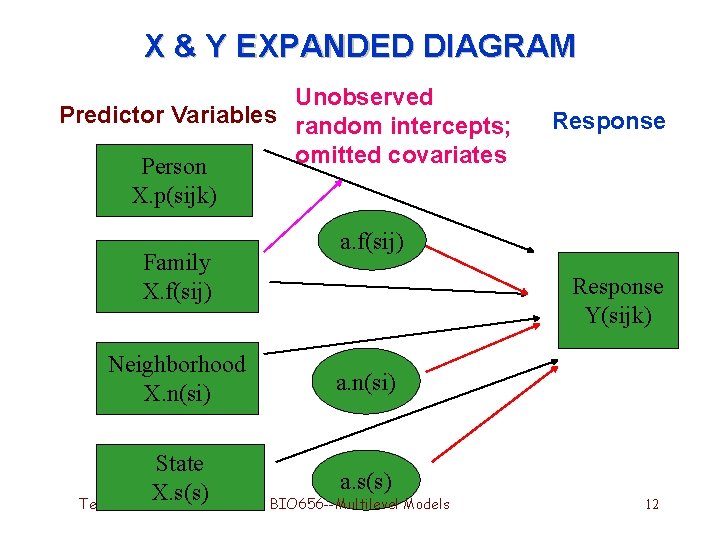
X & Y EXPANDED DIAGRAM Unobserved Predictor Variables random intercepts; omitted covariates Person X. p(sijk) Family X. f(sij) Neighborhood X. n(si) State X. s(s) Term 4, 2006 Response a. f(sij) Response Y(sijk) a. n(si) a. s(s) BIO 656 --Multilevel Models 12

Variance Inflation and Correlation induced by unmeasured or omitted latent effects • Alcohol usage for family members is correlated because they share an unobserved “family effect” via common – genes, diet, family culture, . . . • Repeated observations within a neighborhood are correlated because neighbors share common – traditions, access to services, stress levels, … • Including relevant covariates can uncover latent effects, reduce variance and correlation Term 4, 2006 BIO 656 --Multilevel Models 13

Key Components of a Multi-level Model • Specification of predictor variables (fixed effects) at multiple levels: the “traditional” model – Main effects and interactions at and between levels – With these, it’s already multi-level! • Specification of correlation among responses within a cluster – via Random effects and other correlation-inducers • Both the fixed effects and random effects specifications must be informed by scientific understanding, the research question and empirical evidence Term 4, 2006 BIO 656 --Multilevel Models 14

INFERENTIAL TARGETS Marginal mean or other summary “on the margin” • For specified covariate values, the average response across the population Conditional mean or other summary conditional on: • Other responses (conditioning on observeds) • Unobserved random effects Term 4, 2006 BIO 656 --Multilevel Models 15

Marginal Model Inferences Public Health Relevant • Features of the distribution of response averaged over the reference population – Mean response – Variance of the response distribution – Comparisons for different covariates Examples • Mean alcohol consumption for men compared to women • Rate of alcohol abuse for states with active addiction treatment programs versus states without – Association is not causation! Term 4, 2006 BIO 656 --Multilevel Models 16

Conditional Inferences Conditional on observeds or latent effects • Probability that a person abuses alcohol conditional on the number of family members who do • A person’s average alcohol consumption, conditional on the neighborhood average Warning • For conditional models, don’t put a LHS variable on the RHS “by hand” • Use the MLM to structure the conditioning Term 4, 2006 BIO 656 --Multilevel Models 17

The Warning Model: Yit = 0 + 1 smokingit + eij Don’t do this Yi(t+1) | Yit = 0 + 1 smokingit + Yit + e*i(t+1) Do this (better still, let probability theory do it) Yi(t+1) | Yit = 0 + 1 smokingi(t+1) + (Yit – 0 - 1 smokingit) + e**i(t+1) Because Unless you center the regressor, the smoking effect will not have a marginal model interpretation, will be attenuated, will depend on , won’t be “exportable, ”. . . See Louis (1988), Stanek et al. (1989) Term 4, 2006 BIO 656 --Multilevel Models 18

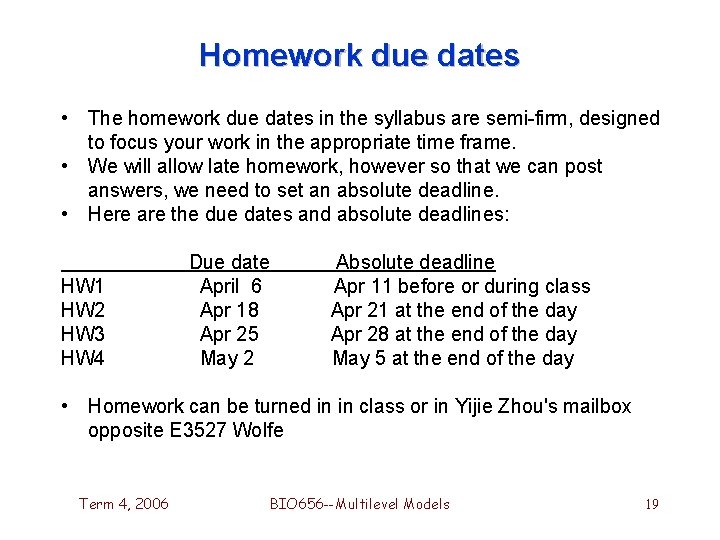
Homework due dates • The homework due dates in the syllabus are semi-firm, designed to focus your work in the appropriate time frame. • We will allow late homework, however so that we can post answers, we need to set an absolute deadline. • Here are the due dates and absolute deadlines: HW 1 HW 2 HW 3 HW 4 Due date April 6 Apr 18 Apr 25 May 2 Absolute deadline Apr 11 before or during class Apr 21 at the end of the day Apr 28 at the end of the day May 5 at the end of the day • Homework can be turned in in class or in Yijie Zhou's mailbox opposite E 3527 Wolfe Term 4, 2006 BIO 656 --Multilevel Models 19

Random Effects Models • Latent effects are unobserved – inferred from the correlation among residuals • Random effects models prescribe the marginal mean and the source of correlation • Assumptions about the latent variables determine the nature of the correlation matrix Term 4, 2006 BIO 656 --Multilevel Models 20

Conditional and Marginal Models Conditioning on random effects • For linear models, regression coefficients and their interpretation in conditional & marginal models are identical: average of linear model = linear model of average • For non-linear models, coefficients have different meanings and values - Marginal models: - population-average parameters - Conditional models: - Cluster-specific parameters Term 4, 2006 BIO 656 --Multilevel Models 21

Term 4, 2006 BIO 656 --Multilevel Models 22

Term 4, 2006 BIO 656 --Multilevel Models 23

Term 4, 2006 BIO 656 --Multilevel Models 24

Term 4, 2006 BIO 656 --Multilevel Models 25

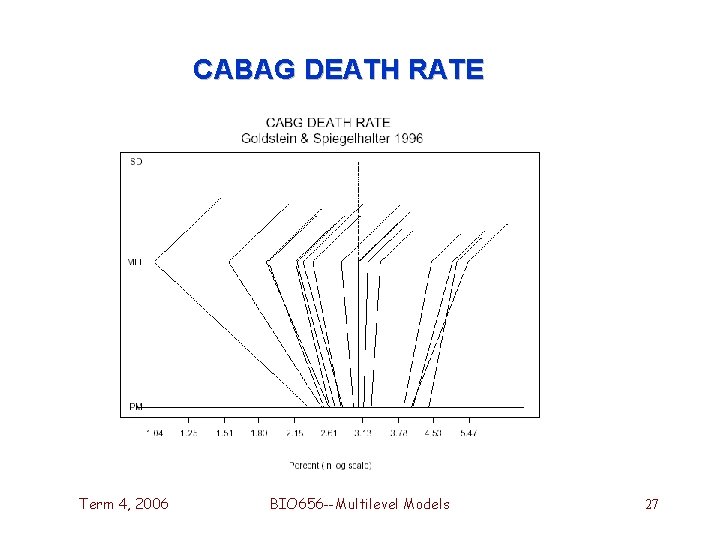
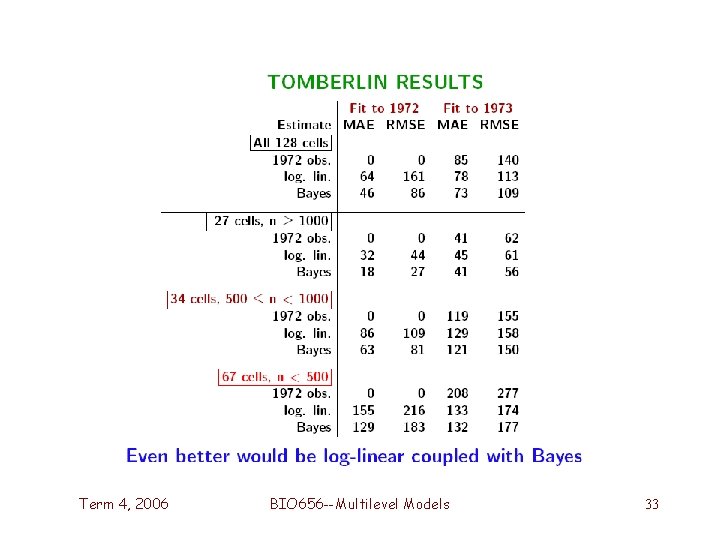
Death Rates for Coronary Artery Bypass Graft (CABG) Term 4, 2006 BIO 656 --Multilevel Models 26

CABAG DEATH RATE Term 4, 2006 BIO 656 --Multilevel Models 27

Term 4, 2006 BIO 656 --Multilevel Models 28

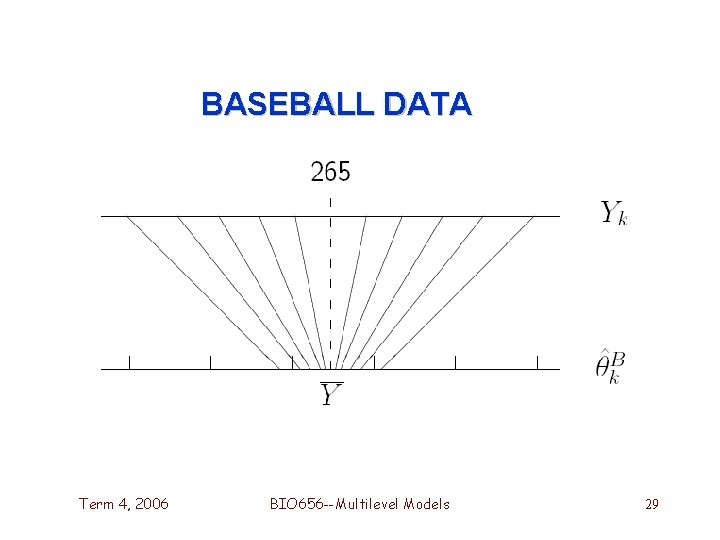
BASEBALL DATA Term 4, 2006 BIO 656 --Multilevel Models 29

Term 4, 2006 BIO 656 --Multilevel Models 30

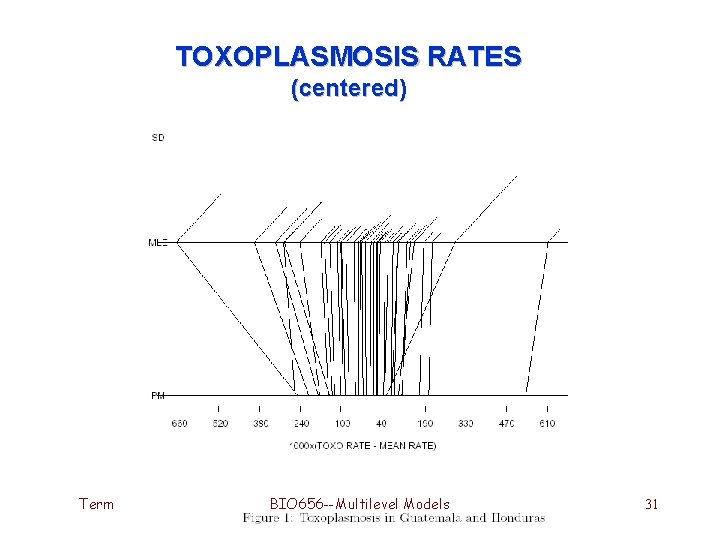
TOXOPLASMOSIS RATES (centered) Term 4, 2006 BIO 656 --Multilevel Models 31

Term 4, 2006 BIO 656 --Multilevel Models 32

Term 4, 2006 BIO 656 --Multilevel Models 33

Deviation, Specialists’ Charges Observed & Predicted Deviations of Annual Charges (in dollars) for Specialist Services vs. Primary Care Services John Robinson’s research Dot (red) = Posterior Mean of Observed Deviation Term 4, 2006 Square (blue) = Posterior Mean of Predicted Deviation BIO 656 --Multilevel Models 34

Mean Deviation of Log(Charges >$0) Observed and Predicted Deviations for Specialist Services: Log(Charges>$0) and Probability of Any Use of Service John Robinson’s research Dot (red) = Posterior Mean of Observed Deviation Square (blue) = Posterior Mean of Predicted Deviation Term 4, 2006 BIO 656 --Multilevel Models 35

Informal Information Borrowing Term 4, 2006 BIO 656 --Multilevel Models 36

Term 4, 2006 BIO 656 --Multilevel Models 37

Term 4, 2006 BIO 656 --Multilevel Models 38

Term 4, 2006 BIO 656 --Multilevel Models 39

DIRECT ESTIMATES Term 4, 2006 BIO 656 --Multilevel Models 40

A Linear Mixed Model Term 4, 2006 BIO 656 --Multilevel Models 41

Term 4, 2006 BIO 656 --Multilevel Models 42

Term 4, 2006 BIO 656 --Multilevel Models 43

Term 4, 2006 BIO 656 --Multilevel Models 44

Effect of Regressors at Various Levels • Including regressors at a level will reduce the size of the variance component at that level • And, reduce the sum of the variance components • Including may change “percent accounted for” but sometimes in unpredictable ways • Except in the perfectly balanced case, including regressors will also affect other variance components Term 4, 2006 BIO 656 --Multilevel Models 45

“Vanilla” Multi-level Model (for Patients Physicians Clinics) • i indexes patient, j physician, k clinic • Yijk = measured value for ith patient, jth physician in the kth clinic Pure vanilla Yijk = + ai + bj + ck • With no replications at the patient level, there is no residual error term Total Variance Term 4, 2006 BIO 656 --Multilevel Models 46

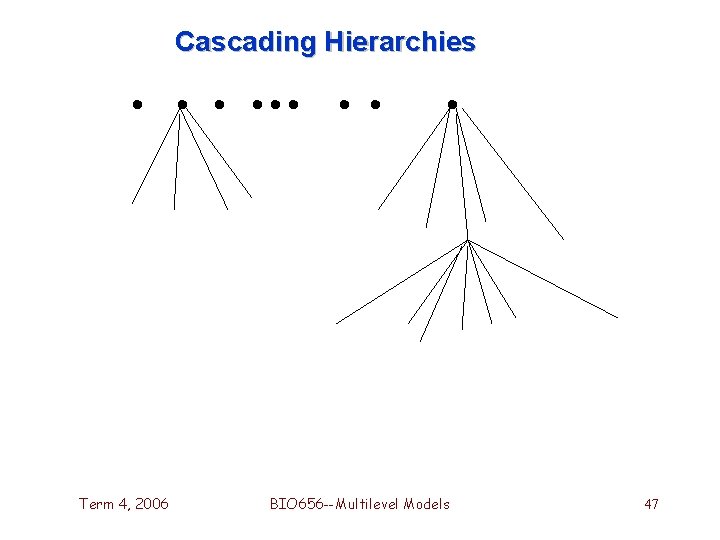
Cascading Hierarchies Term 4, 2006 BIO 656 --Multilevel Models 47

With a physician-level covariate • Xjk is a physician level covariate • This is equivalent to using the full subscript Xijk but noting that Xijk = Xi jk for all i and i Model with a covariate Yijk = + ai + bj + ck + Xjk • Compute the total variance and percent accounted for as before, but now there is less overall variability, less at the physician level and, usually, a reallocation of the remaining variance Term 4, 2006 BIO 656 --Multilevel Models 48

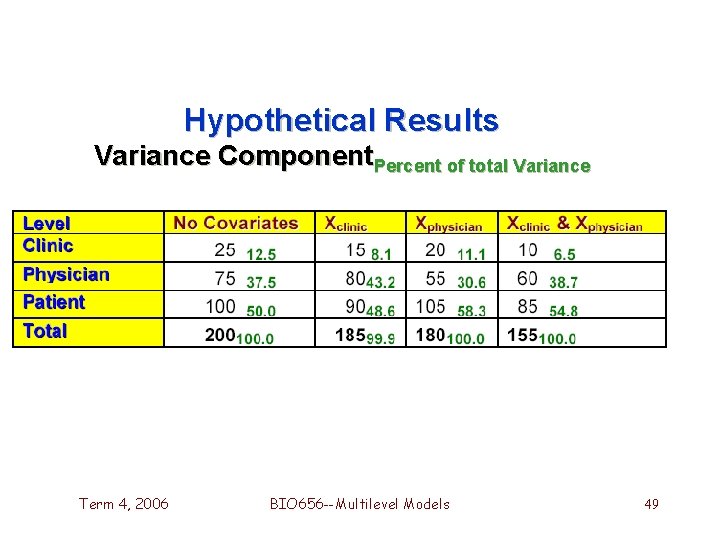
Hypothetical Results Variance Component. Percent of total Variance Term 4, 2006 BIO 656 --Multilevel Models 49

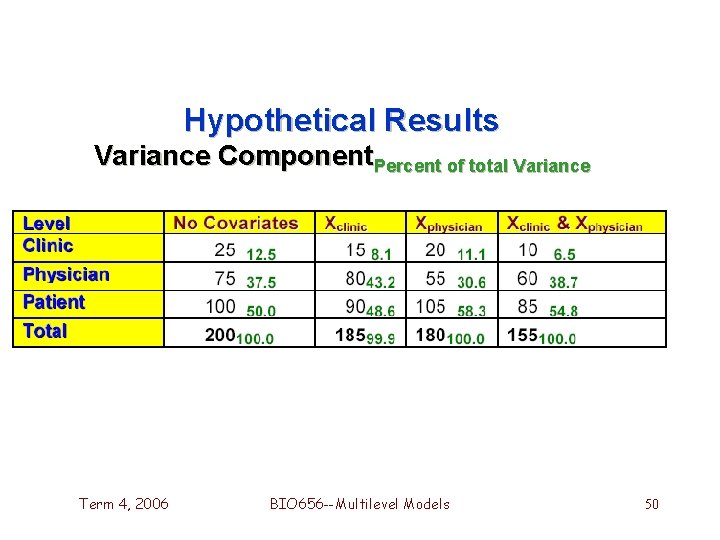
Hypothetical Results Variance Component. Percent of total Variance Term 4, 2006 BIO 656 --Multilevel Models 50

Term 4, 2006 BIO 656 --Multilevel Models 51

Term 4, 2006 BIO 656 --Multilevel Models 52

Term 4, 2006 BIO 656 --Multilevel Models 53

Random Effects should replace “unit of analysis” • Models contain Fixed-effects, Random effects (Variance Components) and other correlationinducers • There are many “units” and so in effect no single set of units • Random Effects induce unexplained (co)variance • Some of the unexplained may be explicable by including additional covariates • MLMs are one way to induce a structure and estimate the REs Term 4, 2006 BIO 656 --Multilevel Models 54