Part 2 Basics Marianne Winslett 1 4 Xiaokui

Part 2: Basics Marianne Winslett 1, 4, Xiaokui Xiao 2, Gerome Miklau 3, Yin Yang 4, Zhenjie Zhang 4, 1 University of Illinois at Urbana Champaign, USA 2 Nanyang Technological University, Singapore 3 University of Massachusetts Amherst, USA 4 Advanced Digital Sciences Center, Singapore

Agenda �Basics: Xiaokui �Query Processing (Part 1): Gerome �Query Processing (Part 2): Yin �Data Mining and Machine Learning: Zhenjie

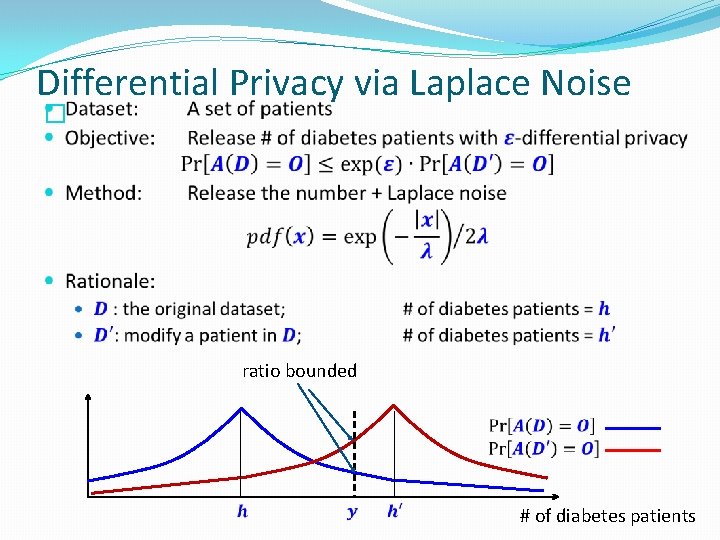
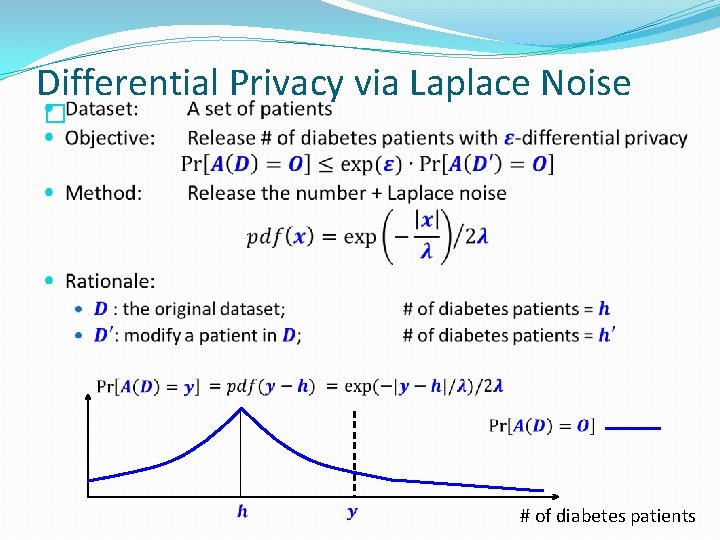
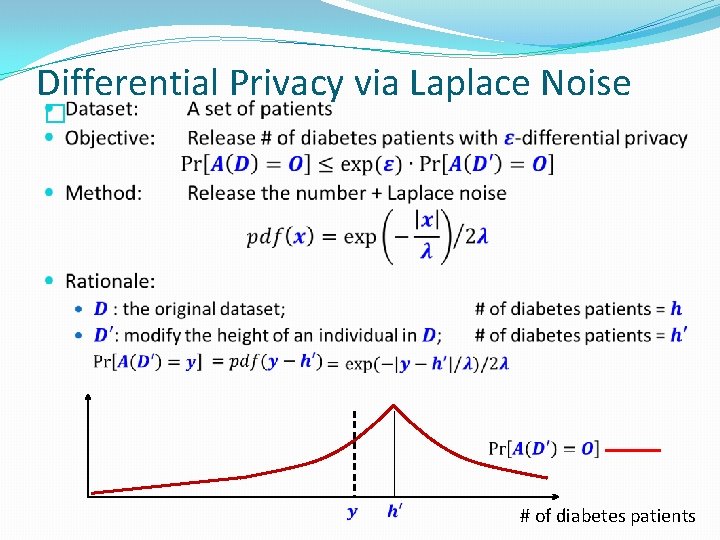
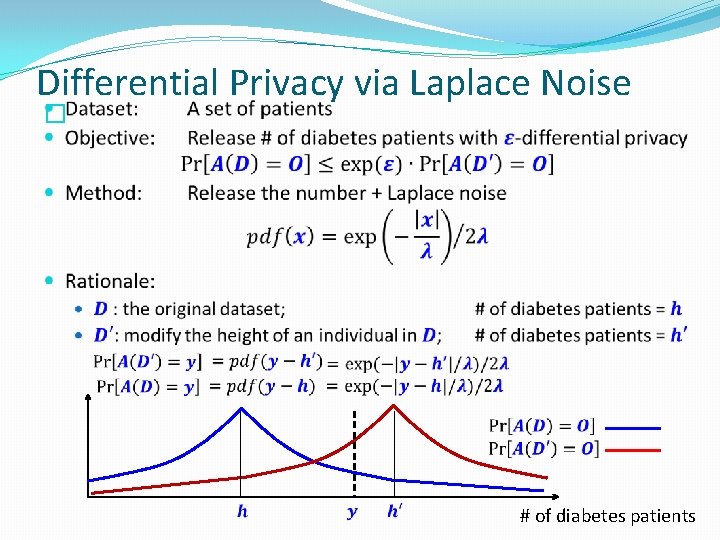
Formulation of Privacy �What information can be published? �Average height of US people �Height of an individual �Intuition: �If something is insensitive to the change of any individual tuple, then it should not be considered private �Example: �Assume that we arbitrarily change the height of an individual in the US �The average height of US people would remain roughly the same �i. e. , The average height reveals little information about the exact height of any particular individual


� ratio

� 100% # of diabetes patients
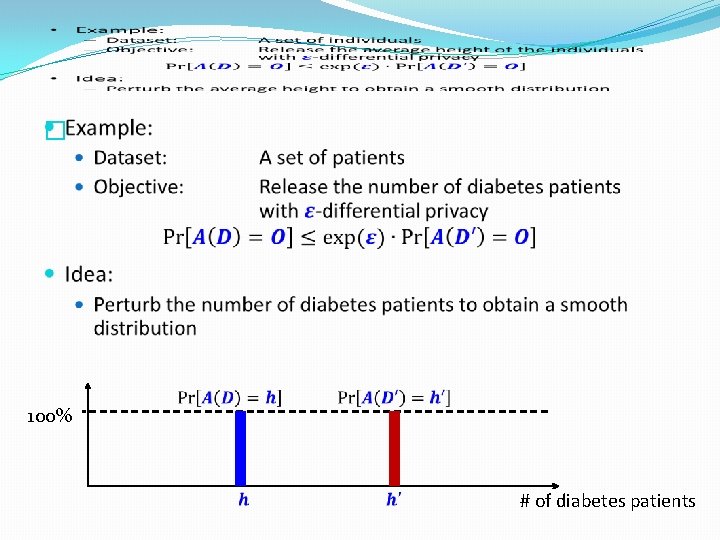
� 100% # of diabetes patients
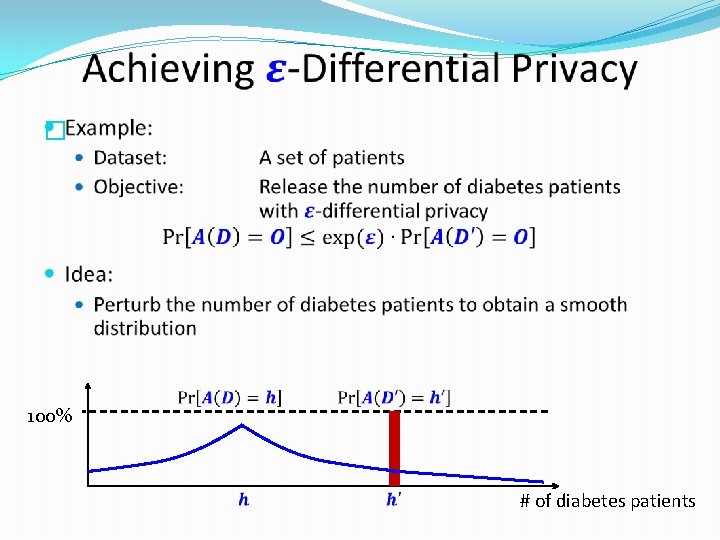
� 100% # of diabetes patients
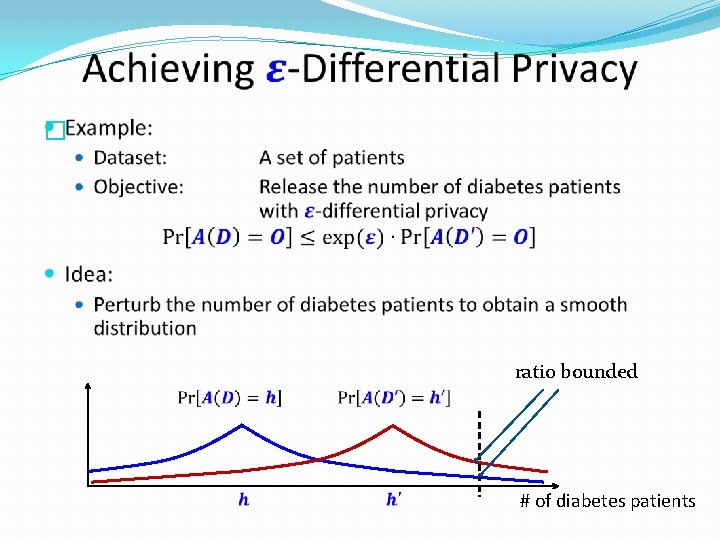
� ratio bounded # of diabetes patients
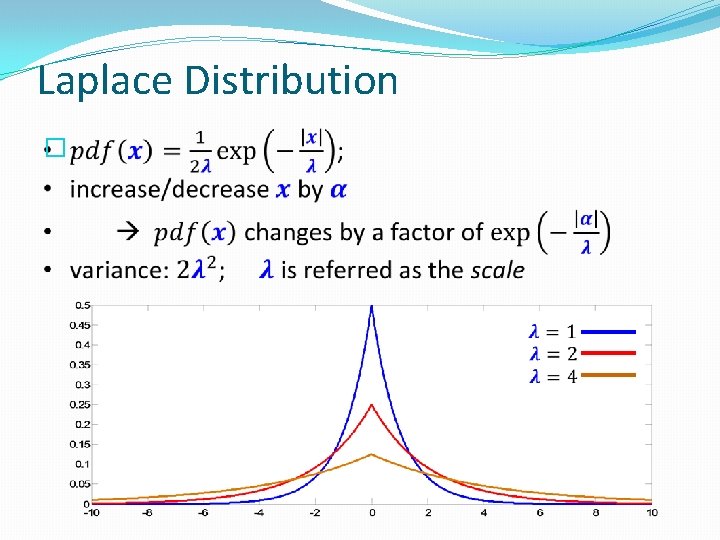
Laplace Distribution �
Differential Privacy via Laplace Noise � ratio bounded # of diabetes patients
Differential Privacy via Laplace Noise � # of diabetes patients
Differential Privacy via Laplace Noise � # of diabetes patients
Differential Privacy via Laplace Noise � # of diabetes patients
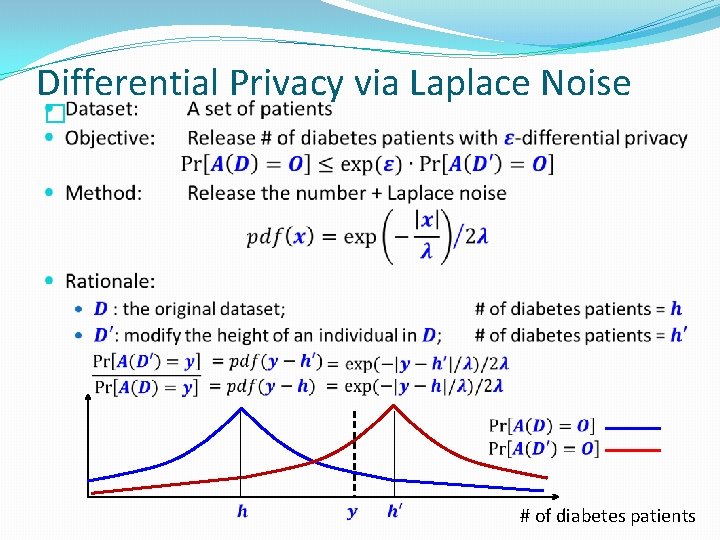
Differential Privacy via Laplace Noise � # of diabetes patients
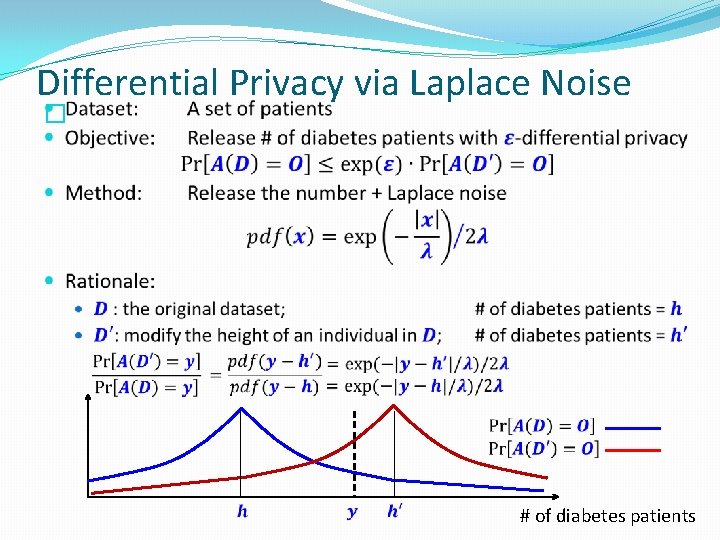
Differential Privacy via Laplace Noise � # of diabetes patients
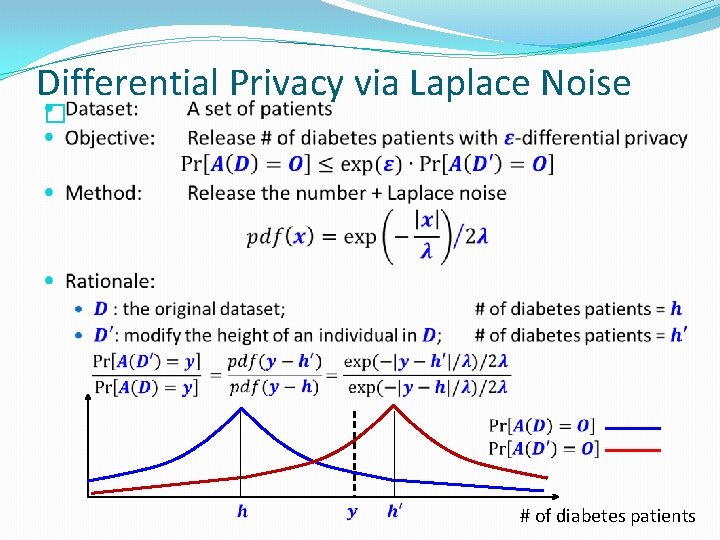
Differential Privacy via Laplace Noise � # of diabetes patients
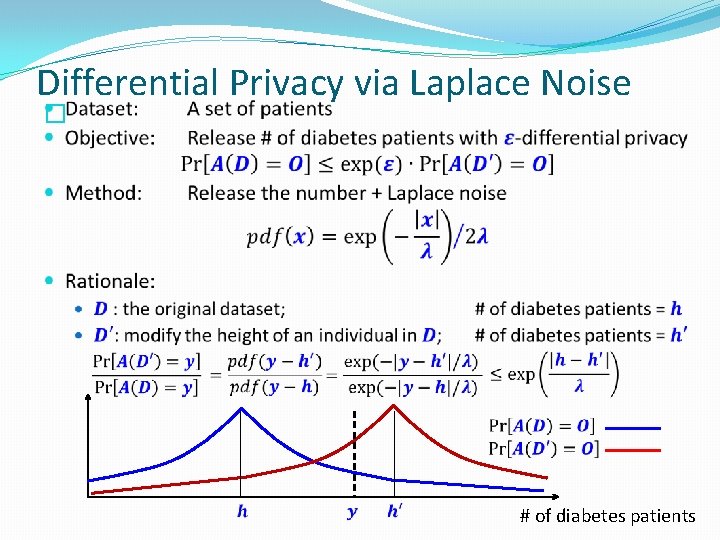
Differential Privacy via Laplace Noise � # of diabetes patients
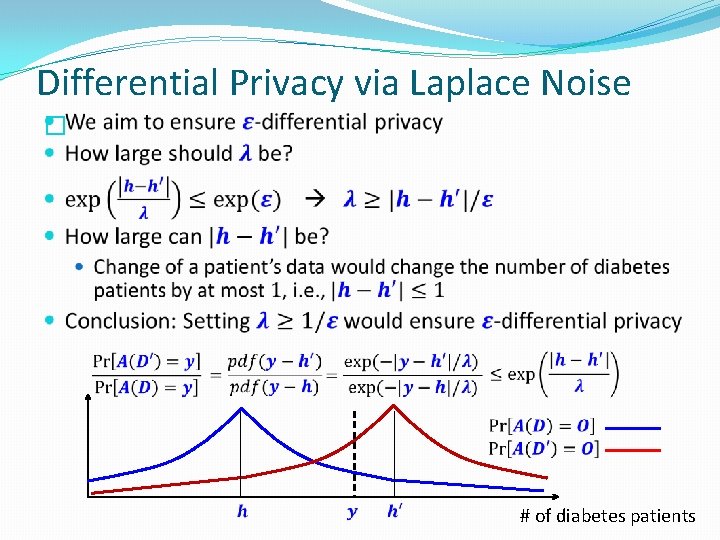
Differential Privacy via Laplace Noise � # of diabetes patients

Differential Privacy via Laplace Noise �

Differential Privacy via Laplace Noise �

Sensitivity of Queries �
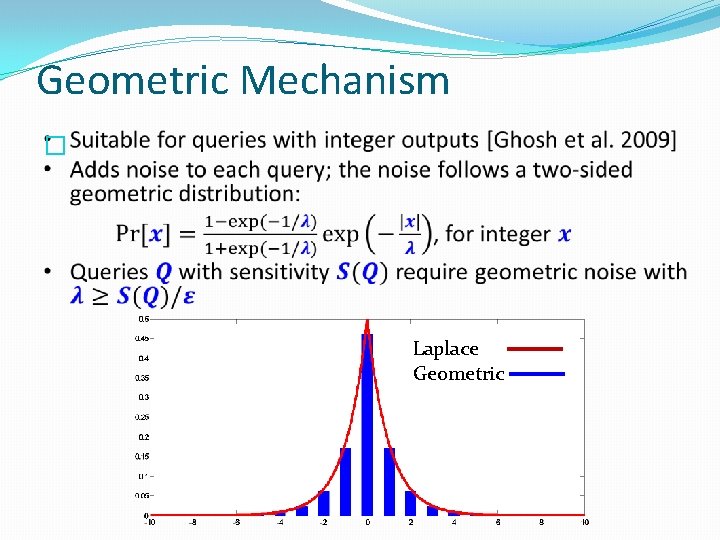
Geometric Mechanism � Laplace Geometric

Exponential Mechanism �

Exponential Mechanism (cont. ) �

Exponential Mechanism (cont. ) �

Composition of Differential Privacy �

Variants of Differential Privacy �

Variants of Differential Privacy �

Variants of Differential Privacy �

Variants of Differential Privacy �

Limitations of Differential Privacy �Differential privacy tends to be less effective when there exist correlations among the tuples �Example (from [Kifer and Machanavajjhala 2011]): �Bob’s family includes 10 people, and all of them are in a database �There is a highly contagious disease, such that if one family member contracts the disease, then the whole family will be infected �Differential privacy would underestimate the risk of disclosure �Summary: Amount of noise needed depends on the correlations among the tuples, which is not captured by differential privacy
- Slides: 32