Part 1 Stability Analysis of Linear Switched Systems

Part 1 Stability Analysis of Linear Switched Systems: An Optimal Control Approach Michael Margaliot School of Elec. Eng. Tel Aviv University, Israel Joint work with: Gideon Langholz (TAU), Daniel Liberzon (UIUC), Michael S. Branicky (CWRU), Joao Hespanha (UCSB). 1

Overview l l l Switched systems Global asymptotic stability The edge of stability Stability analysis: q An optimal control approach q A geometric approach q An integrated approach Conclusions 2
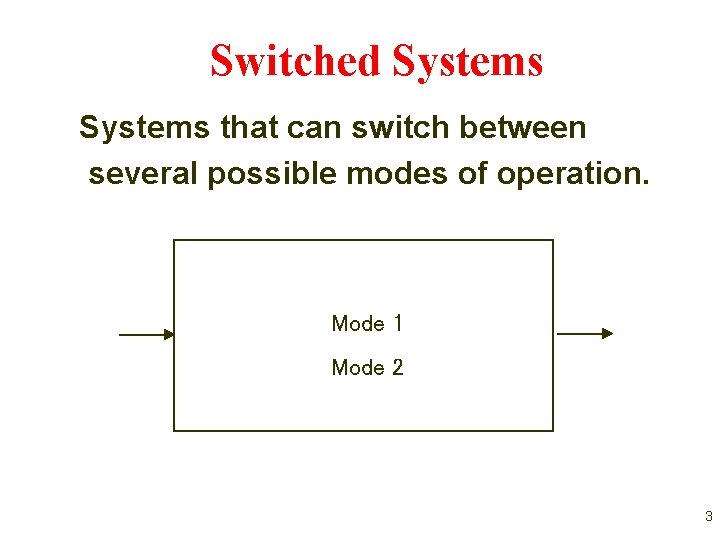
Switched Systems that can switch between several possible modes of operation. Mode 1 Mode 2 3
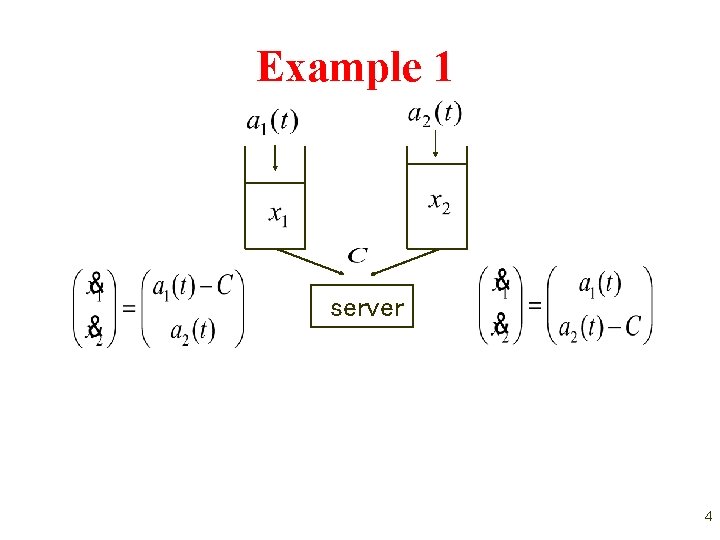
Example 1 server 4
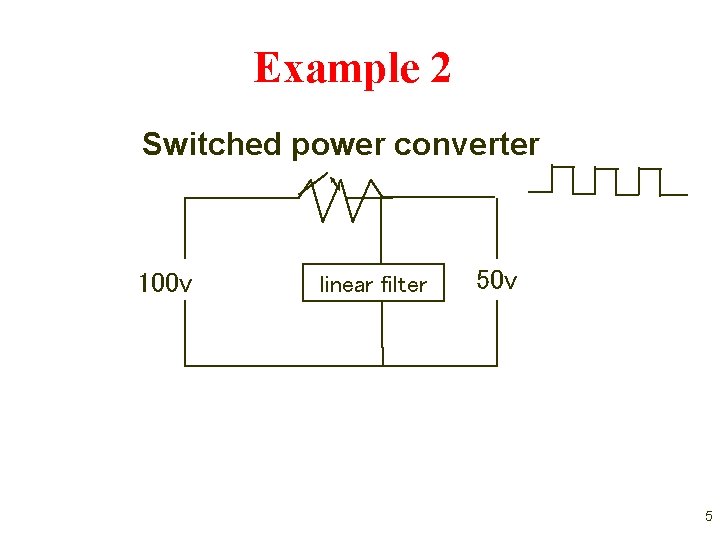
Example 2 Switched power converter 100 v linear filter 50 v 5
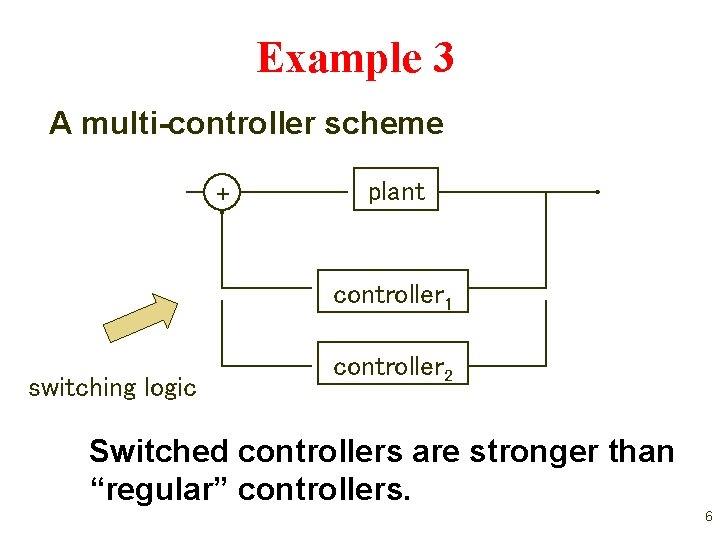
Example 3 A multi-controller scheme + plant controller 1 switching logic controller 2 Switched controllers are stronger than “regular” controllers. 6

More Examples l Air traffic control l Biological switches l Turbo-decoding l …… 7

Synthesis of Switched Systems Driving: use mode 1 (wheels) Braking: use mode 2 (legs) The advantage: no compromise 8

Linear Systems Solution: Definition: The system is globally asymptotically stable if Theorem: stability A is called a Hurwitz matrix. 9

Linear Switched Systems Two (or more) linear systems: A system that can switch between them: 10 10

Stability Linear switched system: Definition: Globally uniformly asymptotically stable (GUAS): In other words, for any AKA, “stability under arbitrary switching”. 11 11

A Necessary Condition for GUAS The switching law yields Thus, a necessary condition for GUAS is that both are Hurwitz. Then instability can only arise due to repeated switching. 12 12

Why is the GUAS problem difficult? Answer 1: The number of possible switching laws is huge. 13 13
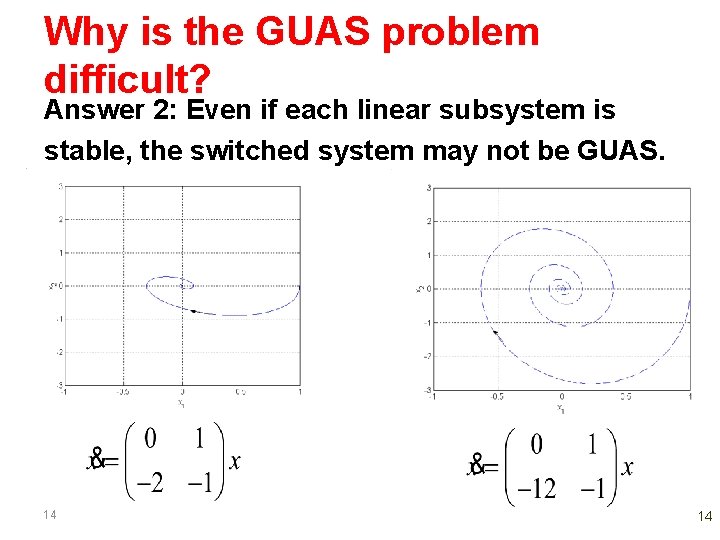
Why is the GUAS problem difficult? Answer 2: Even if each linear subsystem is stable, the switched system may not be GUAS. 14 14
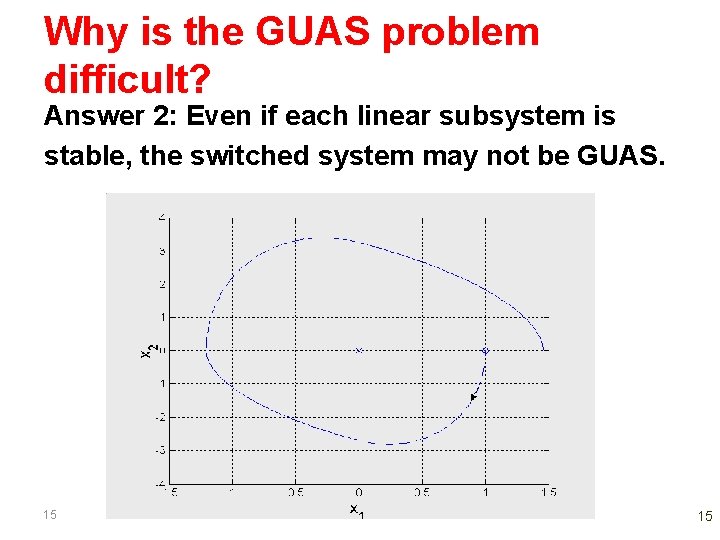
Why is the GUAS problem difficult? Answer 2: Even if each linear subsystem is stable, the switched system may not be GUAS. 15 15
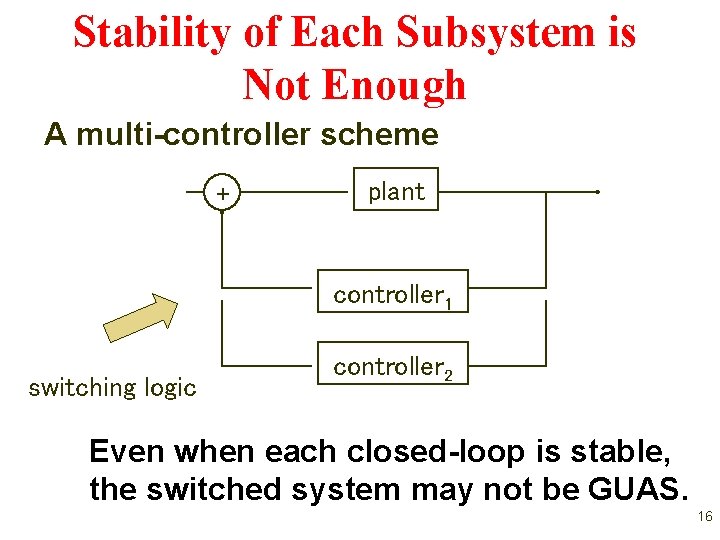
Stability of Each Subsystem is Not Enough A multi-controller scheme + plant controller 1 switching logic controller 2 Even when each closed-loop is stable, the switched system may not be GUAS. 16

Easy Case #1 A trajectory of the switched system: Suppose that the matrices commute: Then and since both matrices are Hurwitz, the switched system is GUAS. 17 17

Easy Case #2 Suppose that both matrices are upper triangular: Then Now so so This proves GUAS. 18 18

Optimal Control Approach Pioneered by E. S. Pyatnitsky (1970 s). Basic idea: (1) A relaxation: linear switched system → bilinear control system (2) characterize the “most destabilizing” control (3) the switched system is GUAS iff 19 19

Optimal Control Approach Relaxation: the switched system: → a bilinear control system: where is the set of measurable functions taking values in [0, 1]. 20

Optimal Control Approach The bilinear control system (BCS) is globally asymptotically stable (GAS) if: Theorem The BCS is GAS if and only if the linear switched system is GUAS. 21

Optimal Control Approach The most destabilizing control: Fix a final time . Let Optimal control problem: find a control that maximizes Intuition: maximize the distance to the origin. 22

Optimal Control Approach and Stability Theorem The BCS is GAS iff 23
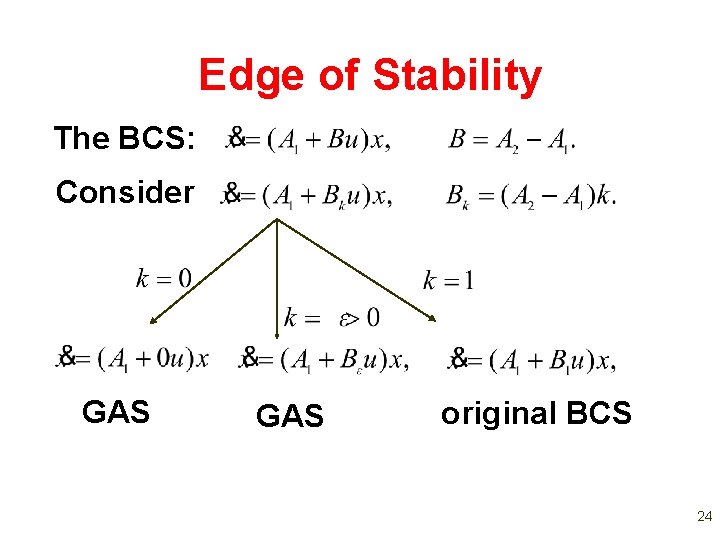
Edge of Stability The BCS: Consider GAS original BCS 24
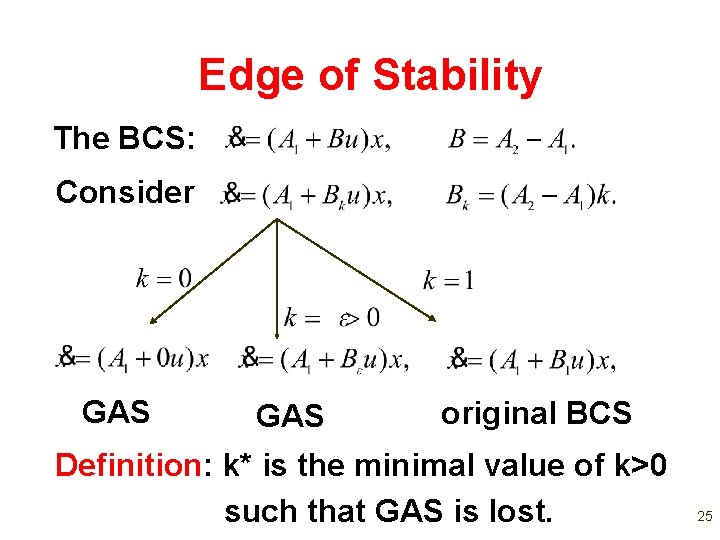
Edge of Stability The BCS: Consider GAS original BCS Definition: k* is the minimal value of k>0 such that GAS is lost. 25

Edge of Stability The BCS: Consider Definition: k* is the minimal value of k>0 such that GAS is lost. The system the edge of stability. is said to be on 26

Edge of Stability The BCS: Consider Definition: k* is the minimal value of k>0 such that GAS is lost. 0 k* 1 k 0 1 k* k Proposition: our original BCS is GAS iff k*>1. 27

Edge of Stability The BCS: Consider Proposition: our original BCS is GAS iff k*>1. → we can always reduce the problem of analyzing GUAS to the problem of determining the edge of stability. 28
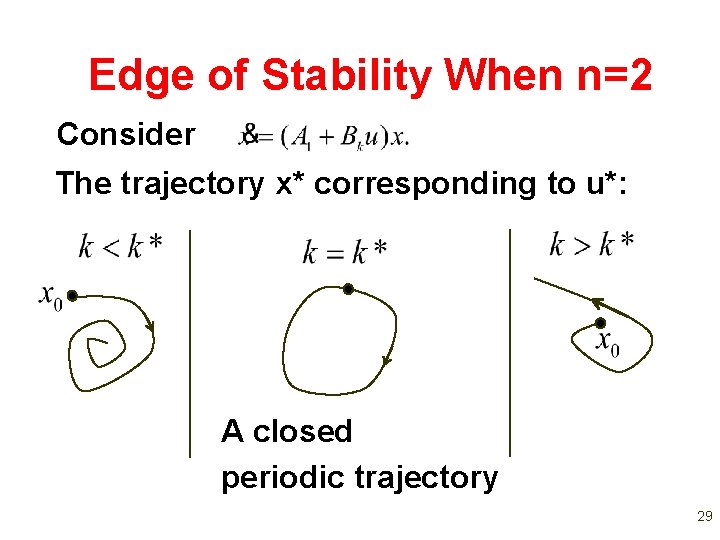
Edge of Stability When n=2 Consider The trajectory x* corresponding to u*: A closed periodic trajectory 29

Solving Optimal Control Problems is a functional: Two approaches: 1. The Hamilton-Jacobi-Bellman (HJB) equation. 2. The Maximum Principle. 30

Solving Optimal Control Problems 1. The HJB equation. Intuition: there exists a function and V can only decrease on any other trajectory of the system. 31

The HJB Equation Find such that Integrating: or An upper bound for , obtained for the maximizing (HJB). 32

The HJB for a BCS: Hence, In general, finding Note: u* depends on is difficult. only. 33

The Maximum Principle Let Differentiating Then, we get A differential equation for boundary condition at with a 34

Summarizing, The WCSL is the maximizing that is, We can simulate the optimal solution backwards in time. 35

Result #1 (Margaliot & Langholz, 2003) An explicit solution for the HJB equation, when n=2, and {A, B} is on the “edge of stability”. This yields an easily verifiable necessary and sufficient condition for stability of second-order switched linear systems. 36

Basic Idea The HJB eq. is: Thus, Let be a first integral of that is, Then is a concatenation of two first integrals and 37
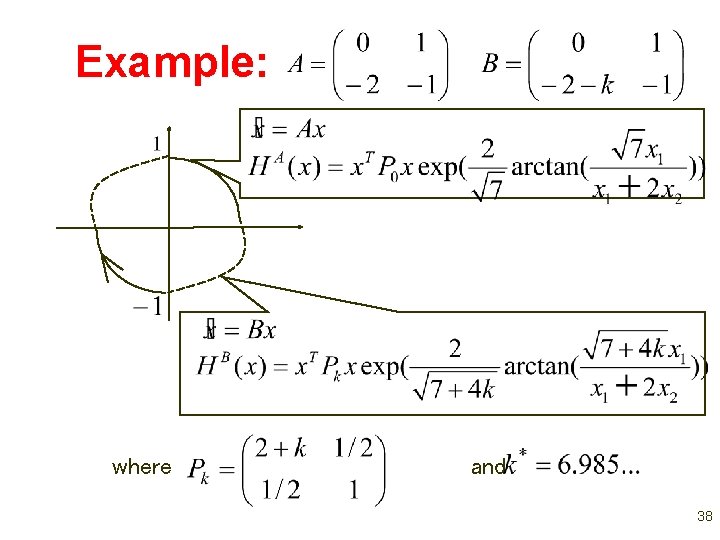
Example: where and 38

Nonlinear Switched Systems with GAS. Problem: Find a sufficient condition guaranteeing GAS of (NLDI). 39

Lie-Algebraic Approach For the sake of simplicity, we present the approach for LDIs, that is, and 40

Commutation and GAS Suppose that A and B commute, AB=BA, then Definition: The Lie bracket of Ax and Bx is [Ax, Bx]: =ABx-BAx. Hence, [Ax, Bx]=0 implies GAS. 41

Lie Brackets and Geometry Consider A calculation yields: 42
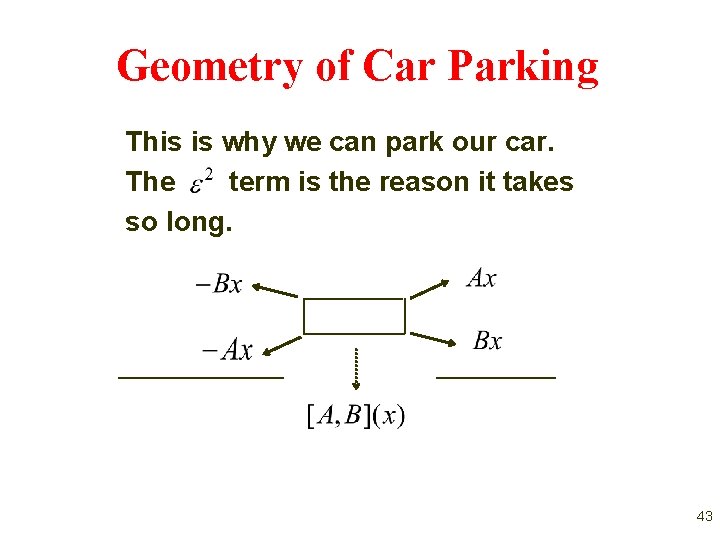
Geometry of Car Parking This is why we can park our car. The term is the reason it takes so long. 43
![Nilpotency We saw that [A, B]=0 implies GAS. What if [A, B]]=[B, [A, B]]=0? Nilpotency We saw that [A, B]=0 implies GAS. What if [A, B]]=[B, [A, B]]=0?](http://slidetodoc.com/presentation_image_h/c02e9ff62b1f4ada4449d3cc92df0592/image-44.jpg)
Nilpotency We saw that [A, B]=0 implies GAS. What if [A, B]]=[B, [A, B]]=0? Definition: k’th order nilpotency all Lie brackets involving k terms vanish. [A, B]=0 → 1 st order nil. [A, B]]=[B, [A, B]]=0 → 2 nd order nil. 44

Nilpotency and Stability We saw that 1 st order nilpotency Implies GAS. A natural question: Does k’th order nilpotency imply GAS? 45

Some Known Results Switched linear systems: l k=2 implies GAS (Gurvits, 1995). l k order nilpotency implies GAS (Liberzon, Hespanha, and Morse, 1999). (The proof is based on Lie’s Theorem) Switched nonlinear systems: l k=1 implies GAS. l An open problem: higher orders of k? (Liberzon, 2003) 46

A Partial Answer Result #2 (Margaliot & Liberzon, 2004) 3 rd order nilpotency implies GAS. Proof: Consider the WCSL Define the switching function 47

Differentiating m(t) yields 2 nd order nilpotency no switching in the WCSL! Differentiating again, we get 3 rd order nilpotency up to a single switching in the WCSL. 48

Singular Arcs If m(t) 0, then the Maximum Principle provides no direct information. Singularity can be ruled out using the auxiliary system. 49

Summary l Parking cars is an underpaid job. l Switched systems and differential inclusions are important in various scientific fields, and pose interesting theoretical questions. l Stability analysis is difficult. A natural and useful idea is to consider the worst-case trajectory. 50

Summary: Optimal Control Approach Advantages: reduction to a single control leads to necessary and sufficient conditions for GUAS allows the application of powerful tools (high-order MPs, HJB equation, Liealgebraic ideas, …. ) applicable to nonlinear switched systems Disadvantages: requires characterizing explicit results for particular cases only 51

More Information 1. Margaliot. “Stability analysis of switched systems using variational principles: an introduction”, Automatica, 42: 2059 -2077, 2006. 2. Sharon & Margaliot. “Third-order nilpotency, nice reachability and asymptotic stability”, J. Diff. Eqns. , 233: 136 -150, 2007. 3. Margaliot & Branicky. “Nice reachability for planar bilinear control systems with applications to planar linear switched systems”, IEEE Trans. Automatic Control, 54: 1430 -1435, 2009. Available online: 52 www. eng. tau. ac. il/~michaelm 52
- Slides: 52