Part 1 Ordinary Differential Equations Ch 1 FirstOrder











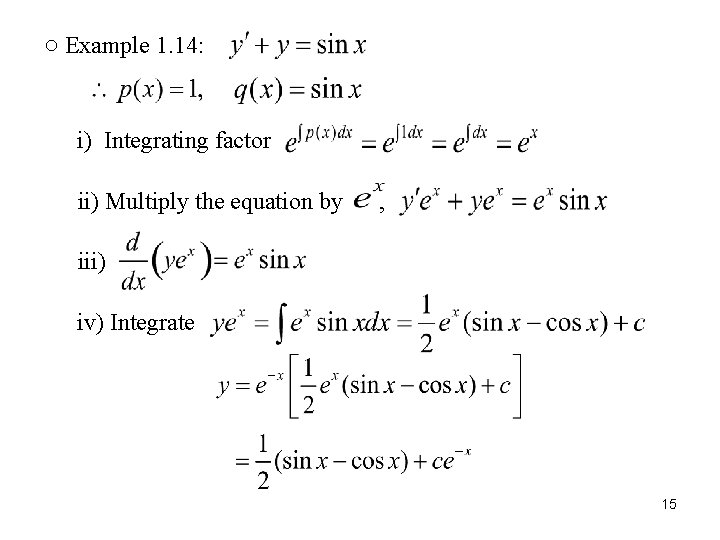

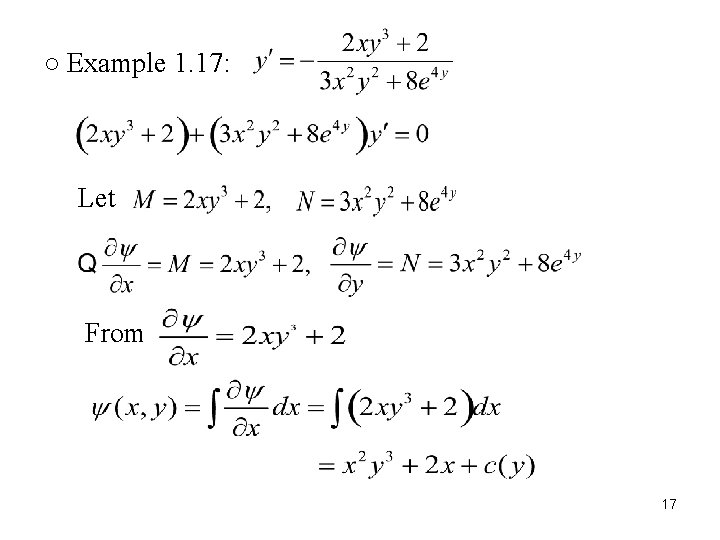



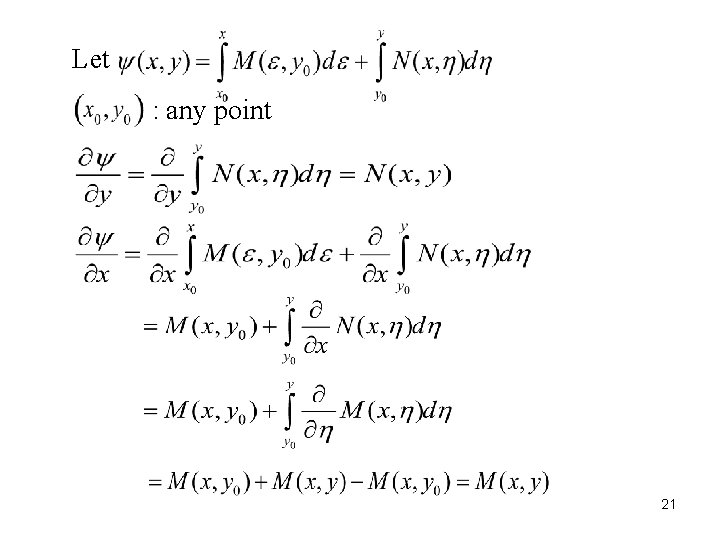






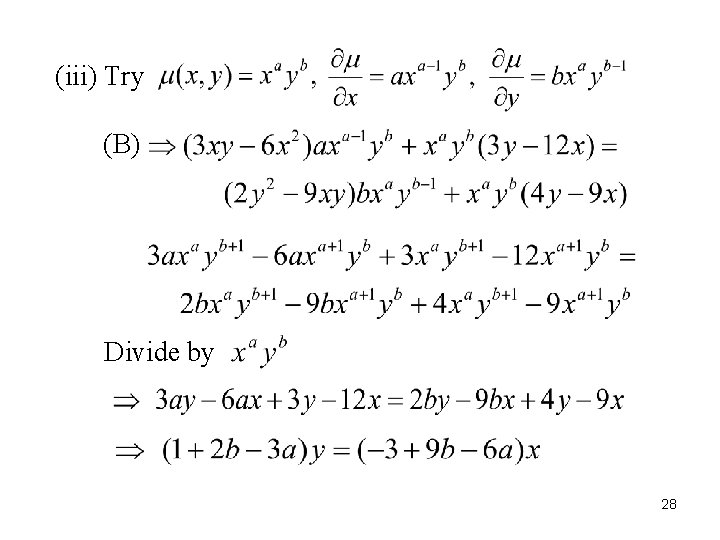



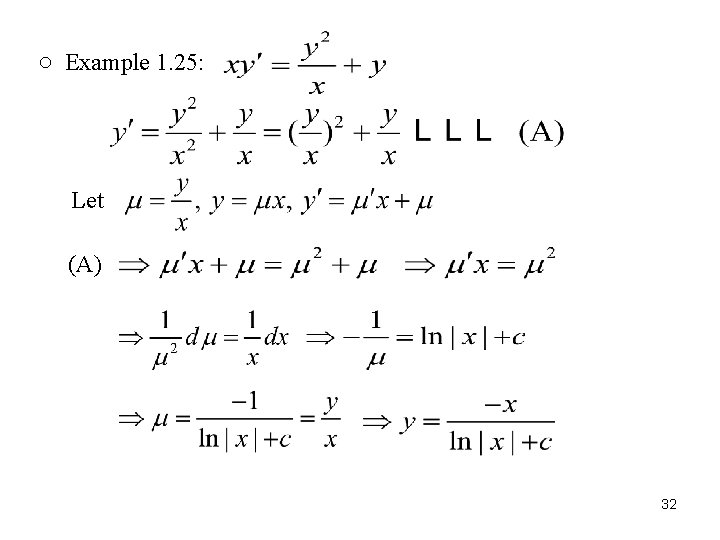













- Slides: 45

Part 1: Ordinary Differential Equations Ch 1: First-Order Differential Equations Ch 2: Second-Order Differential Equations Ch 3: The Laplace Transform Ch 4: Series Solutions 1

(a) Differential equation --- contains derivatives e. g. , or or y : function of x, x : independent variable (b) Ordinary differential equation – involves only total derivatives Partial differential equation – involves partial derivatives What is 2

(c) The order of a differential equation e. g. , ○ The solution of a differential equation is a function y(x) of independent variable x that may be defined on e. g. , i) ii) , solution: y = sin 2 x for , solution: y = xlnx – x for x > 0 3

Ch. 1: First-Order Differential Equations 1. 1. Preliminary Concepts ○ First-order differential equation: -- involves a first but no higher derivatives e. g. , y:function of x x:independent variable : solution 4

1. 1. 1. General and Particular Solutions ○ General solution: arbitrary constant Substitute into (A) Particular solutions: k = 1, k= ; k=2, , 5

1. 1. 2. Implicitly Defined Solutions ○ Explicit function: Implicit function: e. g. , , ○ (Explicit solution) (Implicit solution) 6

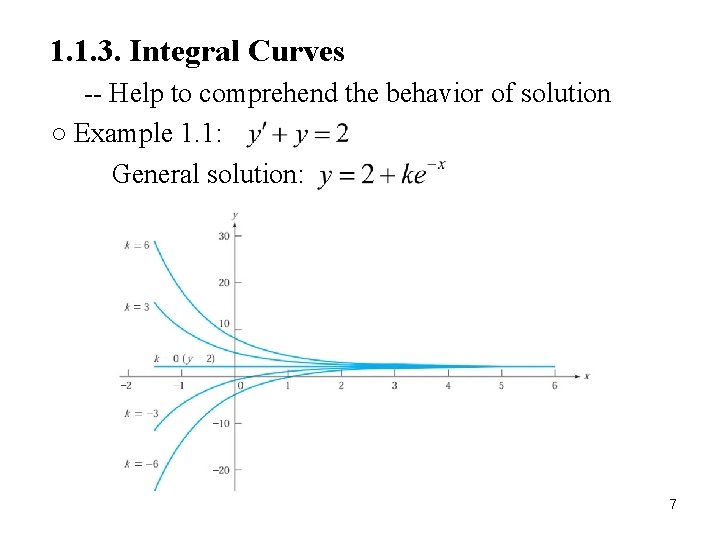
1. 1. 3. Integral Curves -- Help to comprehend the behavior of solution ○ Example 1. 1: General solution: 7

1. 1. 4. Initial Value Problems ○ initial condition Graphically, the particular integral curve passes through point ( ) The objective is to obtain a unique solution ○ Example 1. 4: , initial condition General solution: , 8

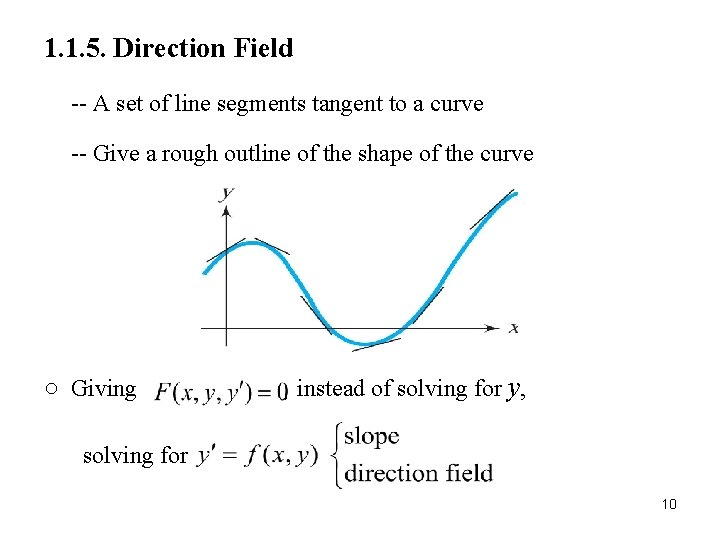
1. 1. 5. Direction Field -- A set of line segments tangent to a curve -- Give a rough outline of the shape of the curve ○ Giving , instead of solving for y, solving for 9

1. 1. 5. Direction Field -- A set of line segments tangent to a curve -- Give a rough outline of the shape of the curve ○ Giving , instead of solving for y, solving for 10

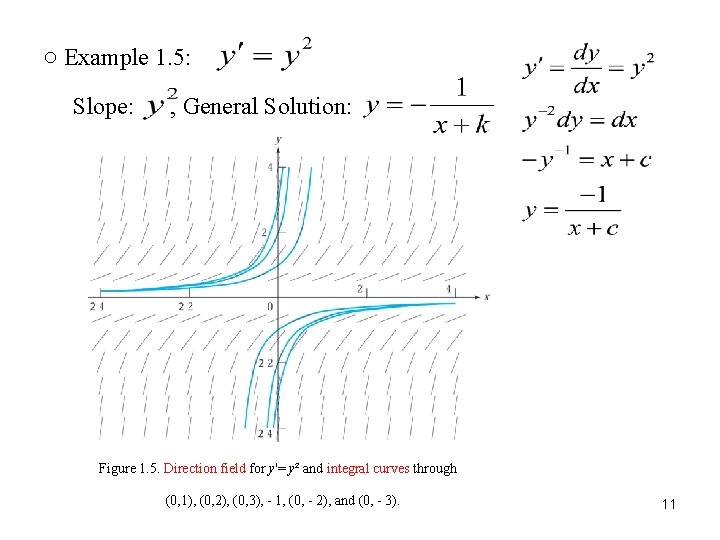
○ Example 1. 5: Slope: , General Solution: Figure 1. 5. Direction field for y'= y² and integral curves through (0, 1), (0, 2), (0, 3), - 1, (0, - 2), and (0, - 3). 11

1. 2. Separable Equations 12

○ Example 1. 7: , (the general solution) y = 0 is a solution, called a singular solution, it cannot be obtained from the general solution 13

1. 3. Linear Differential Equations ---- (A) (1) Find integrating factor: (2) Multiply (A) by (3) 14
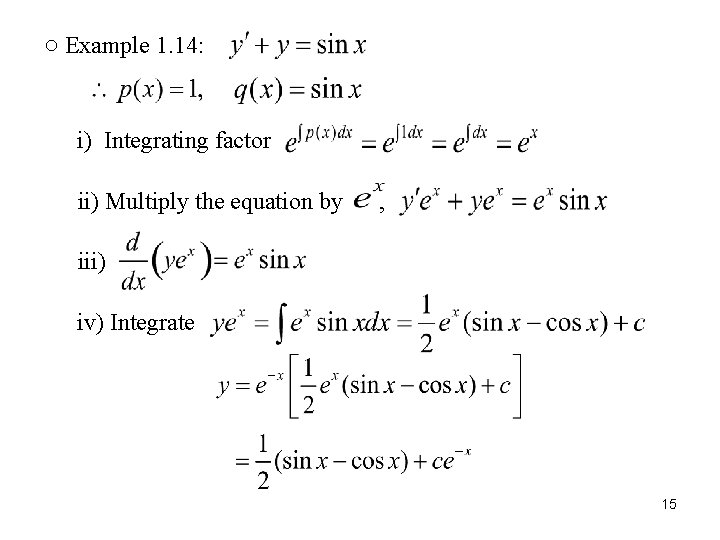
○ Example 1. 14: i) Integrating factor ii) Multiply the equation by , iii) iv) Integrate 15

1. 4. Exact Differential Equations can be written as ------- (A) If , s. t. and (implicitly define the solution) : potential function 16
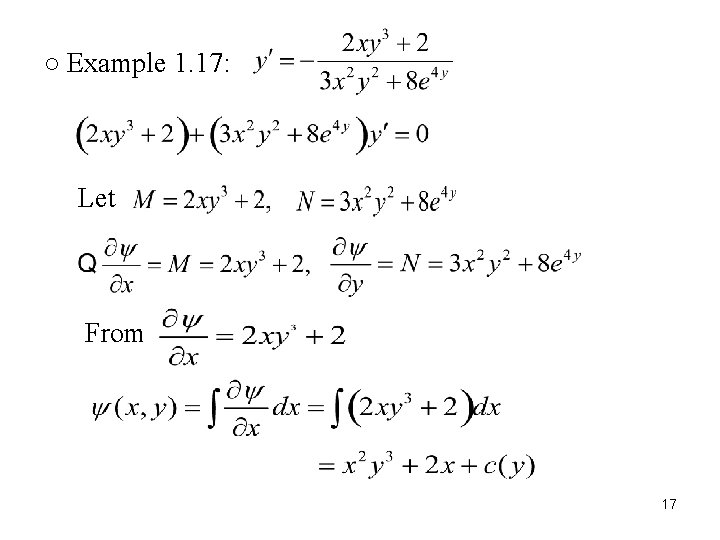
○ Example 1. 17: Let From 17

From Solution: * We can start with , then as well 18

* Not every is exact e. g. From c(y) is not independent of x No potential function 19

Theorem 1. 1: Exactness is exact iff (a) If then (b) If is exact, s. t. , show s. t. 20
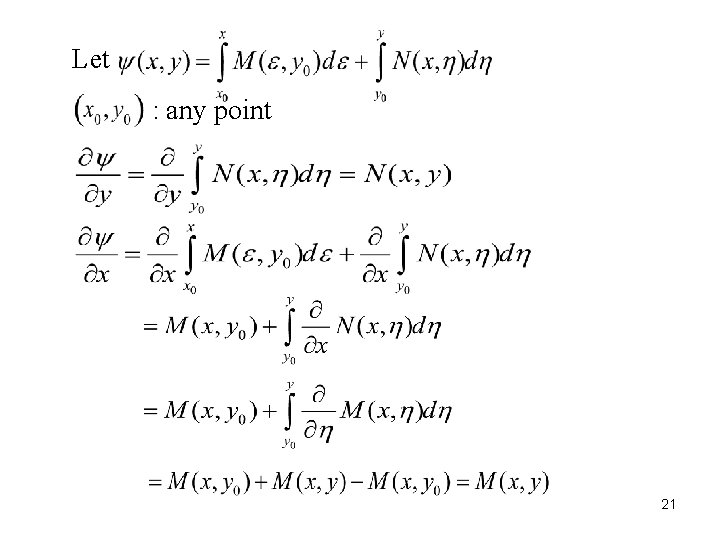
Let : any point 21

○ Example : is not exact 1. 5. Integrating Factors If But : not exact : exact integrating factor 22

○ How to find : exact, Try as , or ○ Example 1. 21: . The equation is not exact 23

Consider Let Try (B) Integrate 24

(A) Let be the potential function The implicit solution: The explicit solution: 25

○ Example 1. 22: Let Find integrating factor by 26

(i) Try This cannot be solved for as a function of x (ii) Likewise, let 27
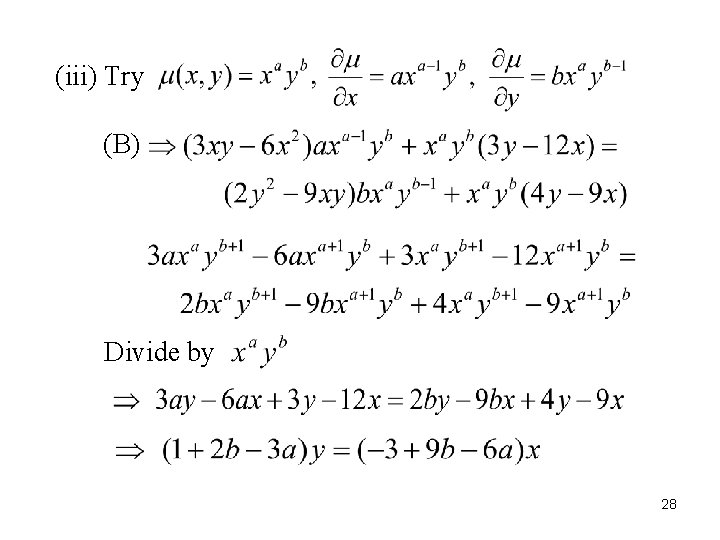
(iii) Try (B) Divide by 28

: independent Multiply (A) by Let Form 29

From Obtain the potential function The implicit solution: or 30

1. 6. Homogeneous, Bernoulli, and Riccati Eqs. 1. 6. 1 Homogeneous Equation: ----- (A) * A homogeneous equation is always transformed into a separable one by letting ↑=1 (A) 31
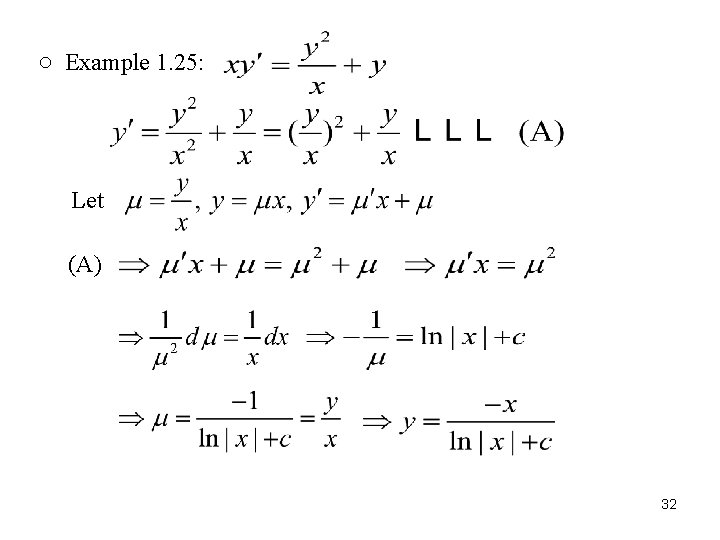
○ Example 1. 25: Let (A) 32

1. 6. 2. Bernoulli Equation linear separable can be transformed into linear by 33

○ Example 1. 27: Let (A) Multiply by (linear) Integrating factor: 34

1. 6. 3. Riccati Equation Let S(x) be a solution and let The Riccati equation is transformed into linear ○ Example 1. 28: By inspection, is a solution of (A) Let 35

(linear) Integrating factor: Integrate and Solution: 36

1. 8. Existence and Uniqueness for Solutions of Initial Value Problems: The problem may have no solution and may have multiple solutions ○ Example 1. 30: The equation is separable and has solution The equation has no real solution. is not a solution because it does not satisfy the initial condition. 37

○ Example 1. 31: The equation has solution This problem has multiple solutions i, Trivial solution: ii, Define Consider All satisfy the initial condition 38

○ Theorem 1. 2: If f, then : continuous in , s. t. The initial value problem has a unique solution defined on The size of h depends on f and 39

○ Example 1. 31: not continuous on (x, 0) ○ Example:The problem : both continuous on the entire plane and hence on s. t. the problem has a unique solution in Solve the problem for , we can take , which is valid 40

○ Theorem 1. 3: : continuous on I The problem , has a unique solution defined Proof: From the general solution of the linear equation and the initial condition , the solution of the initial value problem is : continuous on I, the solution is defined 41

Homework 1 Chapter 1 Sec. 1. 1: Sec. 1. 2: Sec. 1. 3: Sec. 1. 4: Sec. 1. 5: 1, 2, 7, 12 1, 2, 11 1 42

1. 5(1): Determine a test involving M and N to tell when has an integrating factor that is a function of y only. Ans: Let be an integrating factor such that is exact. Then, 43

The test is then that must be independent of x. 44

Homework 2 Chapter 1 Sec. 1. 6: 15, 16, 20, 21 Sec. 1. 8: 1, 3, 5 45