Part 1 Introduction to Graphviz NEATO DOT Synopsis

Part 1: Introduction to Graphviz

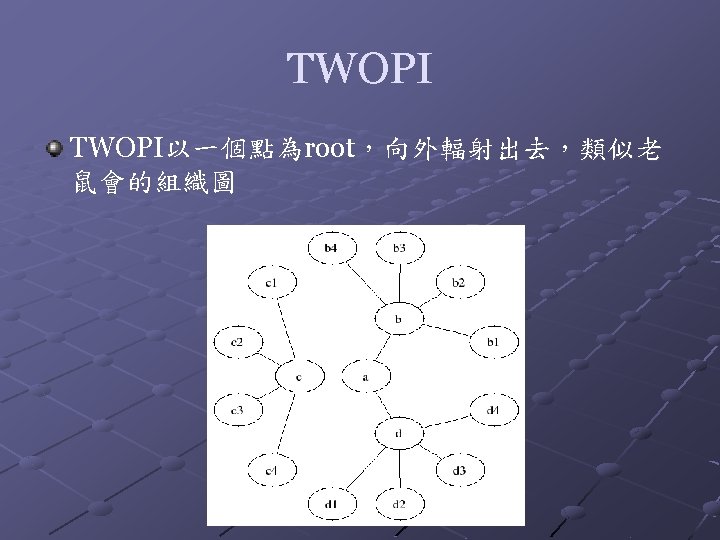
NEATO

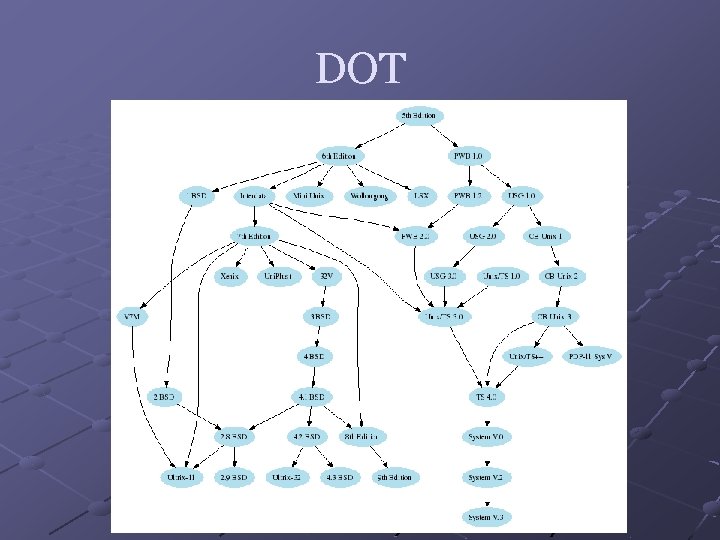
DOT

Synopsis Neato -Ttype -n -o output files n n type: 輸出的圖形類別，可為png、ps、gif、 svg、imap(HTML的imagemap) output: 輸出檔的檔名 files: 要處理的Graphviz檔 -n: 強制用絕對座標 Ex: neato -Tpng -o a. png a. dot

Syntax (1/3) Graphviz中的物件分為四類：graph、 subgraph、node、edge，只有graph是最 上層物件，其他三個都要放在graph中 創造新的graph物件 n graph_name { statement… } 創造新的node物件 n node_name; 創造新的edge物件(node會自動產生) n n node 1 -- node 2; node 1 -> node 2; (undirected) (directed)

Syntax (2/3) 為graph或subgraph設定屬性 n graph name { name 1 = value 1; name 2 = value 2; } 為node設定屬性 n n 0 [name 0=value 0, name 1=value 1, …]; 為edge設定屬性 n n 0 -- n 1 [name 0=v 0, name 1=v 1, …];

Syntax (3/3) Node的基本屬性 n node [n 1=v 1, n 2=v 2, …]; Edge的基本屬性 n edge [n 1=v 1, n 2=v 2, …]; 色彩的表示法 n n color = “#rrggbb” color = “red”

Example (1/4) graph G 1 { bgcolor="#003333"; node [shape=box, style=filled, fontsize=18, fontname=Vera. BI, fillcolor="#778899”]; a -- b -- c -- a; } Bgcolor Shape Style Fillcolor a -- b -- c -- a

Example (2/4) graph G 1 { node [shape=house, style=bold, fontname=Vera. BI, fillcolor="#778899"]; a -- b -- c -- a; } Style = bold Shape = house

Example (3/4) graph G 1 { node [shape=house, style=bold, fontname=Vera. BI, fillcolor="#778899"]; a [label="Hello, n. World!", fontsize=22, shape=polygon, sides=7, regular=0. 5]; } Label Shape = polygon Sides = 7 Regular = 0. 5

Example (4/4) graph G 1 { node [shape=box, style=filled, fontname=Vera. BI, fillcolor="#778899"]; edge [fontname=Vera. BI, fontcolor="#AABB 88", dir=forward]; a [label="Regularn. Expression"]; b [label="dfa or nfa"]; c [label="Regularn. Grammar"]; a -- b [label="theorem 3. 1", len=2, arrowhead=dot, arrowsize=10]; b -- c [label="theorem 3. 4", len=3]; } Define nodes and edges Len Arrowhead, arrowtail, arrowsize Dir = forward (back, both, none)

Node Attributes label = “the text on the node” fontsize, fontname, fontcolor = “the color of the border” fillcolor = “the color of inner area” fontcolor = “the color of the text” style = the style of the border URL = “the url in imagemap” Pos = “x, y”

Edge Attributes len = the length of the edge label fontsize, fontname, fontcolor dir = {forward, back, both, none} arrowhead, arrowtail, arrowsize headlabel, taillabel color

Part 2: c-Means Clustering Algorithm

Problem Description (1/3) Let O={o 1, o 2, …, on} be a set of n objects. We want to partition O into c clusters {C 1, … , Cc} and Ci has ni elements. Let Si is average pairwise dissimilarity of Ci. The criterion of this problem is the sum of ni*Si We don’t know how to determine c, but we try to find a good solution for given c.

Problem Description (2/3) There are two kinds of data. One is object data and the other is relational data. Assume an object has s attributes. Then we can use n s-variate vectors {x 1, …, xn} to represent O. We say xi are object data. Sometimes we don’t know object data, but we know the relational data between each objects. Rij is the dissimilarity of oi and oj. We say R is relational data.

Problem Description (3/3) Properties for any dissimilarity matrix R: n n n Rjk ≥ 0 Rjk = Rkj Rjj = 0 There also two kinds of cluster methods, fuzzy and hard. In hard clustering, one object belongs to just one cluster. In fuzzy clustering, one object belongs to many clusters.

Previous Works Ball and Hall (1967) -- ISODATA n A clustering technique for summarizing multivariate data Goldberg (1989) -- GA n Genetic algorithms in search, optimization and machine learning Ismail (1989) – directed search strategy n Multidimensional data clustering utilizing hybrid search strategies Bezdek and Hathaway (1994) -- GA n Optimization of Fuzzy Clustering Criteria using Genetic Algorithms

This paper Hathaway and Bezdek and Devenport n n On relational data versions of c-means algorithms Pattern Recognition Letters Volume 17 , Issue 6 (May 1996)

Data Representation U is an c x n matrix. U = [U 1 U 2 … Un]. In hard clustering, Ui = ek if oi belongs to cluster k. In fuzzy clustering, the sum of Ui is 1. Because c is fixed, the sum of each row in U is greater than zero.

Criterion Object data Relational data

HCM: Hard c-Means (1/2) 1. Given object data set X = {x 1, …, xn}. Fix c, ε. Initialize U. r = 0 is round. 2. Calculate vi = the center of Ci 3. Calculate dik = the distance between vi and ok Move ok to the cluster with min dik 4. If |U – U’| < εor r > rmax , then stop. Else, continue step 2.

HCM: Hard c-Means (2/2)

RHCM: Relational Hard c-Means (1/3) 目的：找出relational duals of the c-means algorithm 若本來是object data，將 代入RHCM， 能以相同步驟作clustering 若本來是relational data呢? 是否能找到一群 object使 n n R 12 = 1, R 13 = 9, R 23 = 4 Euclidean realization R 12 = 1, R 13 = 16, R 23 = 4

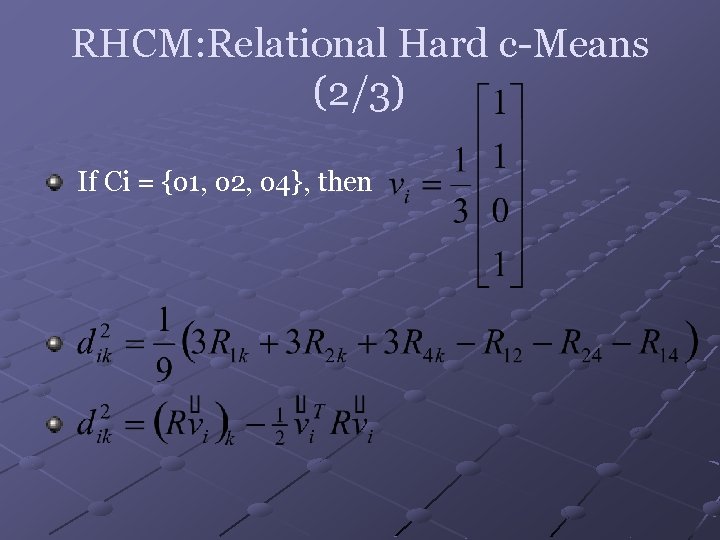
RHCM: Relational Hard c-Means (2/3) If Ci = {o 1, o 2, o 4}, then

RHCM: Relational Hard c-Means (3/3) 1. Given object data set X = {x 1, …, xn}. Fix c, ε. Initialize U. r = 0 is round. 2. Calculate vi. If Ci={o 1, o 2, o 4}, then vi=[1 1 0 1]’/ni 3. Calculate dik = a magic number Move ok to the cluster with min dik 4. If |U – U’| < εor r > rmax , then stop. Else, continue step 2.

NERHCM: non-Euclidean Relational Hard c-Means (1/4) 目的：補足RHCM不足的部分 方法：β-spreading n In R(β), Rij = Rij + β if i≠j Ex: R 12=1, R 23=4, R 13=16 n n n β =2: R 12=3, R 23=6, R 13=18 β =6: R 12=7, R 23=10, R 13=22 β =10: R 12=11, R 23=14, R 13=26

NERHCM: non-Euclidean Relational Hard c-Means (2/4) If (dik)^2 < 0 for some i, k, then Update

NERHCM: non-Euclidean Relational Hard c-Means (3/4) 1. Given object data set X = {x 1, …, xn}. Fix c, ε. Initialize U. r = 0 is round. β= 0. 2. Let R = R(β) Calculate vi. If Ci={o 1, o 2, o 4}, then vi=[1 1 0 1]’/ni 3. Calculate dik = a magic number If dik < 0 for some i and k, update β and dik Move ok to the cluster with min dik 4. If |U – U’| < εor r > rmax , then stop. Else, continue step 2.

NERHCM: non-Euclidean Relational Hard c-Means (4/4) 作者的證明 n n There exists β’ such that for all β> β’, R(β) is Euclidean realization R(β) is rank-order preserving K(R(β), U) = K(R, U) + (β/2)(n-c) There exists b>0 such that for any R(β) with β>b, NERHCM will terminate at round 0 for any U. 結論：relational data 及 object data 的演算法可 以互通

Reference Data Clustering: a review n n n Jain, Murty, and Flynn (1999) ACM Computing Surveys Vol. 31 , Issue 3, 1999 The neighbor-joining method: a new method for reconstructing phylogenetic trees n n n Saitou and Nei Molecular Biology and Evolution Vol. 4, No. 4, 1987