PART 1 Axioms of Probability 1 1 Introduction

PART 1 Axioms of Probability 1. 1 Introduction 1. 2 Sample Space and Events 1. 3 Axioms of Probability 1. 4 Basic Theorems 1. 5 Continuity of Probability Function 1. 6 Probabilities 0 and 1 1. 7 Random Selection of Points from Intervals EE 571 1

1. 1: Introduction Overview: An event may or may not occur q What’s Certain? Occurrence of an event is inevitable q What’s Impossible? An event can never occur Examples: 1. Disintegration of a given atom of radium 2. Finding no defect during inspection of a microwave oven 3. Orbit satellite in space is at a certain position 4. An object travels faster than light 5. A thunderstorm flashes of lighting precede any thunder echoes q What’s Random? EE 571 2

Relative Frequency Interpretation Definition:the probability p of event A is definded as Dilemmas: Can not be computed since n , only approximation 2. Does the limit of n(A)/n exist? 3. Probabilities that are based on our belief and knowledge are not justifiable. The probability that the price of oil will be raised in the next six months is 60%. The probability that it will snow next Christmas is 30% 1. EE 571 3

1. 2: Sample Space and Events q Sample Space: The set of all possible outcomes, denoted by S q Sample points: These outcomes are called sample points, or points. q Events: Certain subsets of S are referred to as events. b f a d e c g k h Sample Space j l i m o n p Sample point Event EE 571 4

Examples q Example 1. 1: For the experiment of tossing a coin once, what is the sample space S ? q Example 1. 2: Suppose that an experiment consists of two steps. First a coin is flipped. If the outcome is tails, a die is tossed. If the outcome is head, the coin is flipped again. What is the sample space S ? What is the event of heads in the first flip of the coin? What is the event of an odd outcome when the die is tossed? EE 571 5

Examples q Example 1. 3: Consider measuring the lifetime of a light bulb. Since any nonnegative real number can be considered as the lifetime of the light bulb (in hours), the sample space S is S = {x:x 0 }. The event E = {x:x 100 } is the event that the light bulb lasts at least 100 hours. The event F = {x:x 1000 } is the event that it lasts at most 1000 hours. The event G = {505. 5} is the event that it lasts exactly 505. 5 hours. EE 571 6

Examples q Example 1. 4: Suppose that a study is being done on all families with one, two, or three children. Let the outcome of the study be the genders of the children in descending order of their ages. What is the sample space S ? What is the event F where the eldest child is a boy? What is the event G where families with exactly 2 girls? Ans:S = { } F={ G={ } } EE 571 7

Examples q Example 1. 5: A bus with a capacity of 34 passengers stops at a station some time between 11: 00 AM and 11: 40 AM every day. What is the sample space of the experiment, consists of counting the number of passengers on the bus and measuring the arrival time of the bus? Ans: What is the event ? Ans: EE 571 8

Examples q Example 1. 6:(Round-off Error) Suppose that each time Jay charges an item to his credit card , he will round the amount to the nearest dollar in his records. Therefore, the round-off error, which is the true value charged minus the amount recorded, is random, with the sample space S={ } The event of rounding off at most 3 cents in a random charge is given by S={ } EE 571 9

Occurrence of an Event q If the outcome of an experiment belongs to an event E, we say that the event E has occurred. If we draw two cards from an ordinary deck of 52 cards and observe that one is a spade and the other a heart, all of the following events have occurred. {sh}, {sh, dd}, {cc, dh, sh}, {hc, sh, ss, hh}, {cc, hh, sh, dd} But none of the events {dh, sc}, {dd}, {cc, hh, ss}, {hd, hc, dc, sd} have occurred. EE 571 10

Relations of Events q Subset An event E is said to be a subset of the event F if, whenever E occurs, F also occurs. E F q Equality Events E and F are said to be equal if the occurrence of E implies the occurrence of F, and vice versa. E=F q Intersection An event is called the intersection of two events E and F if it occurs only whenever E and F occur simultaneously. It is denoted by E F. General Form: EE 571 11

Relations of Events (Cont’d) q Union An event is called the union of events E and F if it occurs whenever at least one of them occurs. It is denoted by E F. General Form: q Complement An event is called the complement of the event E if it only occurs whenever E does not occur, denoted by EC q Difference An event is called the difference of two events E and F if it occurs whenever E occurs but F does not, and is denoted by E F. Notes: EC = S E and E F = E FC EE 571 12

Relations of Events (Cont’d) q Certainty An event is called certain if it its occurrence is inevitable. The sample space is a certain event. q Impossibility An event is called impossibility if there is certainty in its nonoccurence. The empty set is an impossible event. q Mutually Exclusiveness If the joint occurrence of two events E and F is impossible, we say that E and F are mutually exclusive. That is, E F = . EE 571 13
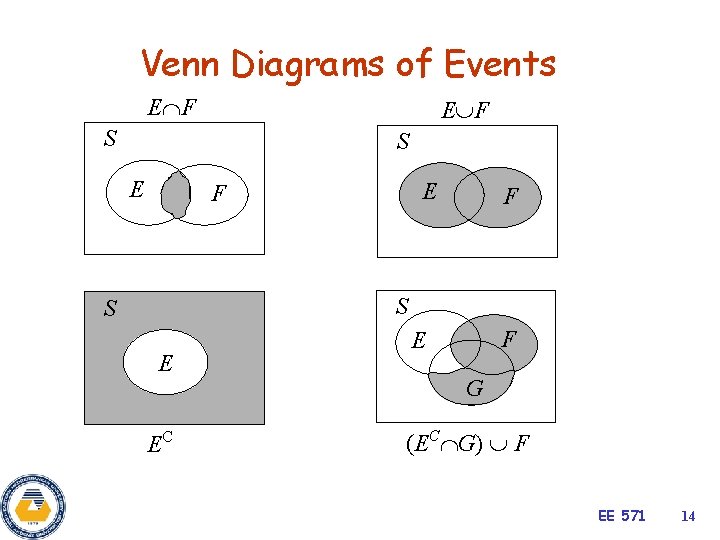
Venn Diagrams of Events E F S S E E F F S S EE EC F F E G (EC G) F EE 571 14

Examples q Example 1. 7 At a busy international airport, arriving planes land on a first-come first-served basis. Let E = there at least 5 planes waiting to land, F = there at most 3 planes waiting to land, H = there are exactly 2 planes waiting to land. Then EC is the event that at most 4 planes are waiting to land. FC is the event that at least 4 planes are waiting to land. E is a subset of FC. That is, E FC = E H is a subset of F. That is, F H = H E and F, E and H are mutually exclusive. F HC is the event that the number of planes waiting to land is 0, 1, or 3. EE 571 15

Useful Laws q Commutative Laws: E F = F E, E F = F E q Associative Laws: E (F G) = (E F) G, E (F G) = (E F) G q Distributive Laws: (E F) H = (E H) (F H), (E F) H = (E H) (F H) q De Morgan’s Laws: (E F)C = EC FC, q De Morgan’s Second Laws: (E F)C = EC FC, EE 571 16

Examples q Example 1. 8 Prove De Morgan’s First Law:For E and F, two events of a sample space S, (E F)C = EC FC = ECFC. Pf: Use Equality property, E = F iff E F and F E. 1. Show that (E F)C EC FC. 2. Show that EC FC (E F)C. EE 571 17

1. 3 Axioms of Probability q Definition: Probability Axioms Let S be the sample space of a random phenomenon. Suppose that to each event A of S, a number denoted by P(A) is associated with A. If P satisfies the following axioms, then it is called a probability and the number P(A) is said to be the probability of A. Axiom 1 Axiom 2 Axiom 3 Equally likely: P(A) = P(B) P(A) 0 P({ 1}) = P({ 2}) P(S) = 1 if {A 1, A 2, A 3, …} is a sequence of mutually exclusive events, then EE 571 18

Theorem 1. 1 The probability of the empty set is 0. That is, P( ) = 0. Pf: EE 571 19

Theorem 1. 2 Let {A 1, A 2, A 3, … , An} be a mutually exclusive set of events. Then Pf: EE 571 20

Properties of Probability q Countable additivity & finite additivity q The probability of the occurrence of an event is always some number between 0 and 1. That is, 0 P(A) 1. q Probability is a real-value, nonnegative, countably additive set function. q The set of all subsets of S is denoted by P(S) and is called the power set of S. EE 571 21

Examples Let P be a probability defined on a sample space S. For events A of S define Q(A) = [P(A)]2 and R(A) = P(A)/2. Is Q a probability on S ? Is R a probability on S ? Why or why not? Sol: EE 571 22

Examples q Example 1. 9 A coin is called unbiased or fair if, whenever it is flipped, the probability of obtaining heads equals that of obtaining tails. When a fair coin is flipped, the sample space is S = {T, H}. Since {H} and {T} are equally likely & mutually exclusive, 1 = P(S) = P({T, H}) = P({T}) + P({H}). Hence, P({T}) = P({H}) = 1/2. When a biased coin is flipped, and the outcome of tails is twice as likely as heads. That is, P({T}) = 2 P({H}). Then 1 = P(S) = P({T, H}) = P({T}) + P({H}) =3 P({H}). Hence, P({H}) = 1/3 and P({T}) = 2/3. EE 571 23

Examples q Example 1. 10 Sharon has baked 5 loaves of bread that are identical except that one of them is underweight. Sharon’s husband chooses one of these loaves at random. Let Bi , 1 i 5, be the event that he chooses the ith loaf. Since all 5 loaves are equally likely to be drawn, we have P(B 1) = P(B 2) = P(B 3) = P(B 4) = P(B 5) Since all {Bi}, 1 i 5, are equally likely & mutually exclusive, 1 = P(S) = P({B 1, B 2 , B 3 , B 4 , B 5 }) = 5 P(B 1). Hence, P(B 1) = 1/5 and P(Bi) = 1/5 , 1 i 5. Therefore, the probability that Sharon’s husband chooses the underweight load is 1/5. EE 571 24

Theorem 1. 3 (Classical Definition of Probability) Let S be the sample space of an experiment. If S has N points that are equally likely to occurs, then for any event A of S, where N(A) is the number of points of A. Pf: EE 571 25

Examples q Example 1. 11 Let S be the sample space of flipping a fair coin three times and A be the event of at least two heads; then S={ } and A = { }. So N = and N(A) =. The probability of event A is. P(A) = N(A)/N =. EE 571 26

Examples q Example 1. 12 An elevator with 2 passengers stops at the second, third, and fourth floors. If it is equally likely that a passenger gets off at any of the 3 floors, what is the probability that the passengers get off at different floors? Sol:Let a and b denote the two passenger and a 2 b 4 mean that a gets off at the 2 nd floor and b gets off at the 4 th floor. So S = { } and A = { }. So N = and N(A) =. The probability of event A is. P(A) = N(A)/N =. EE 571 27

Examples q Example 1. 13 A number is selected at random from the set of integers {1, 2, …, 1000}. What is the probability that the number is divisible by 3? Sol: Let A be the set of all numbers between 1 and 1000 that are divisible by 3. N = 1000, and N(A) = . Hence, the probability of event A is. P(A) = N(A)/N =. EE 571 28

Examples q Example 1. 14 A number is selected at random from the set of integers {1, 2, …, N }. What is the probability that the number is divisible by k, 1 k N ? Sol: Let A be the set of all numbers between 1 and N that are divisible by k. N(A) = N/k . Hence, the probability of event A is. P(A) = N(A)/N = N/k /N. EE 571 29

Remark 1. 3 q Refer to remark 1. 1 Different manifestations of outcomes of an experiment may lead to different representations for the sample space of the same experiment. For example, let the outcomes of the study be the number of girls and the number of boys in a randomly selected family. Then S = {bbb, bgg, bgb, bbg, ggb, gbg, gbb, ggg} and Ω = {bbb, bbg, bgg, ggg} are both reasonable sample space. In S, all sample points occur with probability 1/8. But in Ω, P(bbb) = P(ggg) = 1/8, P(bbg) = P(bgg) = 3/8. EE 571 30

1. 4 Basic Theorem q Theorem 1. 4 S B For any event A, P(AC) = 1 P(A). Pf: A B-A q Theorem 1. 5 If A B, then P(B A) = P( B AC ) = P(B) P(A). Pf: Corollary: If A B, then P(A) P(B). EE 571 31

Theorems q Theorem 1. 6 S A A B B Pf: q Example 1. 15 Suppose that in a community of 400 adults. 300 bike or swim or do both. 160 swim, and 120 swim and bike. What is the probability that an adult, selected at random from this community, bike? Ans: 0. 65 EE 571 32

Examples q Example 1. 16 A number is chosen at random from the set of integers {1, 2, …, 1000}. What is the probability that it is divisible by 3 or 5? Ans: 0. 467. q Example 1. 17 Suppose that 25% of the population of a city read newspaper A, 20% read newspaper B, 13% read C, 10% read both A and B, 8% read both A and C, 5% read B and C, and 4% read all three. If a person from this city is selected at random, what is the probability that he or she does not read any of these newspaper? Ans: 0. 61 EE 571 33

Inclusion-Exclusion Principle q For 3 events q For n events q Theorem 1. 7 EE 571 34

Examples q Example 1. 18 Dr. Grossman, an internist, has 520 patients, of which (1) 230 are hypertensive, (2) 185 are diabetic, (3) 35 are hypochondriac and diabetic, (4) 25 are all three, (5) 150 are none, (6) 140 are only hypertensive, and finally, (7) 15 are hypertensive and hypochondriac but not diabetic. Find the probability that Dr. Grossman’s next appointment is hypochondriac but neither diabetic nor hypertensive. Assume that appointments are all random. This implies that even hypochondriacs do not make more visits than others. Ans: ~0. 06. EE 571 35

Examples q Example 1. 19 In a community, 32% of the population are male smokers; 27% are female smokers. What percentage of the population of this community smoke? Ans: 0. 59. EE 571 36

1. 5 Continuity of Probability Functions q Definition of Continuity For function f:R R, it is called continuous at a point c R if limx c f(x)=f(c). For sequential criterion f:R R, it is continuous on R if and only if, for every convergent sequence in R, q Increasing & Decreasing A sequence {En , n 1} of events of a sample space is called increasing if E 1 E 2 … En …; it is called decreasing if E 1 E 2 … En …. EE 571 37

Continuity of Probability Function q Theorem 1. 8 Pf: EE 571 38

Example 1. 20 Suppose that some individuals in a population produce offspring of the same kind. The offspring of the initial population are called second generation, the offspring of the second generation are called third generation, and so on. If with probability exp[ (2 n 2+7)/(6 n 2)] the entire population completely dies out by the nth generation before producing any offspring, what is the probability that such a population survives forever? Sol: EE 571 39

1. 6 Probabilities 0 and 1 Q:If E and F are events with probabilities 1 and 0, is it correct to say that E is the sample space S and F is the empty set ? Example: Suppose that an experiment consists of selecting a random point from the interval (0, 1), what is the probability that 1/3 is selected ? Sol: Let An be the event that the selected decimal has 3 as its first n digits; then A 1 A 2 A 3 A 4 An An+1 , since the occurrence of An+1 guarantees the occurrence of An. A 1={0. 3, 0. 31. 0. 32, …, 0. 39, 0. 331. 0. 332, …, 0. 339, 0. 3331, …}, A 2={0. 33, 0. 331. 0. 332, …, 0. 339, 0. 3331, …}, … EE 571 40

Example (Cont’d) P(0. 3) = 1/10 = P(A 1) P(0. 33) = 1/100 = P(A 2) P(0. 333) = 1/1000 = P(A 3) … P(An) = 1/10 n Hence, for any point x (0, 1), we have P(x) = 0. So let E = (0, 1) {x}, F = {x}, then P(E) = 1 and P(F) = 0. But E is not the sample space S = (0, 1), and F is not the empty set . EE 571 41

1. 7 Random Selection of Points from Intervals Definition A point is said to be randomly selected from an interval (a, b) if for any two subintervals of (a, b) that have the same length are equally likely to include the point. The probability associated with the event that the subinterval ( , ) contains the point is defined to be ( )/(b a). EE 571 42

EE 571 43

EE 571 44

Chapter 3 Conditional Probability and Independence 3. 1 Conditional Probability 3. 2 Law of Multiplication 3. 3 Law of Total Probability 3. 4 Bayes’ Formula 3. 5 Independence EE 571 45

3. 1 Conditional Probability Definition If P(B) > 0, the conditional probability of A given B, defined by P(A|B), is EE 571 46

Example 3. 1 In a certain region of Russia, the probability that a person lives at least 80 years is 0. 75, and the probability that he or she lives at least 90 years is 0. 63. What is the probability that a randomly selected 80 -year-old person from this region will survive to become 90 ? Sol: Ans: 0. 84 EE 571 47

Example 3. 2 From the set of families with two children, a family is selected at random and is found to have a girl. What is the probability that the other child of the family is a girl? Assume that in a two-child family all sex distributions are equally probable. Sol: Ans: 1/3 EE 571 48

Example 3. 3 From the set of all families with two children, a child is selected at random and is found to be a girl. What is the probability that the second child of this girl’s family is also a girl? Assume that in a two-child family all sex distributions are equally probable. Sol: Ans: 1/2 EE 571 49

Example 3. 4 An English class consists of 10 Koreans, 5 Italians, and 15 Hispanics. A paper is found belonging to one of the students of this class. If the name on the paper is not Korean, what is the probability that it is Italian? Assume that names completely identify ethnic groups. Sol: Ans: 1/4 EE 571 50

Example 3. 5 We draw eight cards at random from an ordinary deck of 52 cards. Given that three of them are spades, what is the probability that the remaining five are also spades? Sol: EE 571 51

Theorem 3. 1 Let S be the sample space of an experiment, and let B be an event of S with P(B) > 0. Then (a) P(A|B) 0 for any event A of S. (b) P(S|B) = 1. (c) If A 1, A 2, …, is a sequence of mutually exclusive events, then Pf: EE 571 52

Reduction of Sample Space The conditional probability P(A|B) over sample space S is equal to the probability P(A’) over the reduced sample space S’ = B. S A A B B S’ EE 571 53

Example 3. 6 A child mixes 10 good and three dead batteries. To find the dead batteries, his father tests them one-by-one and without replacement. If the first four batteries tested are all good, what is the probability that the fifth one is dead? Sol: Ans: 1/3 EE 571 54

Example 3. 7 A farmer decides to test 4 fertilizers for his soybean fields. He buys 32 bags of fertilizers, 8 bags from each kind, and tries them randomly on 32 plots, 8 plots from each of fields A, B, C, and D, one bag per plot. If from type I fertilizer one bag is tried on field A and 3 on field B, what is the probability that two bags of type I fertilizer are tried on field D? Sol: EE 571 55

Example 3. 8 A TV game show, 3 curtains. Behind 2 of 3, there is nothing, but behind the 3 rd there is a prize. The probability that the prize is behind a given curtain is 1/3. The host who knows behind which curtain the prize is, will then pull back a curtain other than the one chosen by the player. The host then give the player the opportunity to change his choice, what will the player do? Sol: EE 571 56

Properties Summary 1. P( |B) = 0 2. P(Ac|B) = 1-P(A|B) 3. If C A, then P(ACc|B) = P(A-C|B) = P(A|B)-P(C|B) 4. If C A, then P(C|B) P(A|B) 5. P(A C|B) = P(A|B) + P(C|B)-P(AC|B) 6. P(A|B) = P(AC|B) + P(ACc|B) 7. P(A 1 A 2 … An|B) =? 8. EE 571 57

3. 2 Law of Multiplication From the definition of conditional probability Then we have Similarly, . . EE 571 58

Example 3. 9 Suppose that 5 good fuses and 2 defective ones have been mixed up. To find the defective fuses, we test them one-by-one, at random and without replacement. What is the probability that we are lucky and find both of the defective fuses in the first two tests? Sol: Ans: 1/21 EE 571 59

Theorem 3. 2 Pf:by Mathematic Induction. (D. I. Y) EE 571 60

Example 3. 10 A consulting firm is awarded 43% of the contracts it bids on. Suppose that Nordulf works for a division of the firm that gets to do 15% of the projects contracted for. If Nordulf directs 35% of the projects submitted to his division, what percentage of all bids submitted by the firm will result in contracts for projects directed by Nordulf? Sol: Ans: 0. 0226 EE 571 61

Example 3. 11 Suppose that 5 good fuses and 2 defective ones have been mixed up. To find the defective fuses, we test them one-by-one, at random and without replacement. What is the probability that we are lucky and find both of the defective fuses in exactly 3 tests? Sol: Ans: 2/21 EE 571 62

3. 3 Law of Total Probability Theorem 3. 3 Let B be an event with P(B) > 0 and P(Bc) > 0. Then for any event A, Pf: EE 571 63

Example 3. 12 An insurance company rents 35% of the cars for its customers from agency I and 65% from agency II. If 8% of the cars of agency I and 5% of the cars of agency II break down during the rental periods, what is the probability that a car rented by this insurance company breaks down? Sol: Ans: 0. 0605 EE 571 64

Example 3. 13 In a trial, the judge is 65% sure that Susan has committed a crime. Julie and Robert are two witness who know whether Susan is innocent or guilty. However, Robert is Susan’s friend and will lie with probability 0. 25 if Susan is guilty. He will tell the truth if she is innocent. Julie is Susan’s enemy and will lie with probability 0. 30 if Susan is innocent. She will tell the truth if Susan is guilty. What is the probability that Robert and Julie will give conflicting testimony? Sol: Ans: 0. 2675 EE 571 65

Example 3. 14 (Gambler’s Ruin Problem) Two gamblers play the game of “heads or tails, ” in which each time a fair coin lands heads up player A wins $1 from B, and each time it lands tails up, player B wins $1 from A. Suppose that player A initially has a dollars and player B has b dollars. If they continue to play this game successively, what is the probability that (a) A will be ruined; (b) the game goes forever with nobody winning? Sol: Ans: (a) b/(a+b) (b) 0 EE 571 66

Definition of Partition Let {B 1, B 2, …, Bn} be a set of nonempty subsets of the sample space S of an experiment. If the events B 1, B 2, …, Bn are mutually exclusive and , the set {B 1, B 2, …, Bn} is called a partition of S. B 5 B 1 B 2 S B 4 B 3 EE 571 67

Theorem 3. 4:Law of Total Prob. If {B 1, B 2, …, Bn} is a partition of the sample space of an experiment and P(Bi) > 0 for i = 1, 2, …, n, then for any event A of S, Pf: EE 571 68

Example 3. 15 Suppose that 80% of the seniors, 70% of the juniors, 50% of the sophomores, and 30% of the freshmen of a college use the library of their campus frequently. If 30% of all students are freshmen, 25% are sophomores, 25% are juniors, and 20% are seniors, what percent of all students use the library frequently? Sol: Ans: 0. 55 EE 571 69

Example 3. 16 Suppose that 16% of an insurance company’s automobile policyholders are male and under the age of 25, while 12% are females and under the age of 25. And Group Percentage of accidents Male under Female Between 25 Over 65 25 under 25 and 65 20% 8% 5% 10% Find the range of the percentages of this company’s policyholders who got involved in a car accident during the previous year. Sol: Ans: 7. 76%~11. 36% EE 571 70

Example 3. 17 An urn contains 10 white and 12 red chips. Two chips are drawn at random and, without looking at their colors, are discarded. What is the probability that a third chip drawn is red? Sol: Ans: 6/11 EE 571 71

3. 4 Baye’s Formula Theorem 3. 6 Let {B 1, B 2, …, Bn} is a partition of the sample space of an experiment. If for i = 1, 2, …, n, P(Bi) > 0, then for any event A of S with P(A) > 0 , If P(B) > 0 and P(Bc) > 0, then for any event A of S with P(A) > 0, EE 571 72

Example 3. 18 A study conducted 3 yrs ago, 82% of the people in a randomly selected sample were found to have good financial credit ratings, while the remaining 18% were found to have bad financial ratings. Current records of the people from the sample show that 30% of those with bad credit ratings have since improved their ratings to good, while 15% of those with good credit ratings have since changed to having a bad credit rating. What % of the people with good credit ratings now had bad ratings 3 yrs ago? Sol: Ans: 7. 2% EE 571 73

Example 3. 19 During a double homicide murder trial, based on circumstantial evidence alone, the jury becomes 15% certain that a suspect is guilty. DNA samples recovered from the murder scene are then compared with DNA samples extracted from the suspect. Given the size and conditions of the recovered samples, a forensic scientist estimates that the probability of the sample having come from someone other than the suspect is 10 -9. With this new information, how certain should the jury be of the suspect’s guilt? Sol: Ans: ~0. 999943 EE 571 74

Example 3. 20 Colonel Smith decides that the probability of an enemy attack against the left is 0. 2, against the center is 0. 5, and against the right is 0. 3. Since deception is normal as a preclude to battle, Colonel Brown, having intercepted the radio traffic, tells General Quick that if the enemy wanted to attack on the left, the probability is 0. 2. He tells the general that the corresponding probabilities for an attack on the center or the right are 0. 7 and 0. 1, respectively. How should General Quick use these two equally reliable staff members’ views to get the best probability profile for the forthcoming attack? Sol: EE 571 75

Example 3. 21 A box contains 7 red and 13 blue balls. 2 balls are selected at random and are discarded without their colors being seen. If a third ball is drawn randomly and observed to be red, what is the probability that both of the discarded balls were blue? Sol: EE 571 76

3. 5 Independence Definition Two events A and B are called independent if and only if P(AB) = P(A)P(B). If two events are not independent, they are called dependent. If A and B are independent, we say that {A, B} is an independent set of events. Note: Independent P(A|B)=P(A) EE 571 77

Independence of Three Events Definition The events A, B and C are called independent iff P(AB) = P(A)P(B), P(AC) = P(A)P(C), P(BC) = P(B)P(C), P(ABC) = P(A)P(B)P(C). If A, B and C are independent events, we say that {A, B, C} is an independent set of events. EE 571 78

Independence of n Events Definition The set of events { A 1 , A 2 , …, An } are called independent if and only if for every subset EE 571 79

Example 3. 22 In the experiment of tossing a fair coin twice, Let A and B be the events of getting heads on the first and second tosses, respectively. Are A and B independent? Sol: EE 571 80

Example 3. 23 In the experiment of drawing a card from an ordinary deck of 52 cards, let A and B be the events of getting a heart and an ace, respectively. Whether A and B are independent? Sol: EE 571 81

Example 3. 24 An urn contains 5 red and 7 blue balls. Suppose that 2 balls are selected at random and with replacement. Let A and B be the events that the first and the second balls are red, respectively. Are A and B independent? Sol: EE 571 82

Example 3. 25 In the experiment of selecting a random number from the set of natural numbers {1, 2, 3, …, 100 }, let A, B, and C denote the events that they are divisible by 2, 3, and 5, respectively. Are A, B, and C are independent? Sol: EE 571 83

Example 3. 26 A spinner is mounted on a wheel. Arcs A, B, and C, of equal length, are marked off on the wheel’s perimeter. In a game of chance, the spinner is flicked, and depending on whether it stops on A, B, or C, the player wins 1, 2, or 3 points, respectively. A player plays this game twice. Let E:he wins 1 point in the first game and any number of points in the second. A C F:he wins a total of 3 points in both game, G:he wins a total of 4 points in both games. Are E, F, and G are independent? B Sol: EE 571 84

Theorem 3. 6 If A and B are independent, then A and BC are independent as well. Pf: Corollary: If A and B are independent, then AC and BC are independent as well. Pf: EE 571 85

Example 3. 27 Dennis arrives at his office every day at a random time between 8: 00 Am and 9: 00 AM. Let A: he arrives 8: 15 AM and 8: 45 Am. B :he arrives between 8: 30 Am and 9: 00 AM, C :he arrives either between 8: 15 AM and 8: 30 AM or between 8: 45 AM and 9: 00 AM. Are A, B, and C are independent? Sol: EE 571 86

Example 3. 28 (Jailer’s Paradox) Alex, Ben, and Tim are held in a prison. The jailer is the only person who knows which of these 3 prisoners is condemned to death. Alex has written a letter to his fiancée. Just in case he is not one of the two who will be free, he wants to give the letter to a prisoner who goes free to deliver. So Alex asks the jailer to tell him the name of one of the two prisoners who will go free. The jailer refuses to give that information to Alex. Putting Alex aside, he argues that, if he reveals the name of a prisoner who will go free, then the probability of Alex dying increases from 1/3 to 1/2. He does not want to do that. Is it reasonable? EE 571 87

Example 3. 29 Let an experiment consists of throwing a die twice. Let A:the 2 nd throw the die lands 1, 2, or 5; B:the 2 nd throw it lands 4, 5, or 6; C:the sum of the two outcomes is 9. Are A, B, and C are independent Sol: EE 571 88

Example 3. 30 A regular tetrahedron is a body that has four faces and, if it is tossed, the probability that it lands on any faces is 1/4. Suppose that one face of a regular tetrahedron has 3 colors: red, green, and blue. The other 3 faces each has only one color: red, blue, and green, respectively. We throw the tetrahedron once, and let R:the faces it lands contains red; G:the faces it lands contains green; B:the faces it lands contains blue. Are R, G, and B are independent ? Sol: EE 571 89

Example 3. 31 We draw cards, one at a time, at random and successively from an ordinary deck of 52 cards with replacement. What is the probability that an ace appears before a face card? Sol: Ans: 1/4 EE 571 90
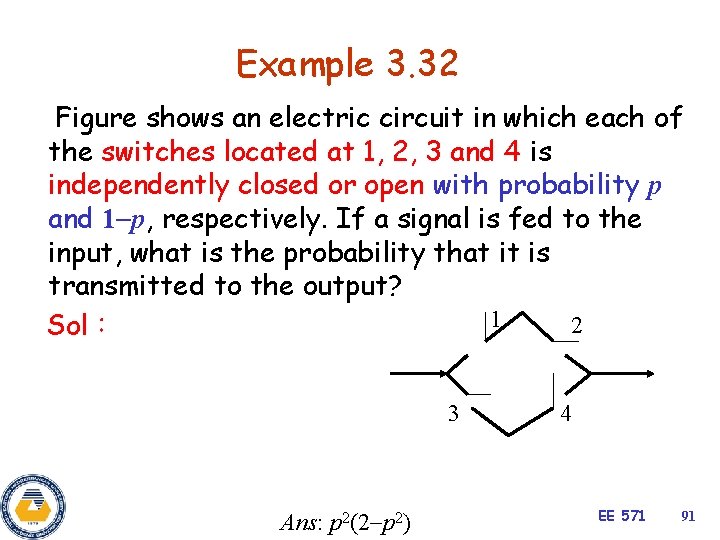
Example 3. 32 Figure shows an electric circuit in which each of the switches located at 1, 2, 3 and 4 is independently closed or open with probability p and 1 p, respectively. If a signal is fed to the input, what is the probability that it is transmitted to the output? 1 2 Sol: 3 Ans: p 2(2 p 2) 4 EE 571 91

Example 3. 33 Adam tosses a fair coin n+1 times, Andrew tosses the same coin n times. What is the probability that Adam gets more heads than Andrew? Sol: Ans: 1/2 EE 571 92
- Slides: 92