Parsing and Code Generation Set 24 Parser Construction

Parsing and Code Generation Set 24

Parser Construction Most of the work involved in constructing a parser is carried out automatically by a program, referred to as a compiler-compiler program, such as Yacc. To create a parser for a computer language, one constructs a description of the language, which is then employed as input to the compiler-compiler. This description of the language is in the form of a grammar for the language

Grammar 1 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. SENTENCE -> NOUNPHRASE VERB NOUNPHRASE -> the ADJECTIVE NOUNPHRASE -> the NOUN VERB -> pushed VERB -> helped ADJECTIVE -> pretty ADJECTIVE -> poor NOUN -> man NOUN -> boy NOUN -> cat

Grammar 1 is an example of a context-free grammar (the only kind we will deal with). The grammar consist of 10 productions e. g. production 3 is nounphrase -> the noun Here “nounphrase” is referred to as the lefthand side (lhs) and “the noun” is referred to as the righthand side (rhs)

The set of all lhs’s constitutes the set of nonterminals of the grammar. In this case they are: {SENTENCE, NOUNPHRASE, VERB, ADJECTIVE, NOUN} All the other symbols occurring in the grammar (i. e. in some rhs, but never as any lhs) are the terminals of the grammar. In this case {the, pushed, helped, pretty, poor, …}

The lhs of the first production is called the goal symbol, in this case “sentence”. A derivation of a string in the grammar is a list of strings starting with the goal symbol, in which each string, except the first, is obtained from the preceding one by applying a substitution of one of its symbols using one of the productions as a substitution rule

A string which has a derivation is said to be derivable. Derivable strings that consist entirely of terminal symbols are called sentences of the grammar. E. g. the man helped the poor boy is a sentence of Grammar 1. The set of all sentences of a grammar is called the language defined by the grammar

Grammar 1 (Cont. 1) Derivation of the sentence: 1. 2. 3. 4. 5. 6. 7. 8. ==> ==> "the man helped the poor boy“ SENTENCE (goal symbol) NOUNPHRASE VERB NOUNPHRASE (by Rule 1) the NOUN VERB NOUNPHRASE (Rule 3) the man VERB NOUNPHRASE (Rule 8) the man helped NOUNPHRASE the man helped the ADJECTIVE NOUN the man helped the poor boy (this derivation shows that "the man helped the poor boy“ is a sentence in the language defined by the grammar. )

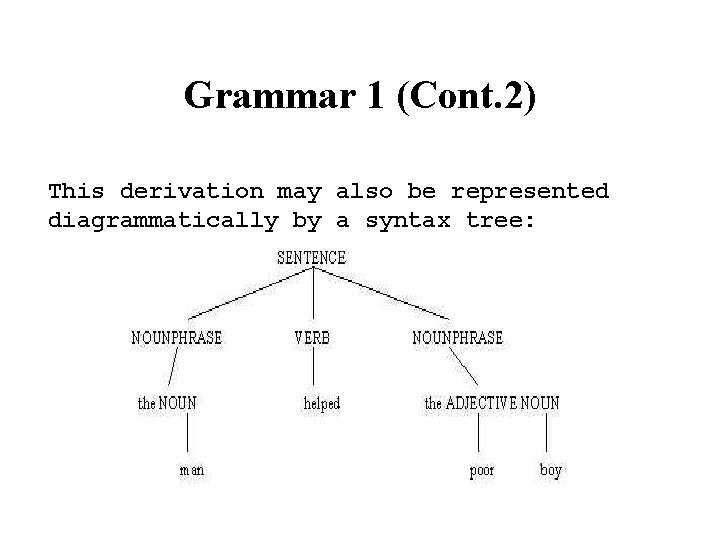
Grammar 1 (Cont. 2) This derivation may also be represented diagrammatically by a syntax tree:

Typical format of a grammar for a programming language PROGRAM -> PROGRAM STATEMENT PROGRAM -> STATEMENT -> ASSIGNMENT-STATEMENT -> IF-STATEMENT -> DO-STATEMENT. . . ASSIGNMENT-STATEMENT ->. . . IF-STATEMENT ->. . . DO-STATEMENT ->. . .

Grammar 2 A simple grammar for arithmetic statements 1. E -> E + T 2. E -> T 3. T -> T * a 4. T -> a

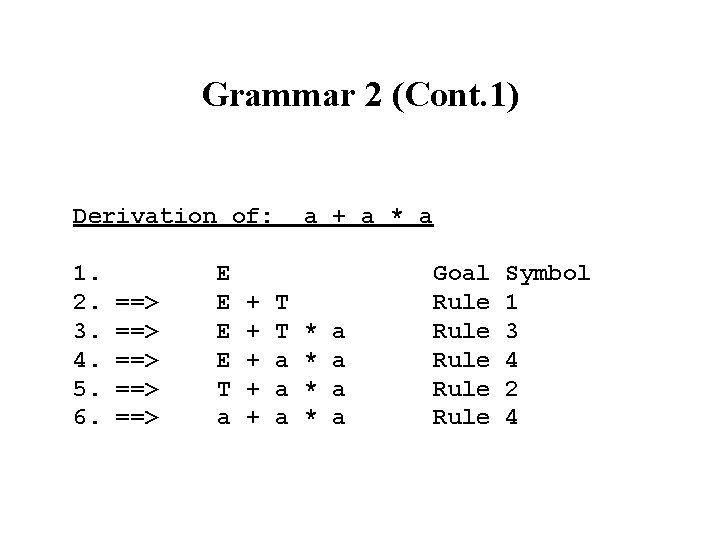
Grammar 2 (Cont. 1) Derivation of: 1. 2. 3. 4. 5. 6. ==> ==> ==> E E T a + + + a * a T T a a a * * a a Goal Rule Rule Symbol 1 3 4 2 4

Grammar 2 (Cont. 2) Derivation of: a + a * a written in reverse: 1. 2. 3. 4. 5. 6. a T E E + + + a a a T T * * a a Given sentential form Rule 4 in reverse Rule 2 in reverse Rule 4 Rule 3 in reverse Rule 1

Syntax Analysis -1 • One of the functions of syntax analysis (parsing) is to verify whether the source program is syntactically correct • The parser obtains a string of tokens from the scanner and verifies that the string can be generated by the grammar for the source language. (If not, the source program is not syntactically correct. )

Syntax Analysis -2 • There are many approaches to parsing, including both top-down and bottom-up approaches. • The LR parsing method discussed uses a bottomup approach (generating the derivation in reverse) • It constructs a rightmost derivation, in which at any step a production can only be applied to the rightmost nonterminal in the string involved.

LR Parsers -1 • An LR Parser uses an input buffer of the remaining source code to be read, a symbol stack, a state no. stack, and an action table to determine what action to take when the next symbol is read from the input buffer. • The parser reads tokens (a i) of the programming language grammar from the input buffer one at a time. • Using the combination of the state no. on top of the state stack and the current input symbol, ai, in the input buffer, the parser consults the action table to determine whether it should perform a transition or reduce action (as defined on the next slide)

LR Parsers -2 • When the action determined by the action table entry is make a transition to state s, the parser pushes the current input symbol ai onto the symbol stack and the new state no. s onto the state stack. • s is now the new top of the state no. stack, and • ai is the top of the symbol stack, and ai+1 is the new next input symbol. The remaining input to be processed is: ai+1. . . an -|) where the symbol -| represents the end of the source file

LR Parsers -3 If the action determined by the action table entry is reduce using production A -> α, the parser performs the following sequence of actions, where r is the no. of symbols in α : • Pops r symbols from the symbol stack and r states from the state stack. • Consults the action table so as to make a transition with respect to the nonterminal symbol A (the left hand side of the reduce production), and the current state no. now at the top of the state-no stack.

LR Parsers -4 • The remaining input remains unchanged (in contrast to transition actions). • Some of the reduce actions cause associated code to be generated.

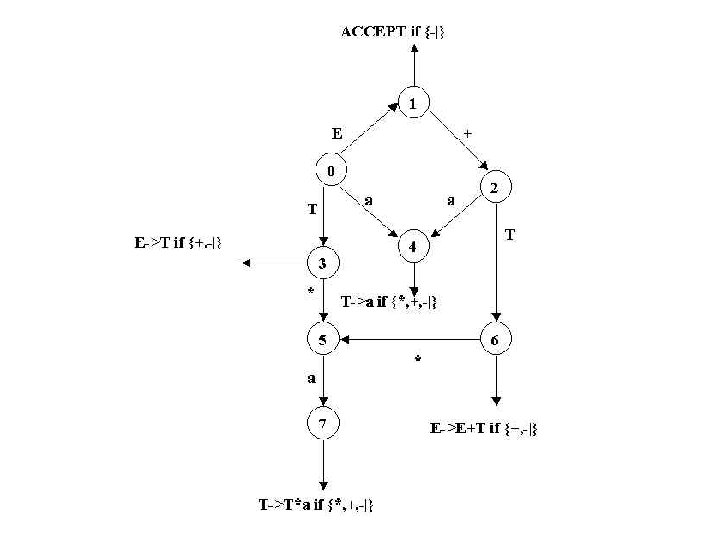
Example The following diagram graphically represents an action table generated for the grammar: E -> E + T | T T -> T * a | a It is called a parsing machine

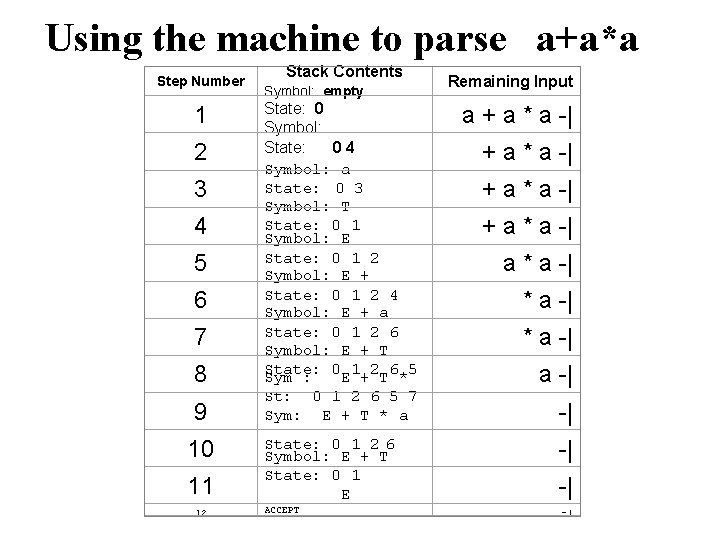
Using the machine to parse a+a*a Step Number 1 2 3 4 5 6 7 8 9 10 11 12 Stack Contents Symbol: empty State: 0 Symbol: State: 04 Symbol: a State: 0 3 Symbol: T State: 0 1 Symbol: E State: 0 1 2 Symbol: E + State: 0 1 2 4 Symbol: E + a State: 0 1 2 6 Symbol: E + T State: 0 1 2 6 5 Sym : E + T * St: 0 1 2 6 5 7 Sym: E + T * a Remaining Input a + a * a -| a * a -| -| State: 0 1 2 6 Symbol: E + T State: 0 1 E -| ACCEPT -| -|

Exercise 1. Supply a rightmost top-down derivation for a + a * a. 2. Supply a rightmost top-down derivation for a + a * a, this time without using Symbol Stack

Exercise (Cont. 1) Now, look at the derivation given in the parse example in the last second slide. First, cross out all the state numbers and also the end marker, then rewrite that step of the parse in this form: e. g. , Stack status: Remaining input Step 7 + a -| 0 E 1 + 2 T 6 is rewritten as: E + T + a and concatenated together becomes: E + T + a

Exercise (Cont. 2) Do this to every step of the derivation, then cross out any duplicates of a given step. Now compare the result with the top-down derivation you obtained above. How are these two sets of results related to each other? Note that the parse provides a "bottom-up" derivation --- which contains the same steps as the top-down derivation but in the reverse order.