Pareto Optimality in House Allocation Problems David Abraham

Pareto Optimality in House Allocation Problems David Abraham Computer Science Department Carnegie-Mellon University Katarína Cechlárová Institute of Mathematics PJ Safárik University in Košice David Manlove Department of Computing Science University of Glasgow Kurt Mehlhorn Max-Planck-Institut fűr Informatik Saarbrűcken Supported by Royal Society of Edinburgh/Scottish Executive Personal Research Fellowship and Engineering and Physical Sciences Research Council grant GR/R 84597/01

House Allocation problem (HA) n n Set of agents A={a 1, a 2, …, ar} Set of houses H={h 1, h 2, …, hs} n Each agent ai has an acceptable set of houses Ai H ai ranks Ai in strict order of preference n Example: n n n a 1 : h 2 a 2 : h 3 a 3 : h 4 a 4 : h 1 h 4 h 2 h 3 h 4 a 1 finds h 1 and h 2 acceptable a 3 prefers h 4 to h 3 Let n=r+s and let m=total length of preference lists 2
Applications n House allocation context: n n n Large-scale residence exchange in Chinese housing markets n Yuan, 1996 Allocation of campus housing in American universities, such as Carnegie-Mellon, Rochester and Stanford n Abdulkadiroğlu and Sönmez, 1998 Other matching problems: n n n US Naval Academy: students to naval officer positions n Roth and Sotomayor, 1990 Scottish Executive Teacher Induction Scheme Assigning students to projects 3
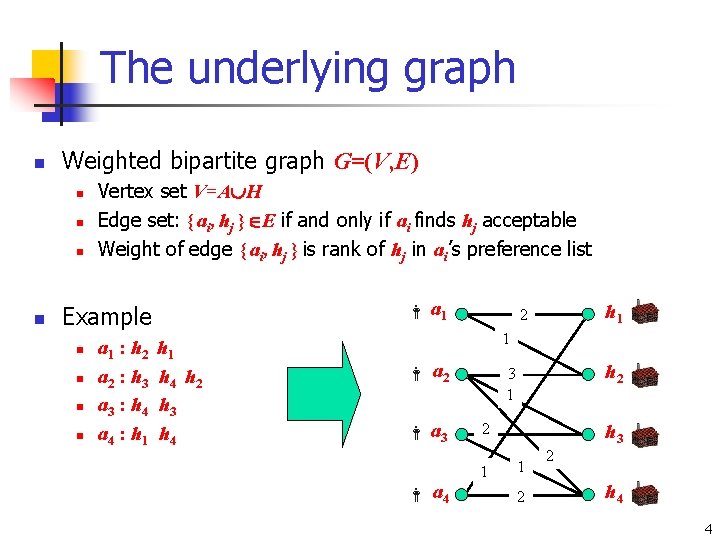
The underlying graph n Weighted bipartite graph G=(V, E) n n Vertex set V=A H Edge set: { ai, hj } E if and only if ai finds hj acceptable Weight of edge { ai, hj } is rank of hj in ai’s preference list a 1 Example n n a 1 : h 2 a 2 : h 3 a 3 : h 4 a 4 : h 1 h 4 h 2 h 3 h 4 h 1 2 1 a 2 a 3 a 4 h 2 3 1 2 1 h 3 1 2 2 h 4 4

The underlying graph n Weighted bipartite graph G=(V, E) n n Vertex set V=A H Edge set: { ai, hj } E if and only if ai finds hj acceptable Weight of edge { ai, hj } is rank of hj in ai’s preference list Example n n a 1 : h 2 a 2 : h 3 a 3 : h 4 a 4 : h 1 h 4 h 2 h 3 h 4 M(a 1)=h 1 M={(a 1, h 1), (a 2, h 4), (a 3, h 3)} a 1 h 1 2 1 a 2 a 3 a 4 h 2 3 1 2 1 h 3 1 2 2 h 4 5
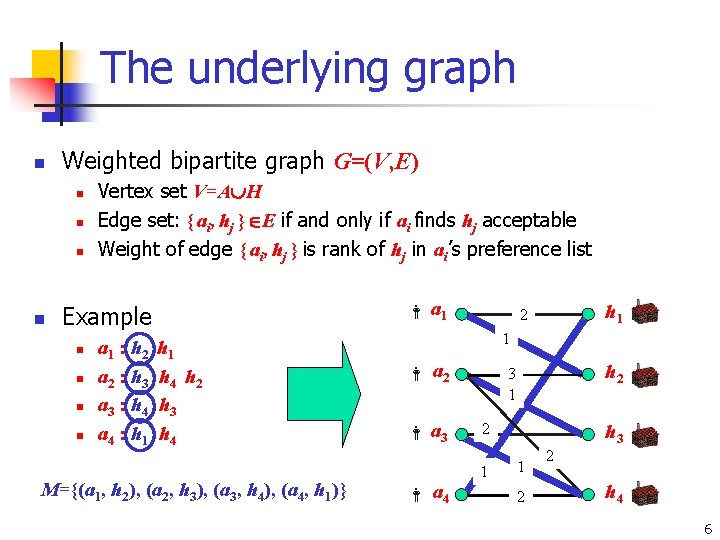
The underlying graph n Weighted bipartite graph G=(V, E) n n Vertex set V=A H Edge set: { ai, hj } E if and only if ai finds hj acceptable Weight of edge { ai, hj } is rank of hj in ai’s preference list a 1 Example n n a 1 : h 2 a 2 : h 3 a 3 : h 4 a 4 : h 1 h 4 h 2 h 3 h 4 M={(a 1, h 2), (a 2, h 3), (a 3, h 4), (a 4, h 1)} h 1 2 1 a 2 a 3 a 4 h 2 3 1 2 1 h 3 1 2 2 h 4 6
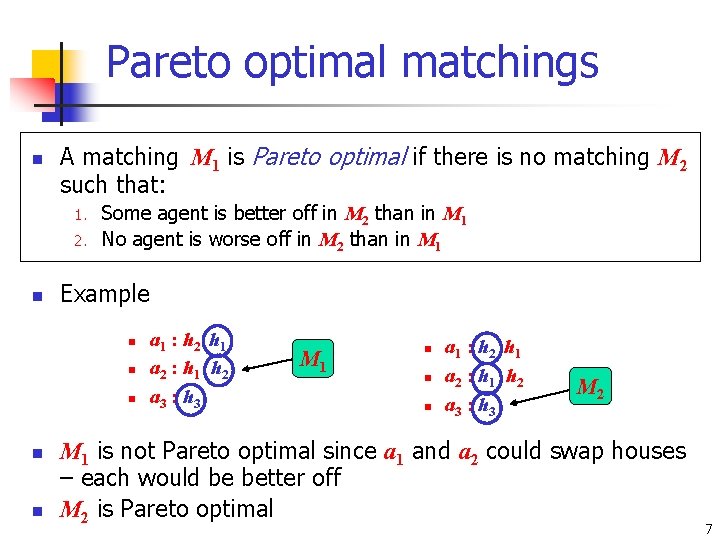
Pareto optimal matchings n A matching M 1 is Pareto optimal if there is no matching M 2 such that: 1. 2. n Some agent is better off in M 2 than in M 1 No agent is worse off in M 2 than in M 1 Example n n n a 1 : h 2 h 1 a 2 : h 1 h 2 a 3 : h 3 M 1 n n n a 1 : h 2 h 1 a 2 : h 1 h 2 a 3 : h 3 M 2 M 1 is not Pareto optimal since a 1 and a 2 could swap houses – each would be better off M 2 is Pareto optimal 7

Testing for Pareto optimality n n n A matching M is maximal if there is no agent a and house h, each unmatched in M, such that a finds h acceptable A matching M is trade-in-free if there is no matched agent a and unmatched house h such that a prefers h to M(a) A matching M is coalition-free if there is no coalition, i. e. a sequence of matched agents a 0 , a 1 , …, ar-1 such that ai prefers M(ai) to M(ai+1) (0 i r-1) n n n a 1 : h 2 a 2 : h 3 a 3 : h 4 a 4 : h 1 h 4 h 2 h 3 h 4 M is not maximal due to a 3 and h 3 Proposition: M is Pareto optimal if and only if M is maximal, trade-in-free and coalition-free 8

Testing for Pareto optimality n n n A matching M is maximal if there is no agent a and house h, each unmatched in M, such that a finds h acceptable A matching M is trade-in-free if there is no matched agent a and unmatched house h such that a prefers h to M(a) A matching M is coalition-free if there is no coalition, i. e. a sequence of matched agents a 0 , a 1 , …, ar-1 such that ai prefers M(ai) to M(ai+1) (0 i r-1) n n n a 1 : h 2 a 2 : h 3 a 3 : h 4 a 4 : h 1 h 4 h 2 h 3 h 4 M is not trade-in-free due to a 2 and h 3 Proposition: M is Pareto optimal if and only if M is maximal, trade-in-free and coalition-free 9
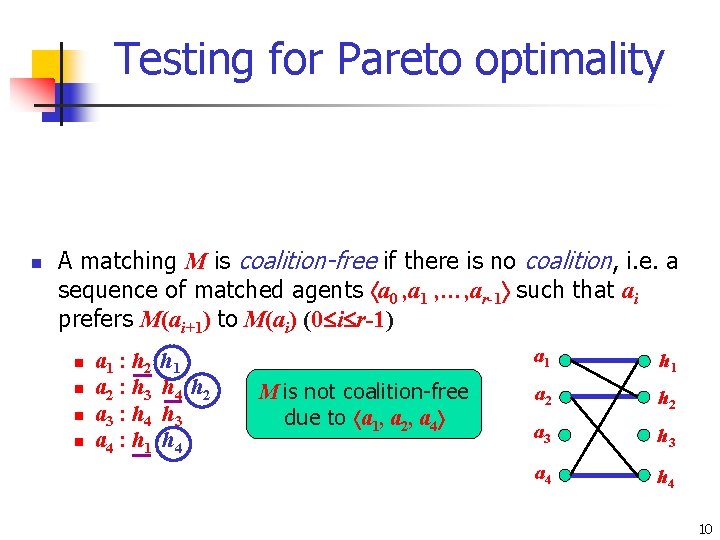
Testing for Pareto optimality n n n A matching M is maximal if there is no agent a and house h, each unmatched in M, such that a finds h acceptable A matching M is trade-in-free if there is no matched agent a and unmatched house h such that a prefers h to M(a) A matching M is coalition-free if there is no coalition, i. e. a sequence of matched agents a 0 , a 1 , …, ar-1 such that ai prefers M(ai+1) to M(ai) (0 i r-1) n n n a 1 : h 2 a 2 : h 3 a 3 : h 4 a 4 : h 1 h 4 h 2 h 3 h 4 M is not coalition-free due to a 1, a 2, a 4 a 1 h 1 a 2 h 2 a 3 h 3 4 Proposition: M is Pareto optimal if and only ifa. M is maximal, trade-in-free and coalition-free h 4 10

Testing for Pareto optimality n n n A matching M is maximal if there is no agent a and house h, each unmatched in M, such that a finds h acceptable A matching M is trade-in-free if there is no matched agent a and unmatched house h such that a prefers h to M(a) A matching M is coalition-free if there is no coalition, i. e. a sequence of matched agents a 0 , a 1 , …, ar-1 such that ai prefers M(ai+1) to M(ai) (0 i r-1) Lemma: M is Pareto optimal if and only if M is maximal, trade-in-free and coalition-free Theorem: we may check whether a given matching M is Pareto optimal in O(m) time 11

Finding a Pareto optimal matching n Simple greedy algorithm, referred to as the serial dictatorship mechanism by economists for each agent a in turn if a has an unmatched house on his list match a to the most-preferred such house; else report a as unmatched; n Theorem: The serial dictatorship mechanism constructs a Pareto optimal matching in O(m) time n n Abdulkadiroğlu and Sönmez, 1998 Example n n n a 1 : h 1 h 2 h 3 a 2 : h 1 h 2 a 3 : h 1 h 2 M 1={(a 1, h 1), (a 2, h 2)} M 2={(a 1, h 3), (a 2, h 2), (a 3, h 1)} n n n a 1 : h 1 h 2 h 3 a 2 : h 1 h 2 a 3 : h 1 h 2 12

Related work n Rank maximal matchings n Matching M is rank maximal if, in M 1. 2. n n n Irving, Kavitha, Mehlhorn, Michail, Paluch, SODA 04 A rank maximal matching is Pareto optimal, but need not be of maximum size Popular matchings n Matching M is popular if there is no other matching M’ such that: n n Maximum number of agents obtain their first-choice house; Subject to (1), maximum number of agents obtain their second-choice house; etc. more agents prefer M’ to M than prefer M to M’ Abraham, Irving, Kavitha, Mehlhorn, SODA 05 A popular matching is Pareto optimal, but need not exist Maximum cardinality minimum weight matchings n n n Such a matching M may be found in G in O( nmlog n) time Gabow and Tarjan, 1989 M is a maximum Pareto optimal matching 13

Faster algorithm for finding a maximum Pareto optimal matching n Three-phase algorithm with O( nm) overall complexity n Phase 1 – O( nm) time n n Find a maximum matching in G Classical O( nm) augmenting path algorithm n n Phase 2 – O(m) time n n Hopcroft and Karp, 1973 Enforce trade-in-free property Phase 3 – O(m) time n n Enforce coalition-free property Extension of Gale’s Top-Trading Cycles (TTC) algorithm n Shapley and Scarf, 1974 14

Phase 1 n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 Maximum matching M in G has size 8 M must be maximal No guarantee that M is trade-in-free or coalition-free 15

Phase 1 n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 Maximum matching M in G has size 9 M must be maximal No guarantee that M is trade-in-free or coalition-free 16
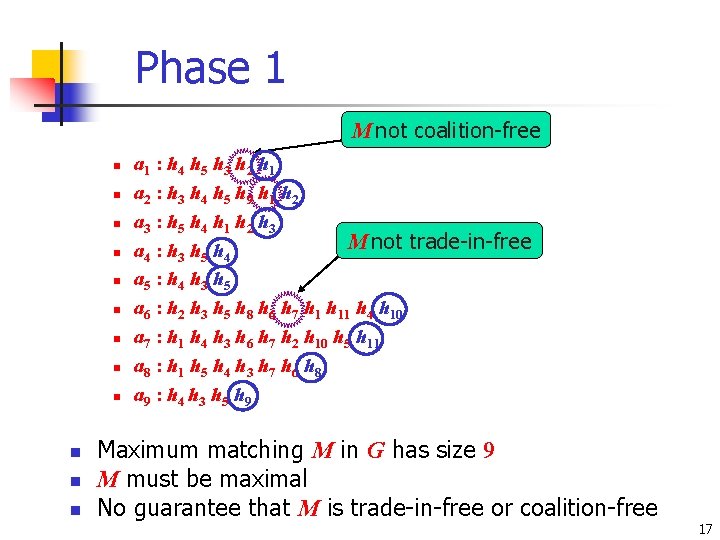
Phase 1 M not coalition-free n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 M not trade-in-free a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 Maximum matching M in G has size 9 M must be maximal No guarantee that M is trade-in-free or coalition-free 17

Phase 2 outline n Repeatedly search for a matched agent a and an unmatched house h such that a prefers h to h’=M(a) Promote a to h h’ is now unmatched n Example n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 18

Phase 2 outline n Repeatedly search for a matched agent a and an unmatched house h such that a prefers h to h’=M(a) Promote a to h h’ is now unmatched n Example n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 19

Phase 2 outline n Repeatedly search for a matched agent a and an unmatched house h such that a prefers h to h’=M(a) Promote a to h h’ is now unmatched n Example n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 20

Phase 2 outline n Repeatedly search for a matched agent a and an unmatched house h such that a prefers h to h’=M(a) Promote a to h h’ is now unmatched n Example n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 21

Phase 2 termination n Once Phase 2 terminates, matching is trade-in-free With suitable data structures, Phase 2 is O(m) Coalitions may remain… n n n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 22

Phase 3 outline n n Build a path P of agents (represented by a stack) Each house is initially unlabelled Each agent a has a pointer p(a) pointing to M(a) or the first unlabelled house on a’s preference list (whichever comes first) Keep a counter c(a) for each agent a (initially c(a)=0) n n This represents the number of times a appears on the stack Outer loop iterates over each matched agent a such that p(a) M(a) Initialise P to contain agent a Inner loop iterates while P is nonempty n n Pop an agent a’ from P If c(a’)=2 we have a coalition (CYCLE) n n Else if p(a’)=M(a’) we reach a dead end (BACKTRACK) n n Remove by popping the stack and label the houses involved Label M(a’) Else add a’’ where p(a’)=M(a’’) to the path (EXTEND) n n Push a’ and a’’ onto the stack Increment c(a’’) 23

Phase 3 termination n Once Phase 3 terminates, matching is coalition-free n n n a 1 : h 4 h 5 h 3 h 2 h 1 a 2 : h 3 h 4 h 5 h 9 h 1 h 2 a 3 : h 5 h 4 h 1 h 2 h 3 a 4 : h 3 h 5 h 4 a 5 : h 4 h 3 h 5 a 6 : h 2 h 3 h 5 h 8 h 6 h 7 h 11 h 4 h 10 a 7 : h 1 h 4 h 3 h 6 h 7 h 2 h 10 h 5 h 11 a 8 : h 1 h 5 h 4 h 3 h 7 h 6 h 8 a 9 : h 4 h 3 h 5 h 9 Phase 3 is O(m) Theorem: A maximum Pareto optimal matching can be found in O( nm) time 24

Initial property rights n Suppose A’ A and each member of A’ owns a house initially n n n n For each agent a A’, denote this house by h(a) Truncate a’s list at h(a) Form matching M by pre-assigning a to h(a) Use Hopcroft-Karp algorithm to augment M to a maximum cardinality matching M’ in restricted HA instance Then proceed with Phases 2 and 3 as before Constructed matching M’ is individually rational If A’=A then we have a housing market n TTC algorithm finds the unique matching that belongs to the core n n Shapley and Scarf, 1974 Roth and Postlewaite, 1977 25

Minimum Pareto optimal matchings n Theorem: Problem of finding a minimum Pareto optimal matching is NP-hard n n n Result holds even if all preference lists have length 3 Reduction from Minimum Maximal Matching Problem is approximable within a factor of 2 n n Follows since any Pareto optimal matching is a maximal matching in the underlying graph G Any two maximal matchings differ in size by at most a factor of 2 n Korte and Hausmann, 1978 26

Interpolation of Pareto optimal matchings n n n Given an HA instance I, p-(I) and p+(I) denote the sizes of a minimum and maximum Pareto optimal matching Theorem: I admits a Pareto optimal matching of size k, for each k such that p-(I) k p+(I) Given a Pareto optimal matching of size k, O(m) algorithm constructs a Pareto optimal matching of size k+1 or reports that k=p+(I) 1 a n n n Based on assigning a vector r 1, …, rk to an augmenting path P= a 1, h 1, …, ak, hk where ri=rankai(hi) Examples: 1, 3, 2 1, 2, 2 Find a lexicographically smallest augmenting path 1 a 3 1 2 a 4 1 2 a 2 h 1 h 2 h 3 h 4 h 5 27

Open problems Finding a maximum Pareto optimal matching n Ties in the preference lists n n Solvable in O( nmlog n) time Solvable in O( nm) time? n One-many case (houses may have capacity >1) n Non-bipartite case n Solvable in O( (n (m, n))mlog 3/2 n) time n n D. J. Abraham, D. F. Manlove Pareto optimality in the Roommates problem Technical Report TR-2004 -182 of the Computing Science Department of Glasgow University Solvable in O( nm) time? 28
- Slides: 28